GNN2.1 DeepWalk (PaperReading)

GNN学习笔记

GNN从入门到精通课程笔记

2.1 DeepWalk (PaperReading)

DeepWalk: Online Learning of Social Representations (KDD’ 14)

Introduction

• Unsupervised feature learning
• Input: graph; Output: Latent representation
• GNN basic dataset: Zachary’s Karate network
• one-hot encoding-Sparse; embedding-dense
• Heterogeneous graphs: graphs that have nodes and edges of different types
• Relational classification: aims to include relations among entities into the classification process (在一个图中标注一些节点预测其他节点)

Contribution

• DeepWalk used a different approach to capture the network topology information. Build robust representations that are suitable for statistical modeling
• Multi-label classification tasks
• Scalability (parallel implementation)

Problem Definition

• G = (V,E) V: vertices, E: edge, E=(V*V) 邻接矩阵
• G_L = (V, E, X, Y), X \in R^{|V|*S}, S = the size of the feature space for each attribute vector, Y \in R^{|V|*y}, y = the set of labels

Learning Social Representations

• (short) Random walks
  • Easy to parallelize
  • No need for global recomputation.
• Language modeling
  • We present a generalization of language modeling to explore the graph through a stream of short random walks.
    • Pr(v_i | (v_1,v_2,…,v_{i-1})): language modeling
  • the prediction problem
    • minimize_\Phi -logPr({v_{i-w},…,v_{i+w}}\v_i | \Phi(v_i)): skipgram(节点没有顺序)

Method

• DeepWalk = Random walks + Language modeling
• Language model: corpus + vocalulary
  • Deepwalk: corpus = short truncated random walks; vocalulary = V
• Algorithm
  
• SkipGram:
  
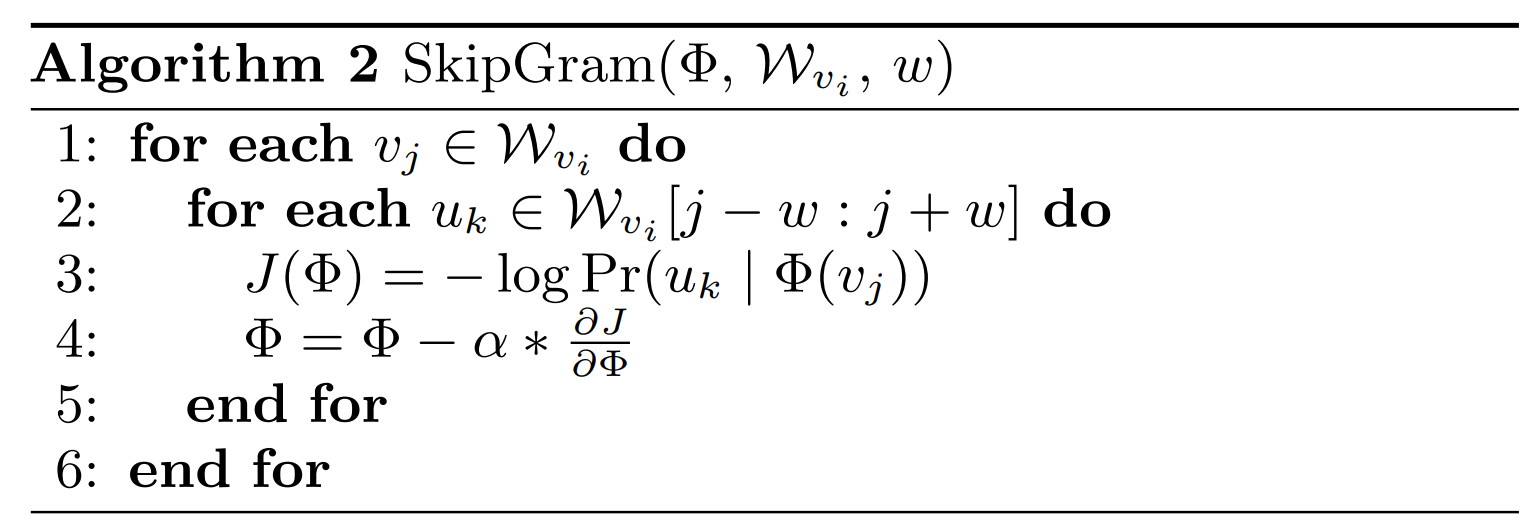
  • Pr(v_i | (v_1,v_2,…,v_{i-1})) = \Pi^{i+w}_{j=i-w;j!=i} Pr(v_j|\Phi(v_i))
• Hierarchical Softmax
  
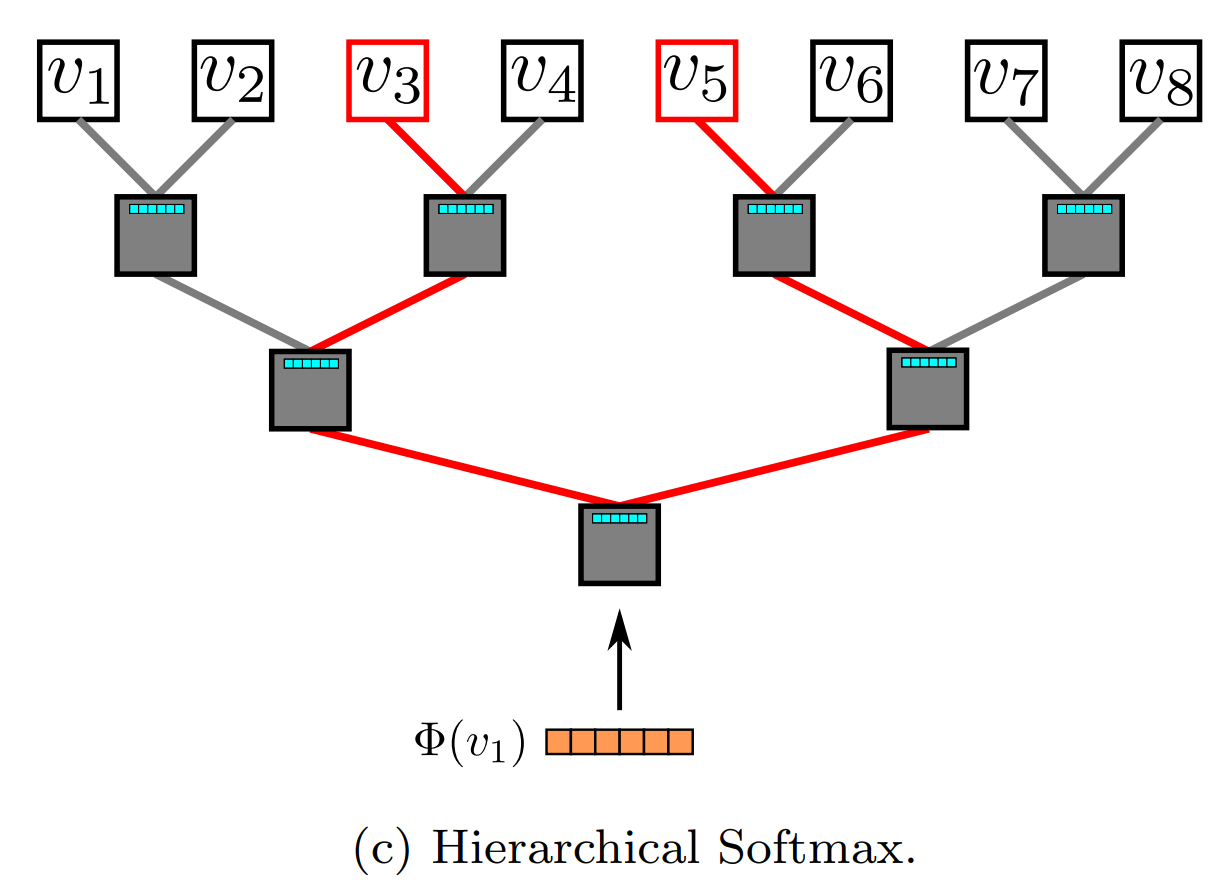
• The model parameter set is \theta = {\Phi,\Kai}
• Parallelizability
• Algorithm Variants
  • Streaming: without knowledge of the entire graph
  • Non-random walks

Experiments

• Datasets: BlogCatalog, Flickr, YouTube
• Metrics:
  • sample a portion of the labeled nodes(TR)
  • Macro-F1, Micro-F1
• Results: TR越小，DeepWalk表现地越突出

Conclusion

• Language modeling is actually sampling from an unobservable language graph.
• Insights obtained from modeling observable graphs may in turn yield improvements to modeling unobservable ones.