GNN学习笔记

GNN从入门到精通课程笔记

2.5 SDNE (KDD ‘16)

  • Structural Deep Network Embedding (KDD ‘16)

Abstract

  • semi-supervised deep model
  • exploit the first-order and second-order proximity jointly to preserve the network structure.
  • preserve both the local and global network structure and is robust to sparse networks.

Introduction

  • Challenges of learning network representations
    • High non-linearity
    • Structure-preserving
    • Sparsity
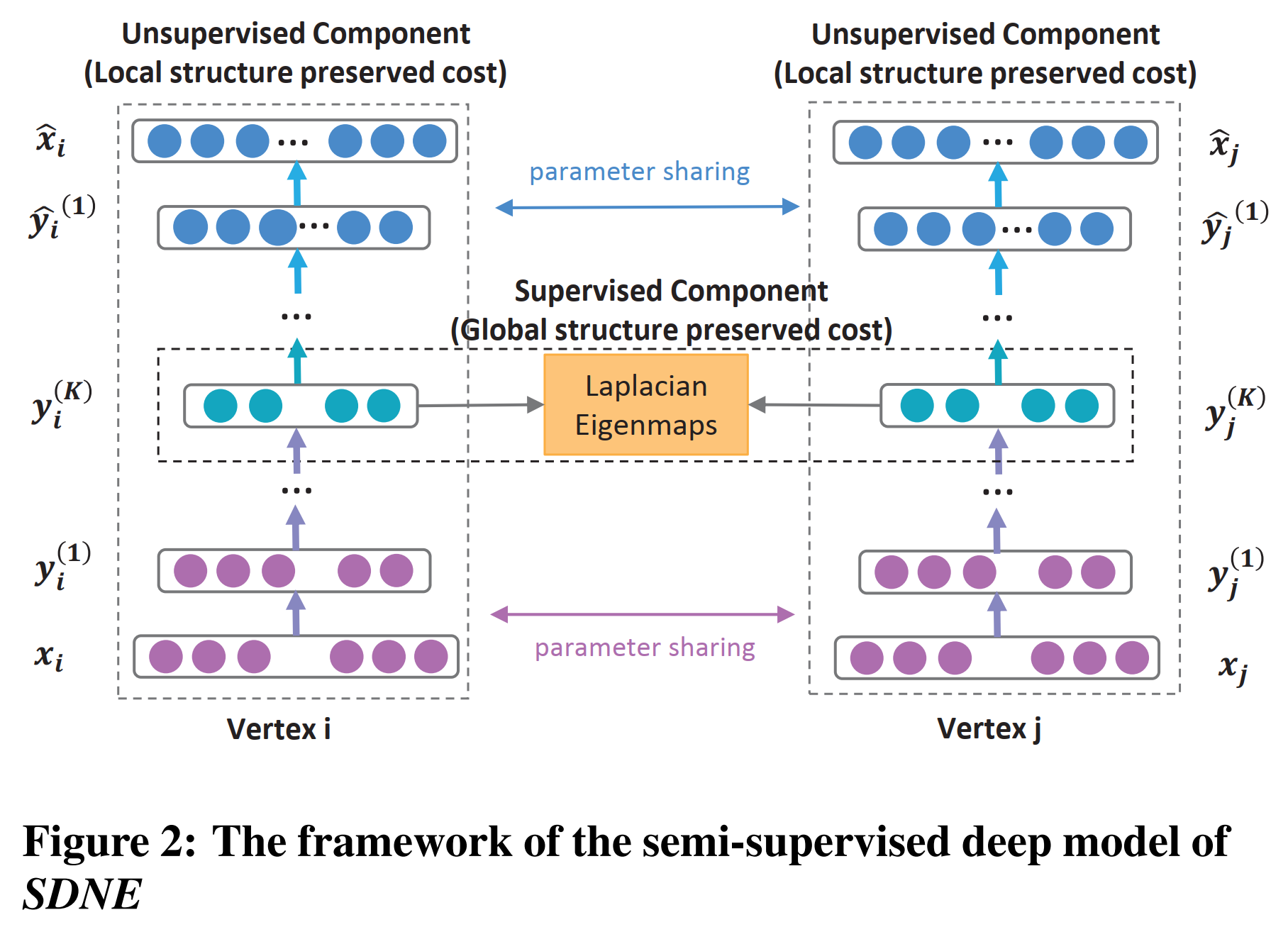
  • Semi-supervised architecture
    • The unsupervised component reconstructs the second-order proximity to preserve the global network structure.
    • The supervised component exploits the first-order proximity as the supervised information to preserve the local network structure.

Structure Deep Network Embedding

  • Definition
    • First-Order Proximity: The first-order proximity describes the pairwise proximity between vertexes.
    • Second-Order Proximity: The second-order proximity between a pair of vertexes describes the proximity of the pair’s neighborhood structure.
  • Model
    • Adjacency matrix S: s_i = {s_{i,j}}_{j=1}^n, s_{i,j} > 0 IFF there exists a link between v_i and v_j.
    • Autoencoder: unsupervised -> second-order proximity

      • Problem: the links between vertexes do indicate their similarity but no links do not necessarily indicate their dissimilarity.
      • first-order proximity
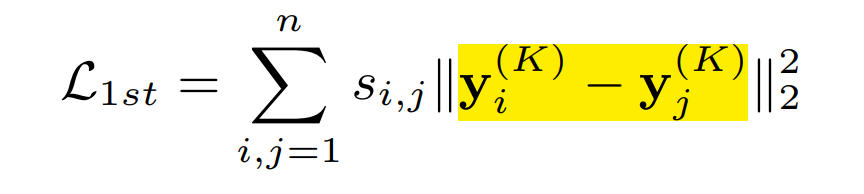
      • objective function
      • New vertexes
        • If its connection to the existing vertexes is known, we can obtain its adjacency vector x and simply feed the x into our model and use the trained parameters to get the representations.
  • Implement
    • 深入理解AutoEncoder及其实现方法:
      • # Node = n, Adjacency Matrix S[n*n]
      • Input batch: [bz,n]
      • Encoder:
        • encoder1 = [n, e1] outpupt1 = [bz,n][n,e1] = [bz,e1]
        • encoder2 = [e1, embed] output2 = [bz, e1][e1, embed] = [bz,embed]
      • Decode:
        • decoder1 = [embed, d1] output3 = [bz, embed] [embed, d1] = [bz, d1]
        • decoder2 = [d1, n] output = [bz, d1][d1, n] = [bz, n]
      • Loss
        • L1_Loss: torch.sum(adj * (embed*embed - 2*torch.mm(embed,embed.t)) + embed*embed.t)
          • 矩阵乘法和转置运算来计算一个矩阵的平方和(L2 Norm)
        • L2_Loss: torch.sum(((adj_batch - output) * b) * ((adj_batch - output) * b))
        • L2-norm regularizer: \Sigma(torch.sum(torch.abs(param)) + args.nu2 * torch.sum(param * param))