GNN学习笔记

GNN从入门到精通课程笔记

3.1 GCN (ICLR ‘17)

  • Semi-supervised Classification with Graph Convolutional Network (ICLR ‘17)

Abstract

  • We present a scalable approach for semi-supervised learning on graph-structured data that is based on an efficient variant of convolutional neural networks which operate directly on graphs.
  • We motivate the choice of our convolutional architecture via a localized first-order approximation of spectral graph convolutions.
  • Our model scales linearly in the number of graph edges and learns hidden layer representations that encode both local graph structure and features of nodes.

Introduction

  • Graph-based semi-supervised learning: classifying nodes in a graph network, where labels are only available for a small subset of nodes.
  • f(X,A)
    • X: a matrix of node feature vectors $X_i$
    • A: an adjacency matrix
  • Contribution:
    • a simple and well-behaved layer-wise propagation rule for neural network models which operate directly on graphs
    • how this form of a graph-based neural network model can be used for fast and scalable semi-supervised classification of nodes in a graph

Fast Approximate convolutions on graphs

  • Basic Appoach
    • Average neighbor messages and apply a neural network
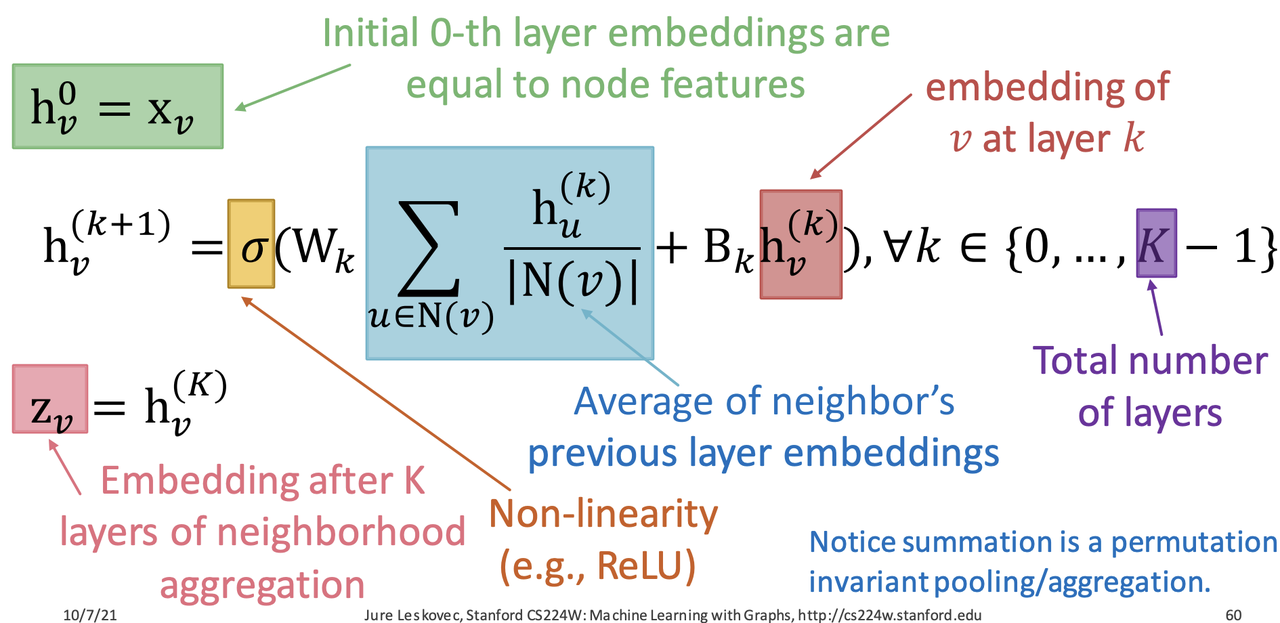
    • Matrix Formulation: $H^{k+1} = \sigma(\tilde{A}H^kW_k^T+H^kB_k^T)$
      • $\tilde{A} = D^{-1}A$: row normalized matrix
      • $\tilde{A}H^kW_k^T$ : neighborhood aggregation
      • $H^kB_k^T$: self transformation
  • Improvement
    • The normalized adjacency matrix: $\tilde{A} = D^{-1/2}(A)D^{-1/2}$
    • $\tilde{A} = A + A_N$, $\tilde{D}_{ii} = \Sigma{\tilde{A}_{ij}}$
      • H: features

Semi-supervised Node Classification

  • adjacency matrix: $\hat{A} = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{\frac{1}{2}}$
  • Two-layer GCN for semi-supervised node classification

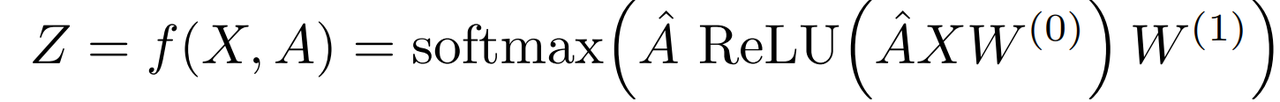
Experiments

  • scales linearly in the number of graph edges

Implementation

  • [1] Kipf, Thomas N., and Max Welling. “Semi-supervised classification with graph convolutional networks.” arXiv preprint arXiv:1609.02907 (2016).
  • [2] https://github.com/tkipf/pygcn
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
# graph preprocess
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj) # build symmetric adjacency matrix [directed graph -> undirected graph]
adj = normalize(adj + sp.eye(adj.shape[0])) #\Tilde{D^{-1}}(A+I_N)

def normalize(mx): #D^{-1}A
    """Row-normalize sparse matrix"""
    rowsum = np.array(mx.sum(1))
    r_inv = np.power(rowsum, -1).flatten()
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)
    mx = r_mat_inv.dot(mx)
    return mx


# GNN Layer
class GraphConvolutionLayer(Module):
    """
    Simple GCN layer, similar to https://arxiv.org/abs/1609.02907
    """

    def __init__(self, in_features, out_features, bias=True):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = Parameter(torch.FloatTensor(in_features, out_features))
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)

    def forward(self, input, adj):
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support) # sparse matrix multiplication
        if self.bias is not None:
            return output + self.bias
        else:
            return output
            
# Node classification
class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout):
        super(GCN, self).__init__()

        self.gc1 = GraphConvolutionLayer(nfeat, nhid)
        self.gc2 = GraphConvolutionLayer(nhid, nclass)
        self.dropout = dropout

    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.gc2(x, adj)
        return F.log_softmax(x, dim=1)
        
def train():
    model.train()
    optimizer.zero_grad()
    output = model(features, adj)
    loss_train = F.nll_loss(output[idx_train], labels[idx_train])
    loss_train.backward()
    optimizer.step()
    
def test():
    model.eval()
    output = model(features, adj)
    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])