ZKP学习笔记

ZK-Learning MOOC课程笔记

Lecture 1: Introduction and History of ZKP (Shafi Goldwasser)

1.3 Definitions of Zero Knowledge Interactive Proofs

  • Interactive Proofs: Notation
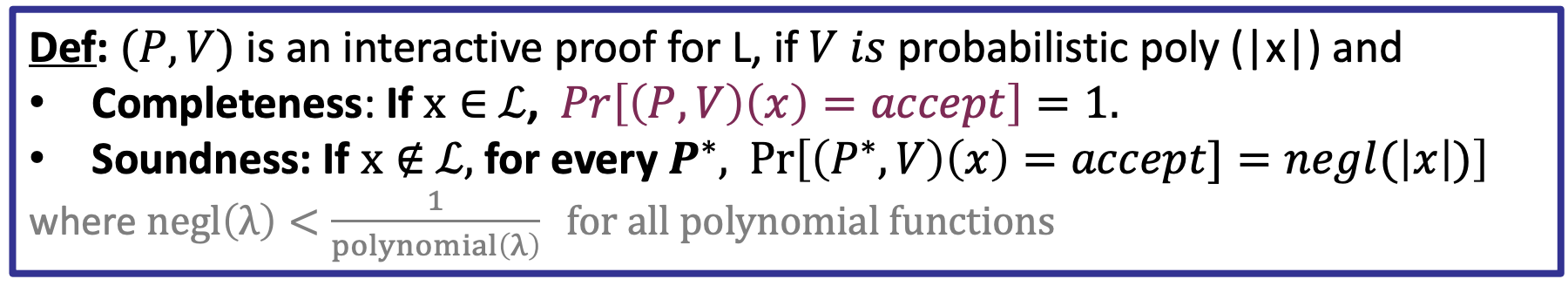
  • What is zero-knowledge？
    • For true Statements What the verifier can compute after the interaction = What the verifier could have computed before interaction
    • The Simulation Paradigm
      • V’s view gives him nothing new, if he could have simulated it its own s.t ‘simulated view’ and ‘real-view’ are computationally-Indistinguishable
      • Computational Indistinguishability: For all distinguisher algorithms D, even after receiving a polynomial number of samples from $D_b$, Prob[D guesses b]<1/2+negl(k)
    • Definition
    • Def: (P,V) is a zero-knowledge interactive protocol if it is complete, sound and zero-knowledge
    • What if V is NOT HONEST?
    • Perfect Zero Knowledge
      • verifier’s view can be exactly efficiently simulated ‘Simulated views’ = ‘real views’
  • Working through a Simulation for QR Protocol
    • (Honest Verifier) Perfect Zero Knowledge
    • Perfect Zero Knowledge: for all V*