ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 2 Overview of Modern SNARK Constructions (Dan Boneh)
- What is a zk-SNARK (intuition)
- SNARK is a succinct proof that a certain statement is true.
- The proof is short and fast to verify
- zk-SNARK: the proof reveals nothing about the privacy of a message
- Babai-Fortnow-Levin-Szegedy 1991: In this setup, a single reliable PC can monitor the operation of a herd of supercomputers working with unreliable software.
- Applications
- Blockchain
- Scalability: proof-based Rollups (zkRollup)
- Bridging blockchains: proof of consensus (zkBridge)
- Private Tx on a public blockchain: zk proof that a private Tx is valid (Tornado cash, Zcash, IronFish, Aleo)
- Compliance: Proof that a private Tx is compliant with banking laws (Espresso); Proof that an exchange is solvent in zero-knowledge (Raposa)
- C2PA: a standard for content provenance, T. Datta, 2022 (fighting disinformation)
- Solve the problem: post-processing (resized photo)

- Solve the problem: post-processing (resized photo)
- A. Naveh and E. Tromer, “PhotoProof: Cryptographic Image Authentication for Any Set of Permissible Transformations,” 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 2016, pp. 255-271, doi: 10.1109/SP.2016.23.
- Blockchain
- Review: Arithmetic circuits

- Input: n elements in finite field
- Output: an element in finite field
- Structured vs. Unstructured circuits
- An unstructured circuit: a circuit with arbitrary wires

- M: Micro processor
- Some SNARK techniques only apply to structured circuits
- An unstructured circuit: a circuit with arbitrary wires
- NARK: Non-interactive ARgument of Knowledge
- A preprocessing NARK is a triple (S, P, V)
- S(C) -> public parameters (pp,vp) for prover and verifier
- P(pp, x, w) -> proof $\Pi$
- V(vp, x, $\Pi$) -> accept or reject
- requirements (informal)

- A trivial NARK: $\Pi$ = w
- SNARK: a Succinct ARgument of Knowledge
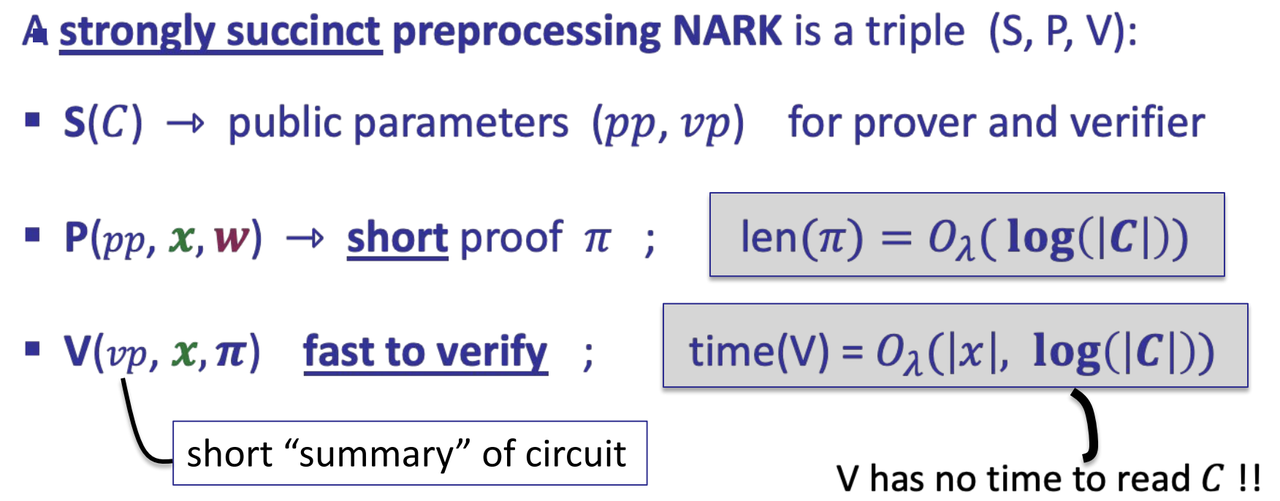
- The trivial NARK is not a SNARK
- Types of preprocessing Setup
- Setup of a Circuit C: S(C, r)-> public parameters (pp, vp)

- for a circuit with ≈$2^{20}$ gates
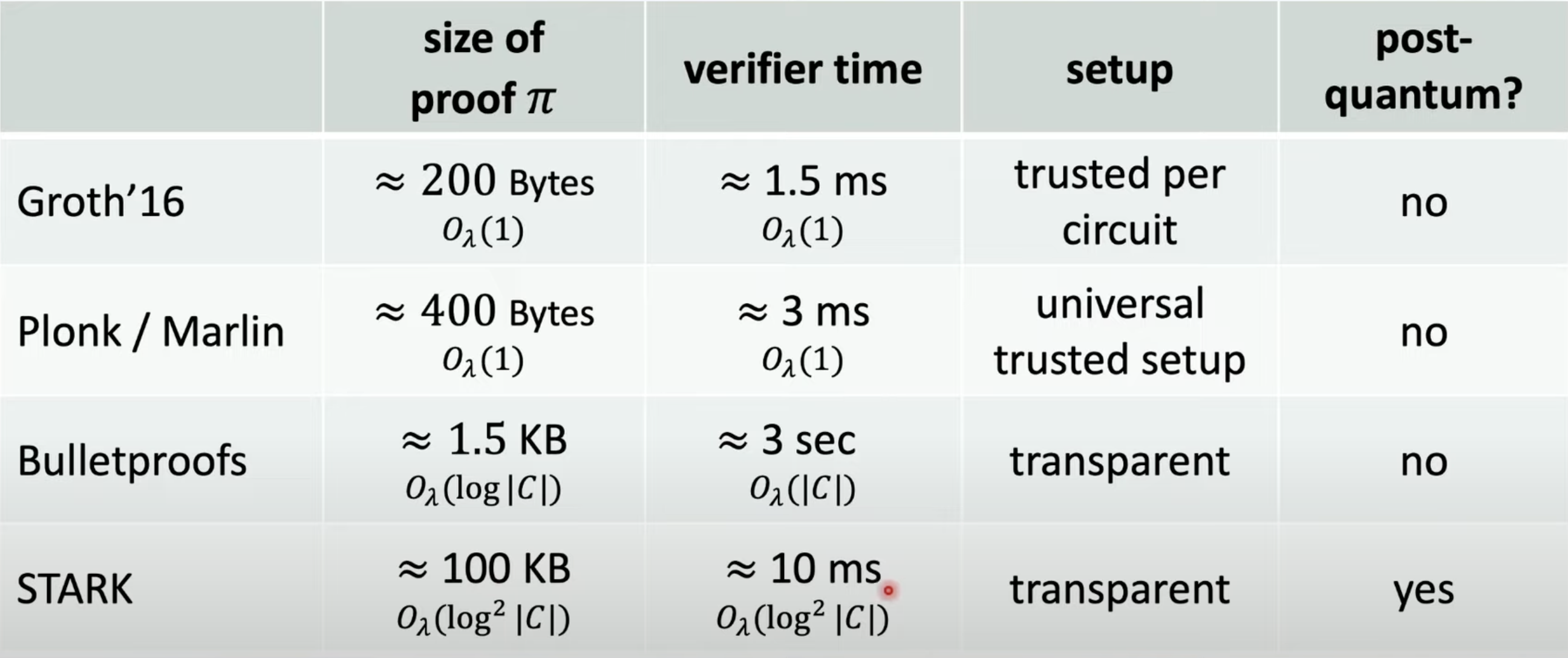
- Setup of a Circuit C: S(C, r)-> public parameters (pp, vp)
- Definitions: knowledge soundness

- Building an efficient SNARK: General paradigm
- Step 1: A functional commitment scheme (cryptographic object)
- Step 2: A compatible interactive oracle proof (IOP)
- Review: commitment scheme
- commit(m,r) -> com (r chosen at random)
- verify(m, com, r) -> accept or reject
- Properties (Informat):
- Binding: cannot produce com and two valid openings
- Hiding: com reveals nothing about committed data
- Committing to a function: syntax

- Four important functional commitments

- Polynomial commitments

- Examples
- Using bilinear groups: KZG10(trusted setup), Dory’20
- Using hash function only: based on FRI
- Using elliptic curve: Bulletproofs
- Using groups of unknown order: Dark’20
- trivial commitment scheme

- Proof $\Pi$ is not succint: prove size and verification time are all linear to d
- It is not a polynomial commitment
- A useful observation
- Zero test

- Equality test

- The equality test protocol
- Interactive protocol
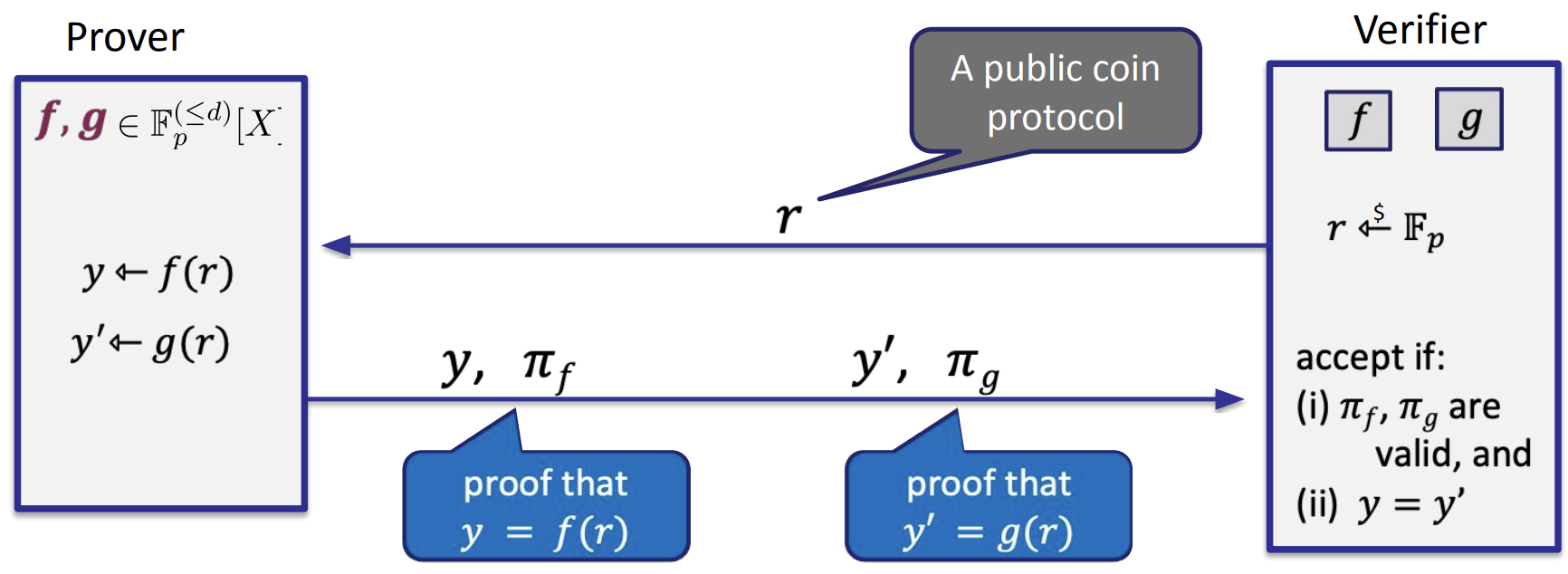
- Making it a SNARK (non-interactive)
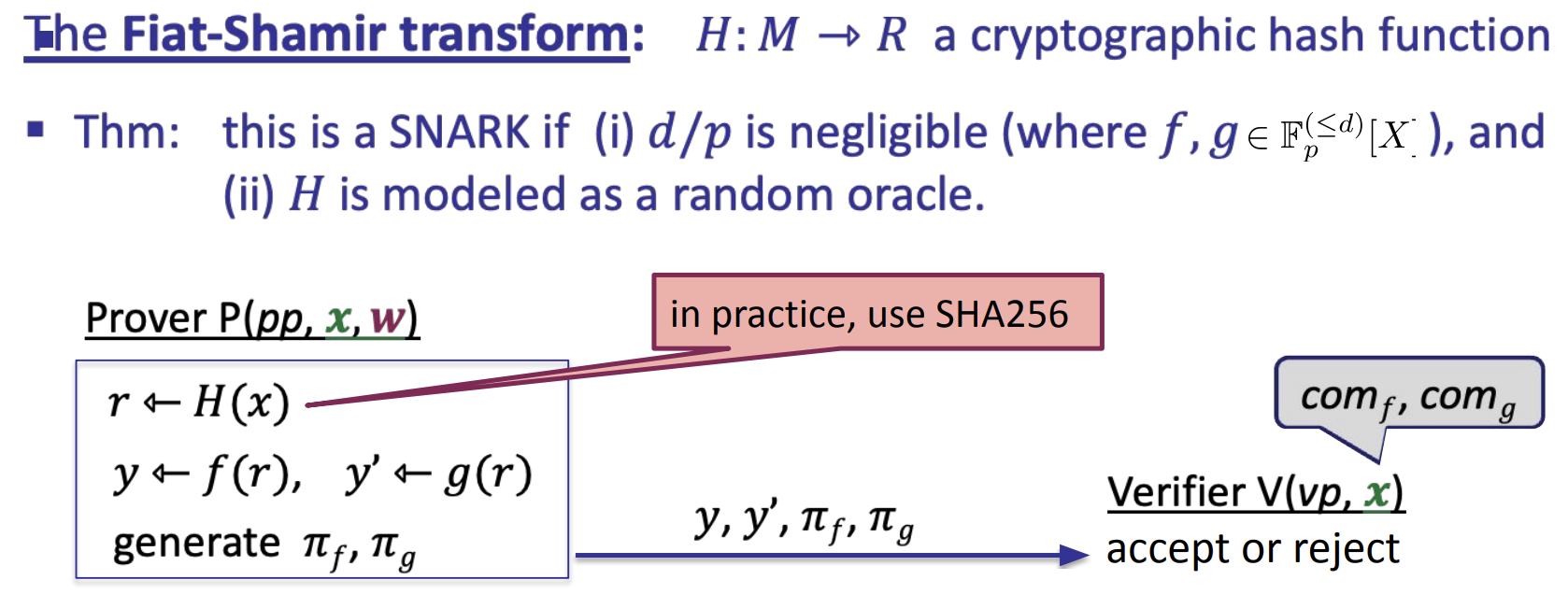
- The Fiat-Shamir transform
- Interactive protocol
- Zero test
- F-IOP
- boost functional commitment -> SNARK for general circuits

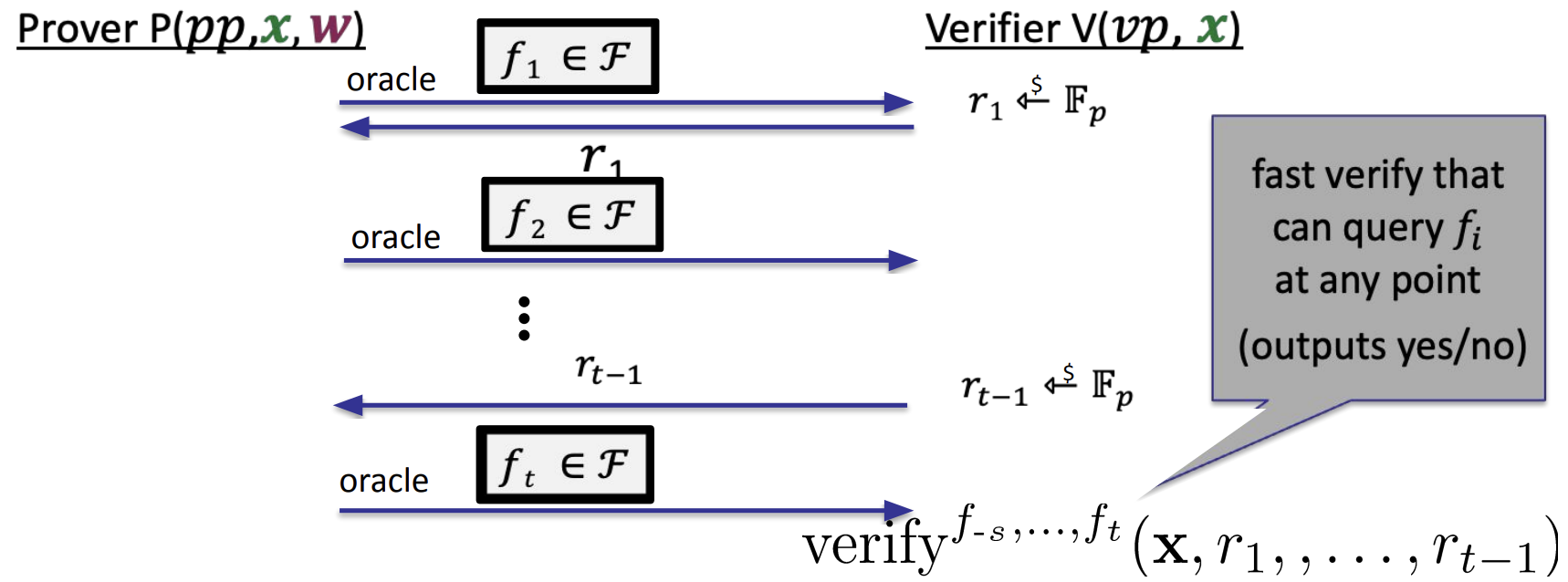
- Just like the SumCheck Protocol
- boost functional commitment -> SNARK for general circuits
- The IOP Zoo
- Poly-IOP: Sonic, Marlin, Plonk,… (+Poly-Commit)
- Multilinear-IOP: Spartan, Clover, Hyperplonk,… (+Multilinear-Commit)
- Vector-IOP: STARK, Breakdown, Orion,… (+Merkle-Commit)