ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 3: Programming ZKPs (Guest Lecturers: Pratyush Mishra and Alex Ozdemir)
- Using ZKP
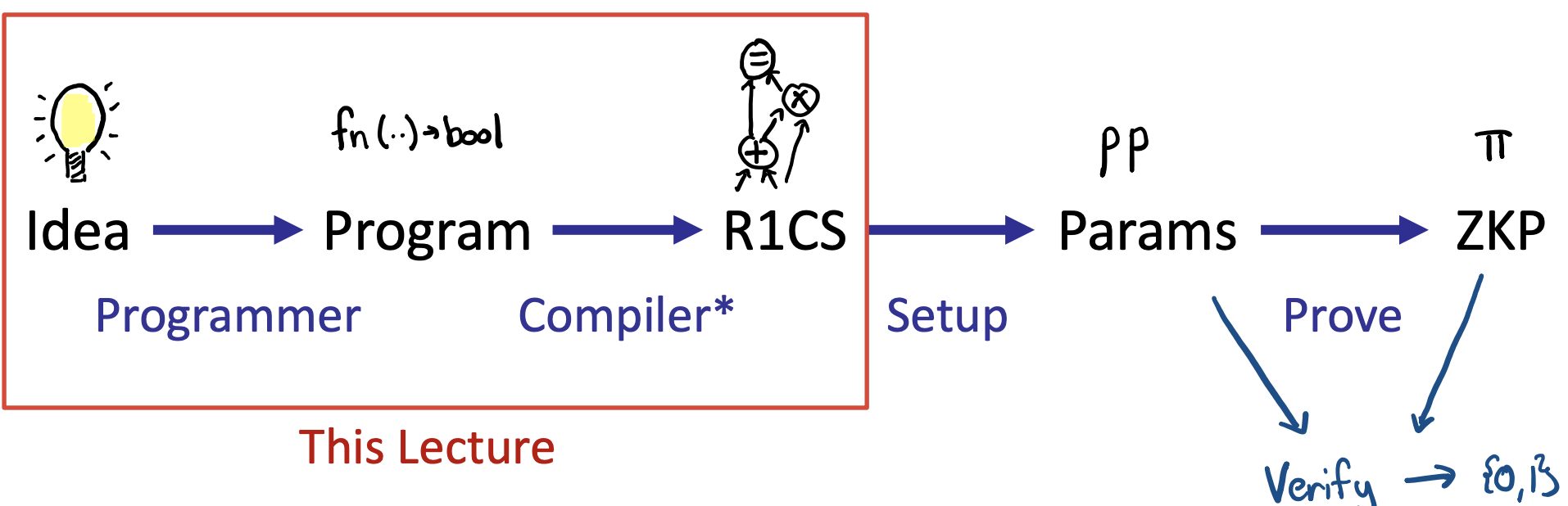
3.1 Big Picture: ZKP programmability
- ZKPs for a predicate $\phi$
- In practice, $\phi$ is an “arithmetic circuit” over inputs x,w
- Arithmetic Circuits (ACs)
- Directed, acyclic graph (DAG)
- Nodes: inputs, gates, constants
- Edges: wires/connections
- R1CS: a common Arithmetic Circuit format
- Definition
- $\phi$ n equations of form
- $alpha \times \beta \eq \gamma$
- affine combinations of variables
- Matrix Definition

- Definition
- Zooming out: a Programming Languages problem

3.2 Using an HDL (+ tutorial)
- PLs vs. HDLs
- Programming Languages (PLs)
- Hardware Description Languages (HDLs)

- HDLs: From Digital to Arithmetic

- Circom Tutorial (Sudoku)Terminal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80pragma circom 2.0.0;
template NonEqual(){
signal input in0;
signal input in1;
signal inv;
// check that (in0 - in1) is non-zero
inv <-- 1/ (in0 - in1);
inv*(in0 - in1) === 1;
}
//all element in the array is unique
template Distinct(n) {
signal input in[n];
component nonEqual[n][n];
for(var i = 0; i < n; i++){
for(var j = 0; j < i; j++){
nonEqual[i][j] = NonEqual();
nonEqual[i][j].in0 <== in[i];
nonEqual[i][j].in1 <== in[j];
}
}
}
// Enforce that 0 <= in < 16
template Bits4(){
signal input in;
signal bits[4];
var bitsum = 0;
for (var i = 0; i < 4; i++) {
bits[i] <-- (in >> i) & 1;
bits[i] * (bits[i] - 1) === 0;
bitsum = bitsum + 2 ** i * bits[i];
}
bitsum === in;
}
// Enforce that 1 <= in <= 9
template OneToNine() {
signal input in;
component lowerBound = Bits4();
component upperBound = Bits4();
lowerBound.in <== in - 1;
upperBound.in <== in + 6;
}
template Sudoku(n) {
// solution is a 2D array: indices are (row_i, col_i)
signal input solution[n][n];
// puzzle is the same, but a zero indicates a blank
signal input puzzle[n][n];
component distinct[n];
component inRange[n][n];
// ensure that puzzle and solution agree
for (var row_i = 0; row_i < n; row_i++) {
for (var col_i = 0; col_i < n; col_i++) {
// we could make this a component
puzzle[row_i][col_i] * (puzzle[row_i][col_i] - solution[row_i][col_i]) === 0;
}
}
for (var row_i = 0; row_i < n; row_i++) {
for (var col_i = 0; col_i < n; col_i++) {
// ensure that each row is distinct
if (row_i == 0) {
distinct[col_i] = Distinct(n);
}
// ensure that each solution # is in range
inRange[row_i][col_i] = OneToNine();
inRange[row_i][col_i].in <== solution[row_i][col_i];
distinct[col_i].in[row_i] <== solution[row_i][col_i];
}
}
}
component main {public[puzzle]} = Sudoku(9);1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27$ make verify
snarkjs powersoftau new bn128 12 tmp.ptau
[INFO] snarkJS: First Contribution Hash:
9e63a5f6 2b96538d aaed2372 481920d1
a40b9195 9ea38ef9 f5f6a303 3b886516
0710d067 c09d0961 5f928ea5 17bcdf49
ad75abd2 c8340b40 0e3b18e9 68b4ffef
snarkjs powersoftau prepare phase2 tmp.ptau sudoku.ptau
rm tmp.ptau
snarkjs groth16 setup sudoku.r1cs sudoku.ptau sudoku.pk
[INFO] snarkJS: Reading r1cs
[INFO] snarkJS: Reading tauG1
[INFO] snarkJS: Reading tauG2
[INFO] snarkJS: Reading alphatauG1
[INFO] snarkJS: Reading betatauG1
[INFO] snarkJS: Circuit hash:
30e22e95 d0529c79 cbce3755 13e3cfca
d1f2e008 45175417 f680792a d284d44b
465f98ae eae388e9 2a4851c2 fdd3e337
bf7dcec7 e22334b6 537f5812 0bc9eb04
snarkjs zkey export verificationkey sudoku.pk sudoku.vk
[INFO] snarkJS: EXPORT VERIFICATION KEY STARTED
[INFO] snarkJS: > Detected protocol: groth16
[INFO] snarkJS: EXPORT VERIFICATION KEY FINISHED
snarkjs groth16 prove sudoku.pk sudoku.wtns sudoku.pf.json sudoku.inst.json
snarkjs groth16 verify sudoku.vk sudoku.inst.json sudoku.pf.json
[INFO] snarkJS: OK!