ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 4: SNARKs via Interactive Proofs (Justin Thaler)
4.1 Interactive Proofs: Motivation and Model
- Interactive Proofs
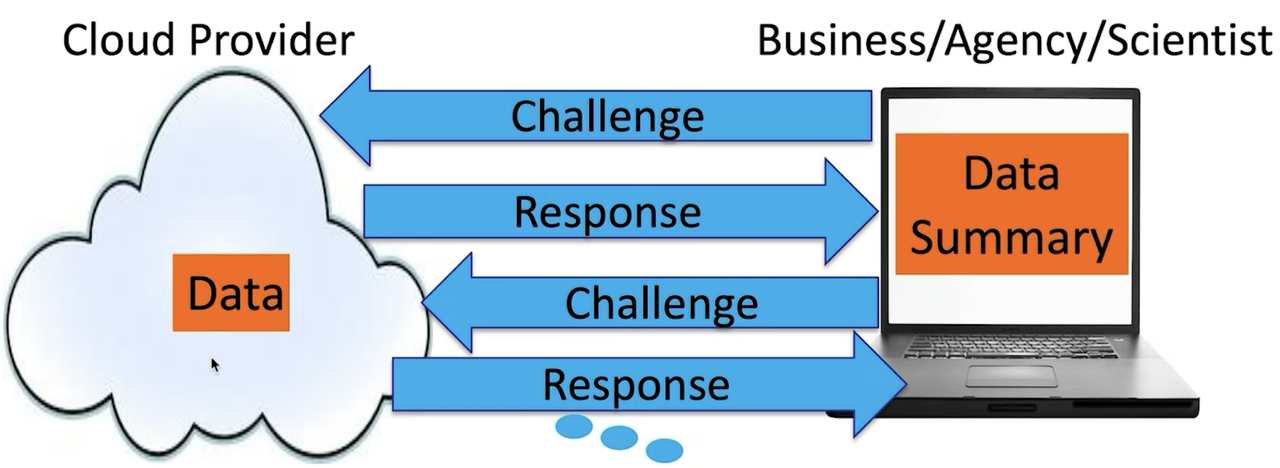
- P solves problem, tells V the answer.
- Then they have a conversation.
- P’s goal: convince V the answer is correct.
- Requirements:
- Completeness: an honest P can convince V to accept.
- (Statistical) Soundness: V will catch a lying P with high probability.
- If soundness holds only against polynomial-time provers, then the protocol is called an interactive argument.
- P solves problem, tells V the answer.
- Interactive Proofs and Arguments
- Compare soundness to knowledge soundness for circuit-satisfiability
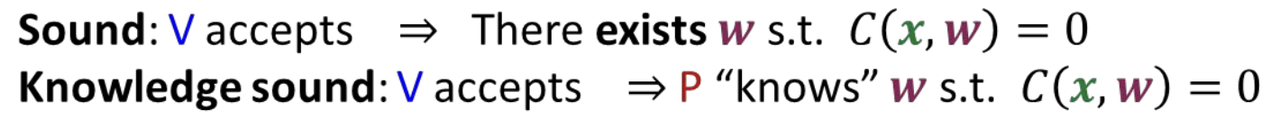
- Knowledge soundness is stronger.
- Compare soundness to knowledge soundness for circuit-satisfiability
- Public Verifiability
- Interactive proofs and arguments only convince the party that is choosing/sending the random challenges
- This is bad if there are many verifiers (as in most blockchain applications).
- P would have to convince each verifier separately.
- For public coin protocols, we have a solution: Fiat-Shamir.
- Makes the protocol non-interactive + publicly verifiable.
4.2 SNARKs from interactive proofs
- Actual SNARK
- P commits cryptographically to W.
- Uses an IP to prove that w satisfies the claimed property.
- Reveals just enough information about the committed witness wto allow V to run its checks in the IP.
- Render non-interactive via Fiat-Shamir.
- P commits cryptographically to W.
- Functional Commitments
- Polynomial commitments
- Multilinear commitments
- Vector commitments (e.g., Merkle trees)
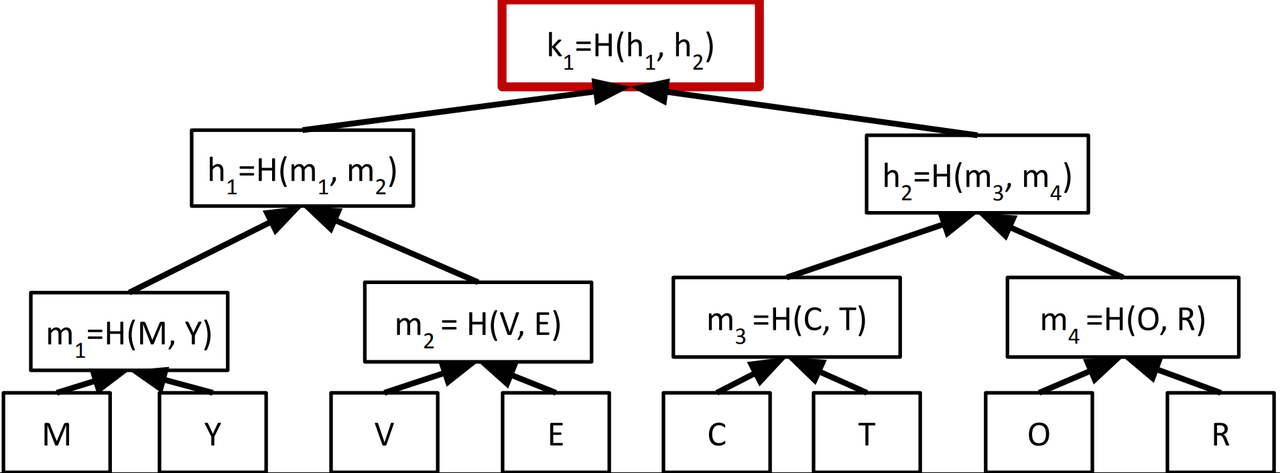
- Merkle trees:
- The commitment
- Opening Leaf T
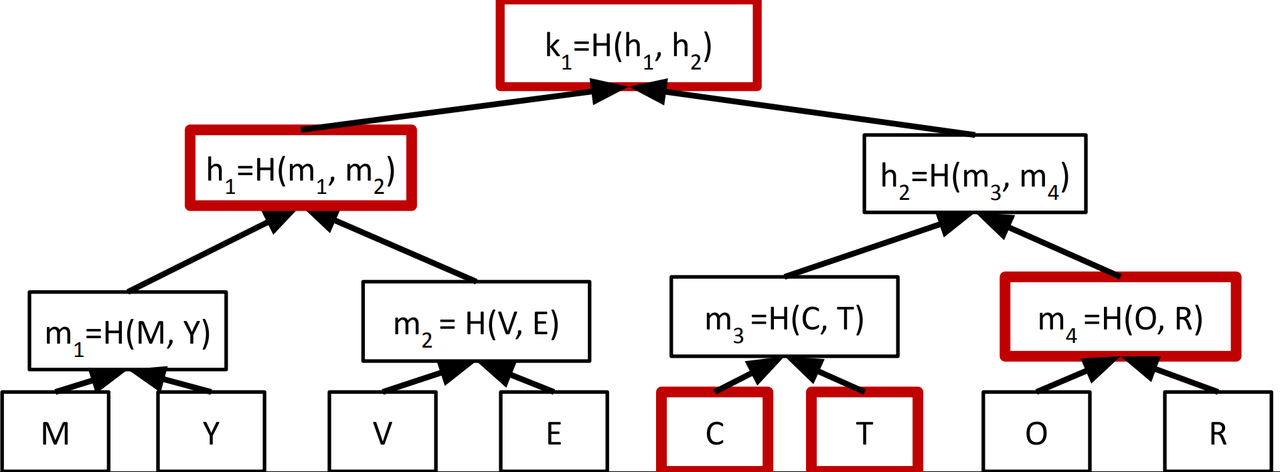
- Provers need to provide T, C, m4, h1, and k1
- “Opening proof” size is O(log n) hash values.
- Provers need to provide T, C, m4, h1, and k1
- (Attampt to) Commit to a univariate f(X) in $F_7[X]$
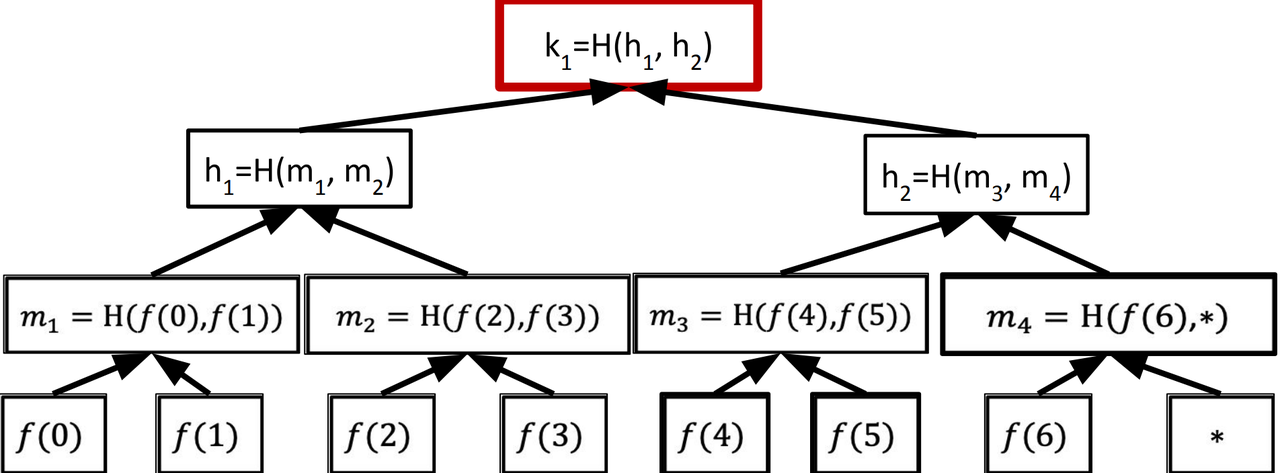
- Reveal f(4)
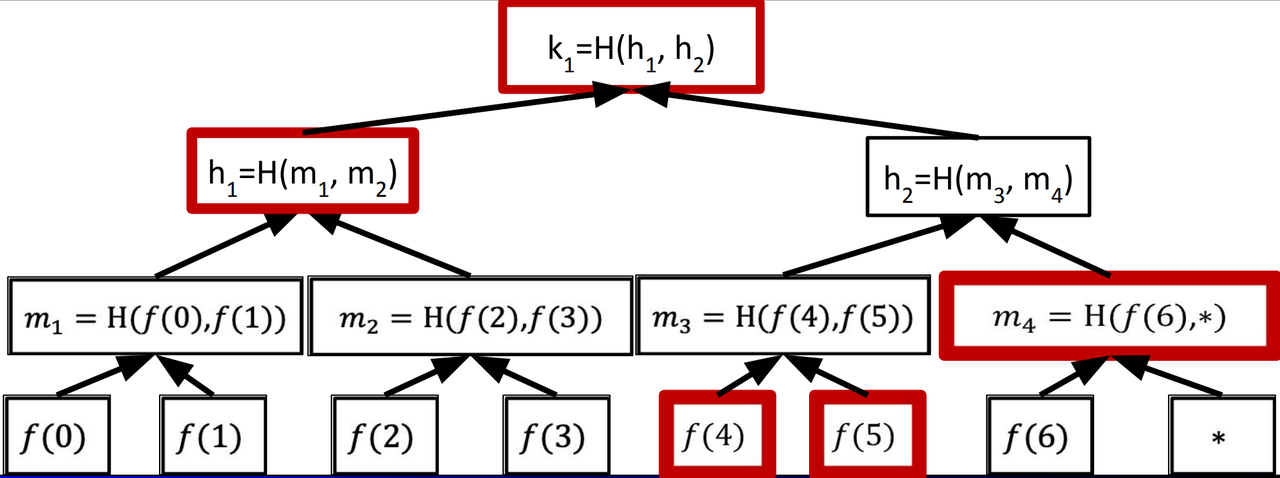
- Problems

- The commitment