ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 4: SNARKs via Interactive Proofs (Justin Thaler)
4.3 Interactive proof design: Technical Preliminaries
- SZDL Lemma
- Equal test (in multivariate polynomials)
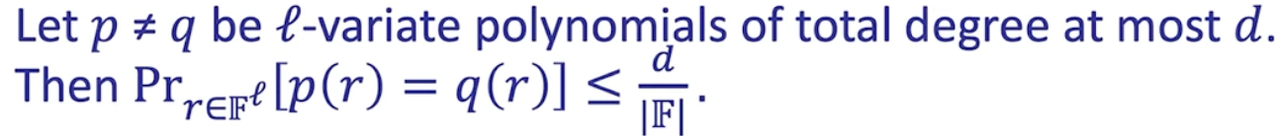
- Equal test (in multivariate polynomials)
- Low-Defree and Multilinear Extensions
- Extensions

- Multilinear Extensions

- Examples
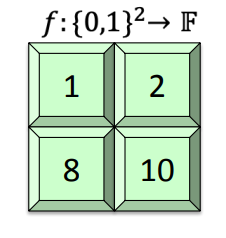
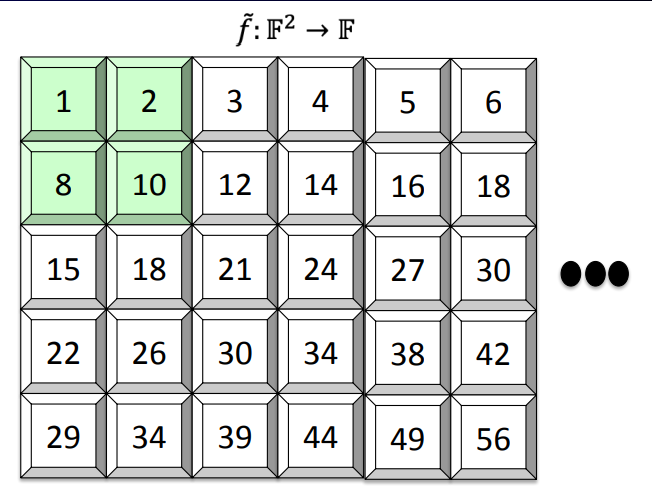
- f(0,0) = 1; f(0,1) = 2; f(1,0) = 8; f(1,1) = 10
- $\tilde{f}(0,0) = 1; \tilde{f}(0,1) = 2; \tilde{f}(1,0) = 8; \tilde{f}(1,1) = 10$
- $\tilde{f}(x_1,x_2) = (1-x_1)(1-x_2)+2(1-x_1)x_2+8x_1(1-x_2)+10x_1x_2$: unique!
- (1-x_1)(1-x_2) term maps inputs (0,0) to 1
- 2(1-x_1)x_2 term maps inputs (0,1) to 2
- …
- Evaluating multilinear extensions quickly
- Use Lagrange Interpolation
- Extensions

- $\tilde{\delta}_w(r)$ maps (0,0) to 1; others to 0
4.4 The Sum-check Protocol [LFKN90]
- Input: V given oracle access to a l-variate polynomial g over filed F.
- Prover负责计算,并把计算结果和proof给Verifier。
- Verifier验证计算结果的正确性
- Goal: compute the quantity
- $\Sigma_{b_1\in{0,1}} \Sigma_{b_2\in{0,1}} \dots \Sigma_{b_l\in{0,1}} g(b_1,\dots,b_l)$
- 最简单的方法,verifier问prover每个点的值然后加起来,需要$2^l$次
- Sum-check Protocol
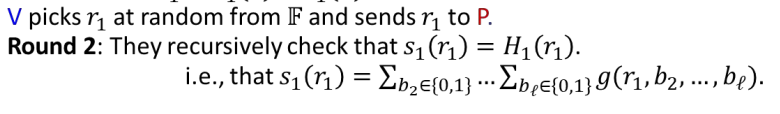
- s1 is the prover actually sent and H1 is what the prover would send if the prover is honest
- H1 is equal to the true answer except it have been cut off the first sum
- H1 is a univariate polynomial

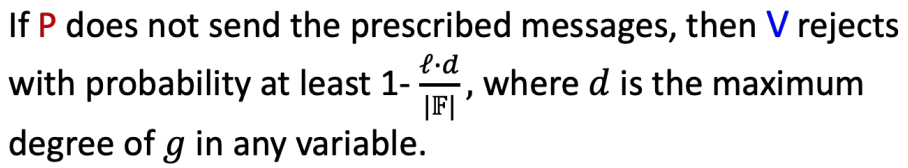
- s1 is the prover actually sent and H1 is what the prover would send if the prover is honest
- Analysis of the sum-check protocol
- Completeness
- Soundness

- Costs of the sum-check protocol
- Application: Counting Triangles
- Input $A \in {0,1}^{n \times n}$, representing the adjacency matrix of a graph
- Output: $\Sigma_{i,j,k\in[n]^3} A_{ij}A_{jk}A_{ik}$
- Time cost in matrix-multiplication: $n^{2.37}$
- The Protocol:
- View A as a function mapping ${0,1}^{\log n} \times {0,1}^{\log n}$ to F
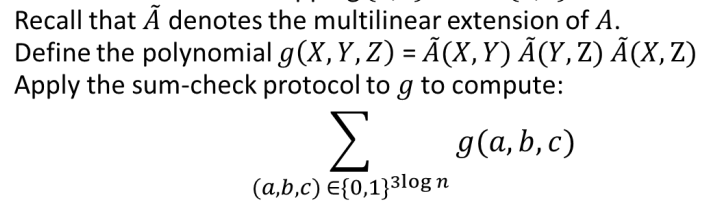
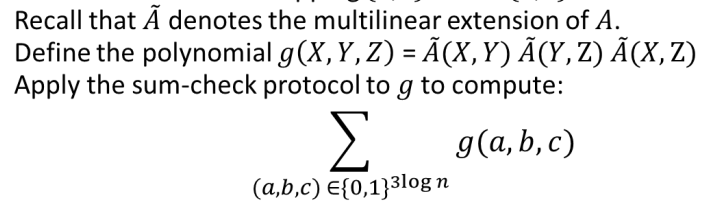
- View A as a function mapping ${0,1}^{\log n} \times {0,1}^{\log n}$ to F
- Cost
- Communication: O(log n)
- V runtime is O(n^2)
- P runtime is O(n^3)
- A SNARK for circuit-satisfiability
- SNARKs for circuit-satisfiability
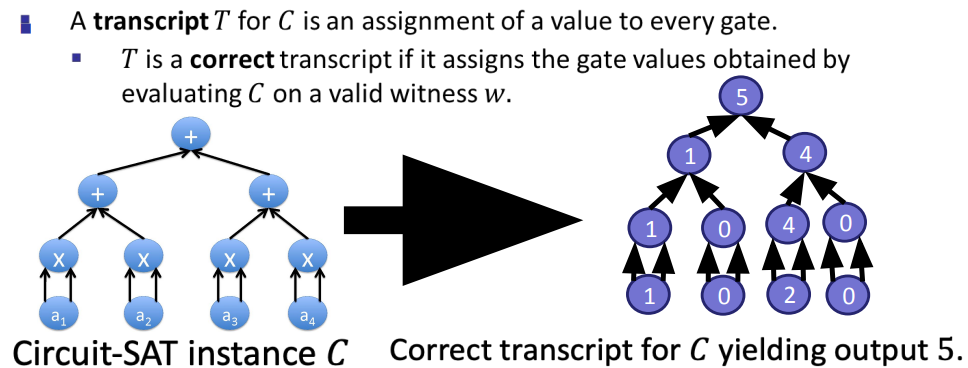
- Viewing a transcript T as a function with domain ${0,1}^{\log S}$
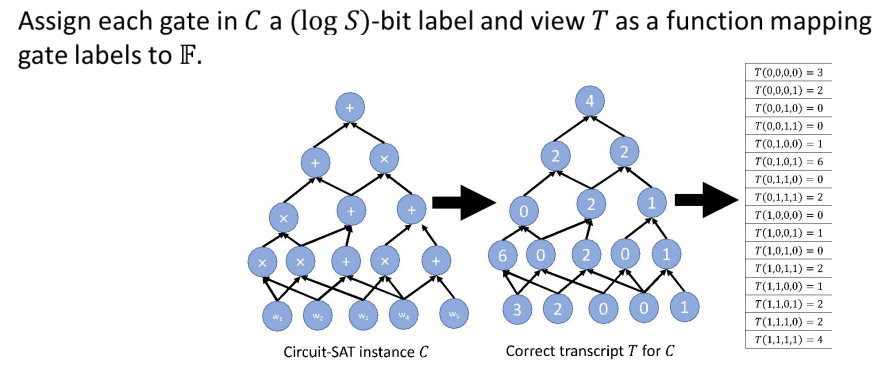
- SNARKs for circuit-satisfiability
4.5 The polynomial IOP underlying the SNARK
- The start of the polynomial IOP

- Intuition for why h is a useful object for P to send
- Think of h as a distance-amplified encoding of the transcript T
- the domain of T is ${0,1}^{\log S}$. The domain of h is $F^{\log S}$
- Even tiny differences in transcripts can get blown up by the extension polynomials into easily detectable differences, in particular that are detectable even by a verifier that is only allowed to evaluate those extension polynomials at a single point.
- Think of h as a distance-amplified encoding of the transcript T
- Intuition for why h is a useful object for P to send
- Two-step plan of attack (这部分没听懂QAQ)




- The polynomial IOP for circuit-satisfiability

