ZKP学习笔记

ZK-Learning MOOC课程笔记

Lecture 5: The Plonk SNARK (Dan Boneh)

5.2 Proving properties of committed polynomials

  • overview
  • Polynomial equality testing with KZG
    • KZG: determined commitment (if the function is equal, then the commitment is equal too)
      • If the $com_f = com_g$, the verifier can tell if $f=g$ on its own???
      • but
        • The verifier does not have the commitment of $g_1g_2g_3$
  • Important proof gadgets for univariates
    • The size k is much smaller than d
  • The vanishing polynomial
    • Outside the $\Omega$, the polynomial could evaluate an arbitrary value
    • Verifiers can evaluate the vanishing polynomial very fast.
  • ZeroTest
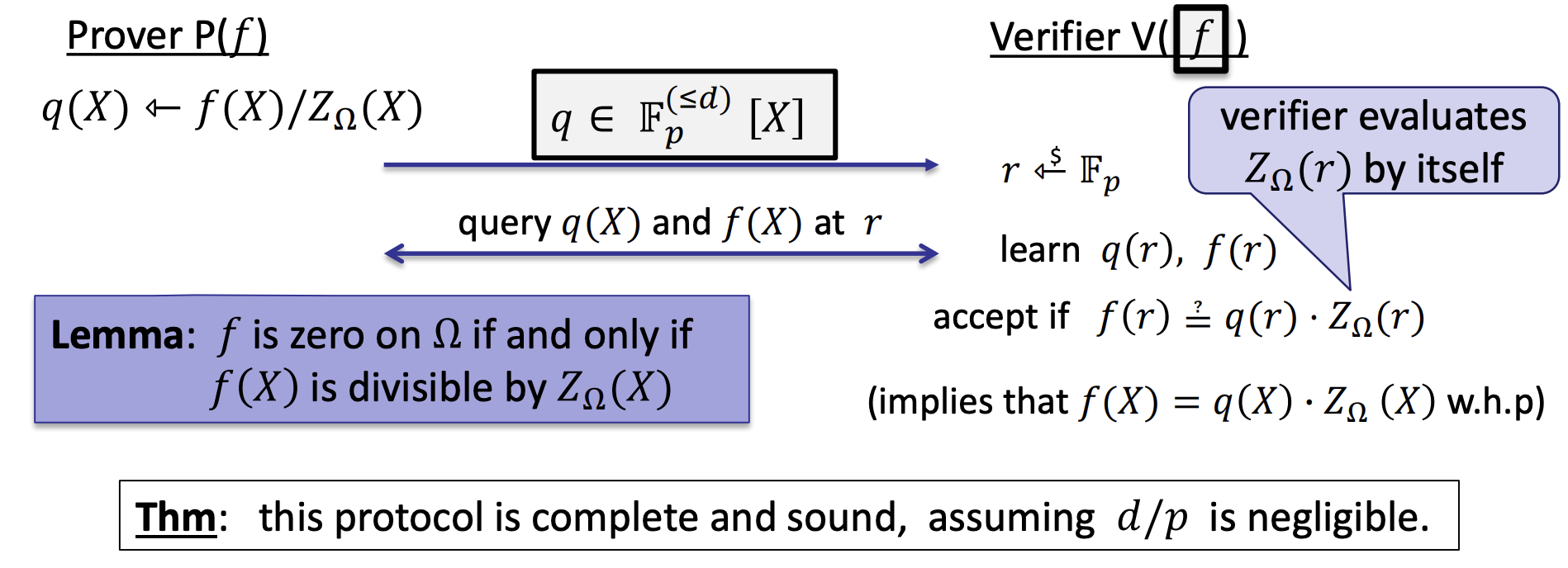
    • F is zero on $\Omega$: All the elements of $\Omega$ are the root of the polynomial.
    • Verifier time: O(log k) and two poly queries (but can be done in one batch)
    • Prover time: dominated by the time to compute q(X) and then commit to q(X)
  • Product check
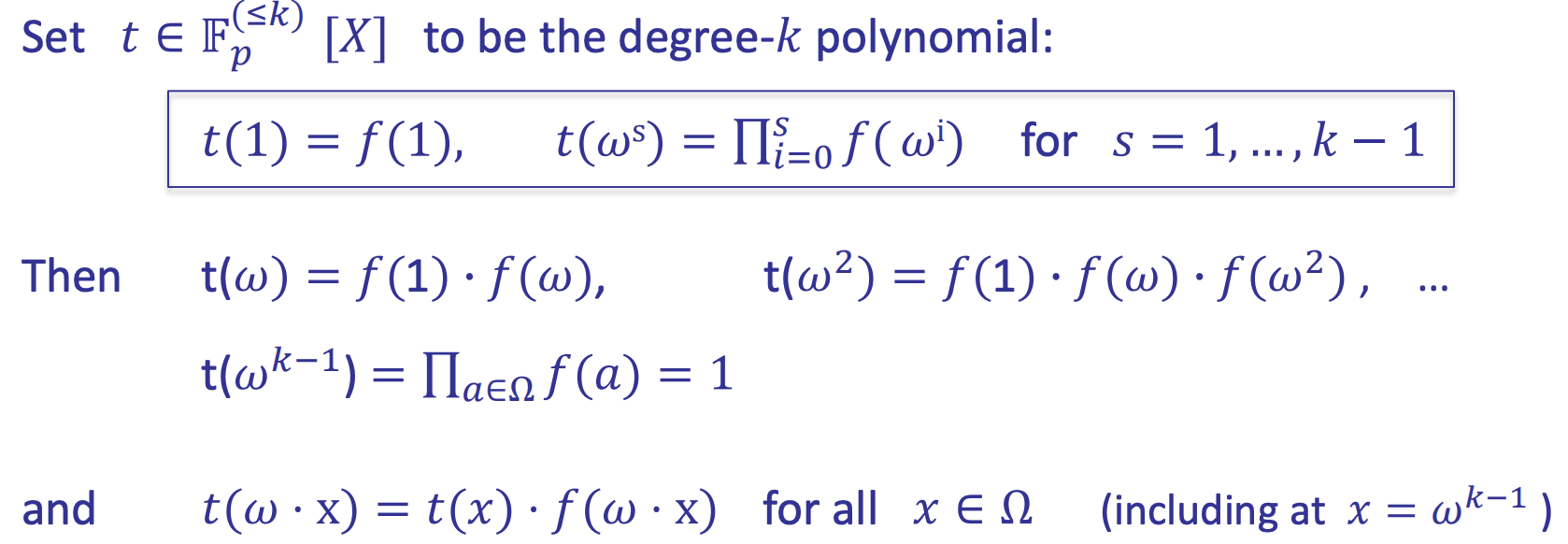
    • Polynomial t: auxiliary polynomial

      • Use the ZeroTest
      • Proof size: two commits, five evals (can be batched).
      • Verifier time: O(logk)
      • Prover time:O(klogk)
    • For rational functions
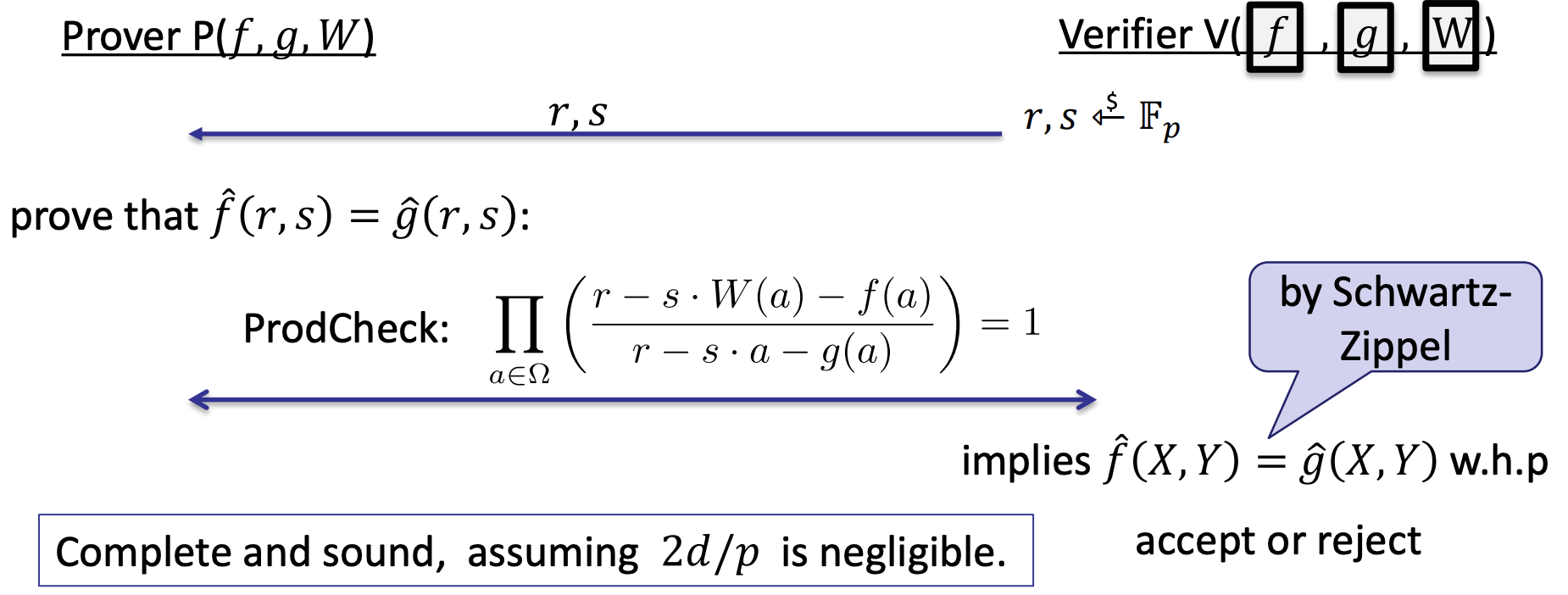
  • Permutation check

    • $\hat{f}$ and $\hat{g}$ is identical
  • Embellished permutation check
    • The two vectors are permutations to each other
    • They also satisfy a prediscribed pumutation




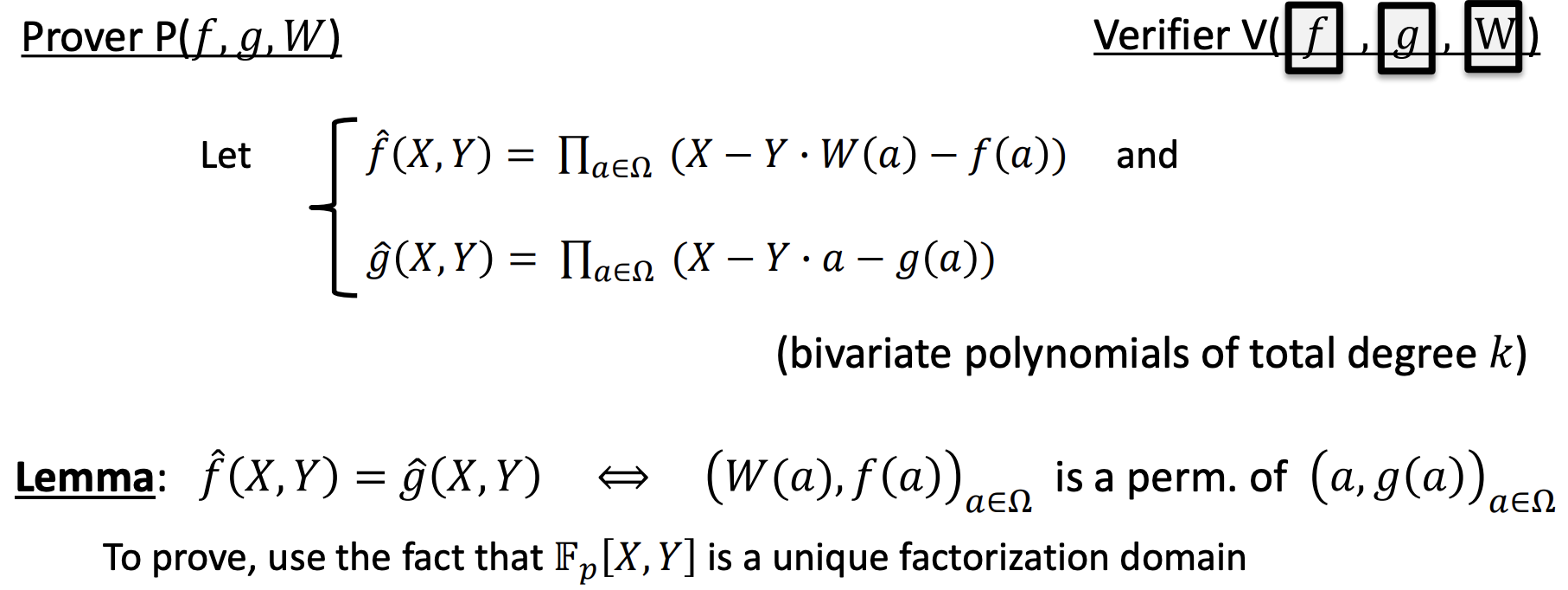
  • Summary of proof gadgets

5.3 The PLONK IOP for general circuits

  • PLONK widely used in practice
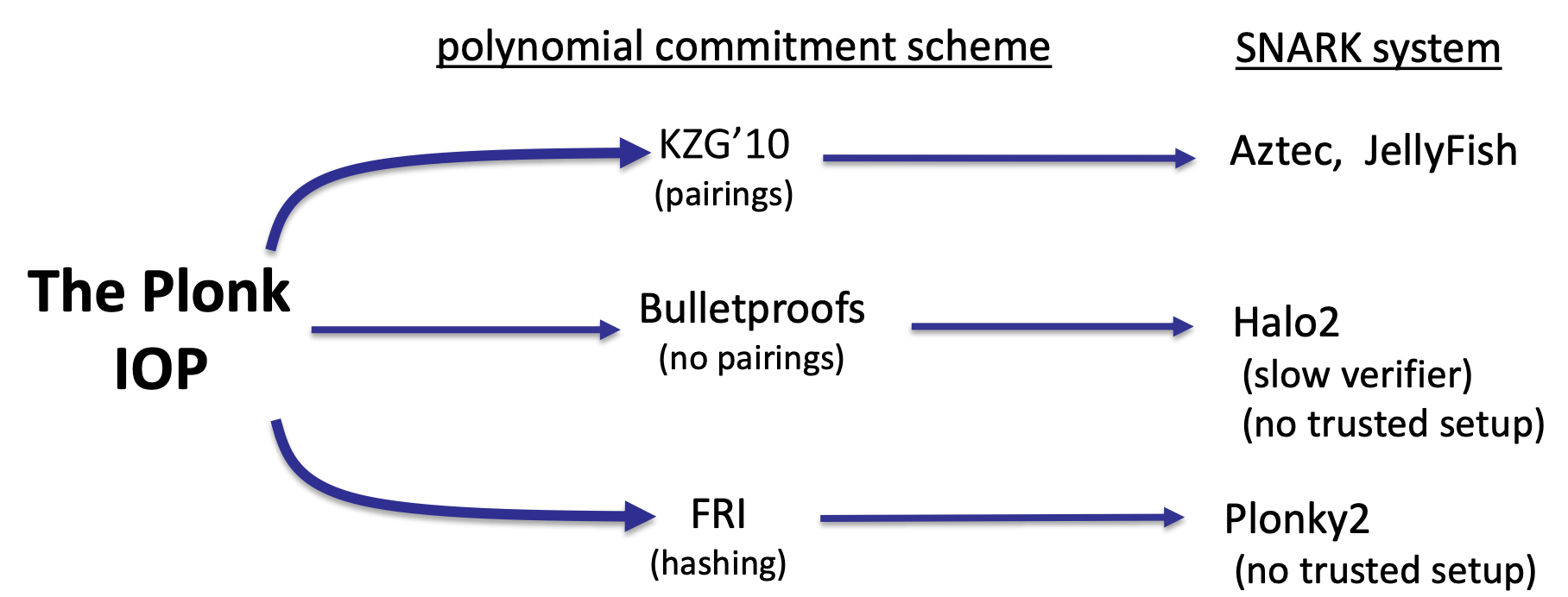
  • PLONK: a poly-IOP for a general circuit
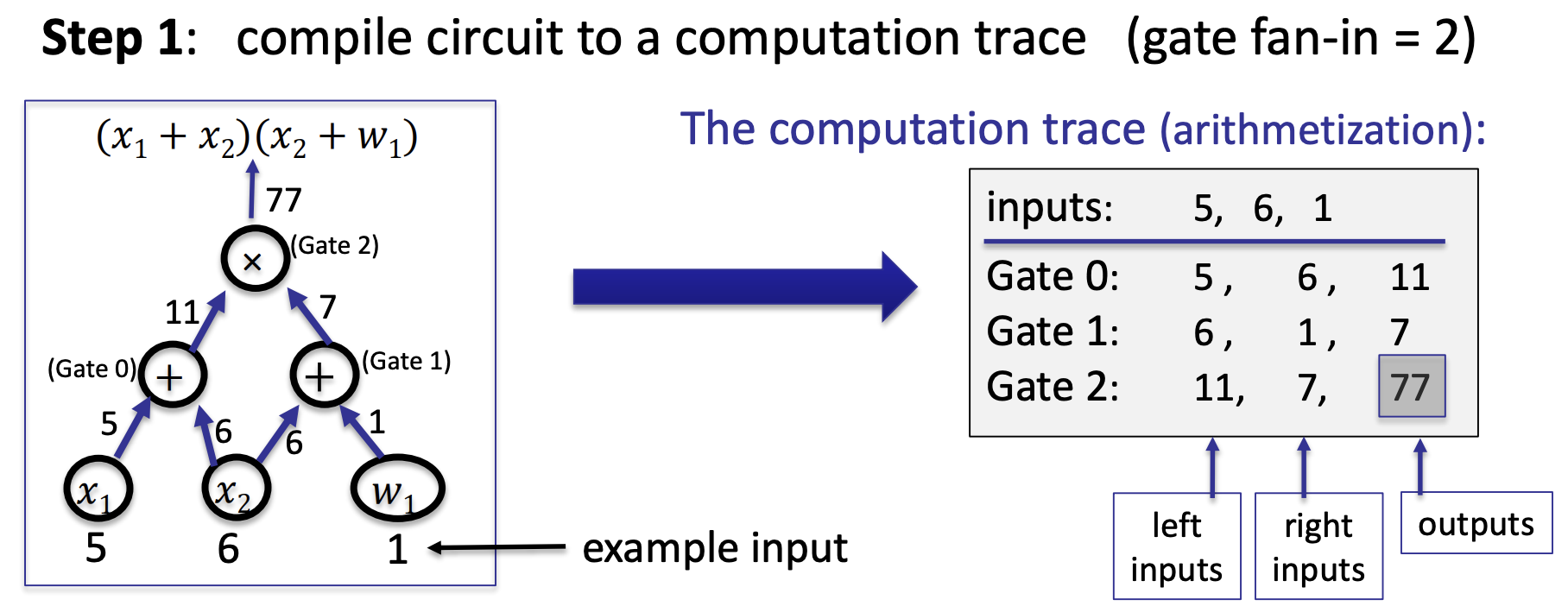
    • Encoding the trace as a polynomial


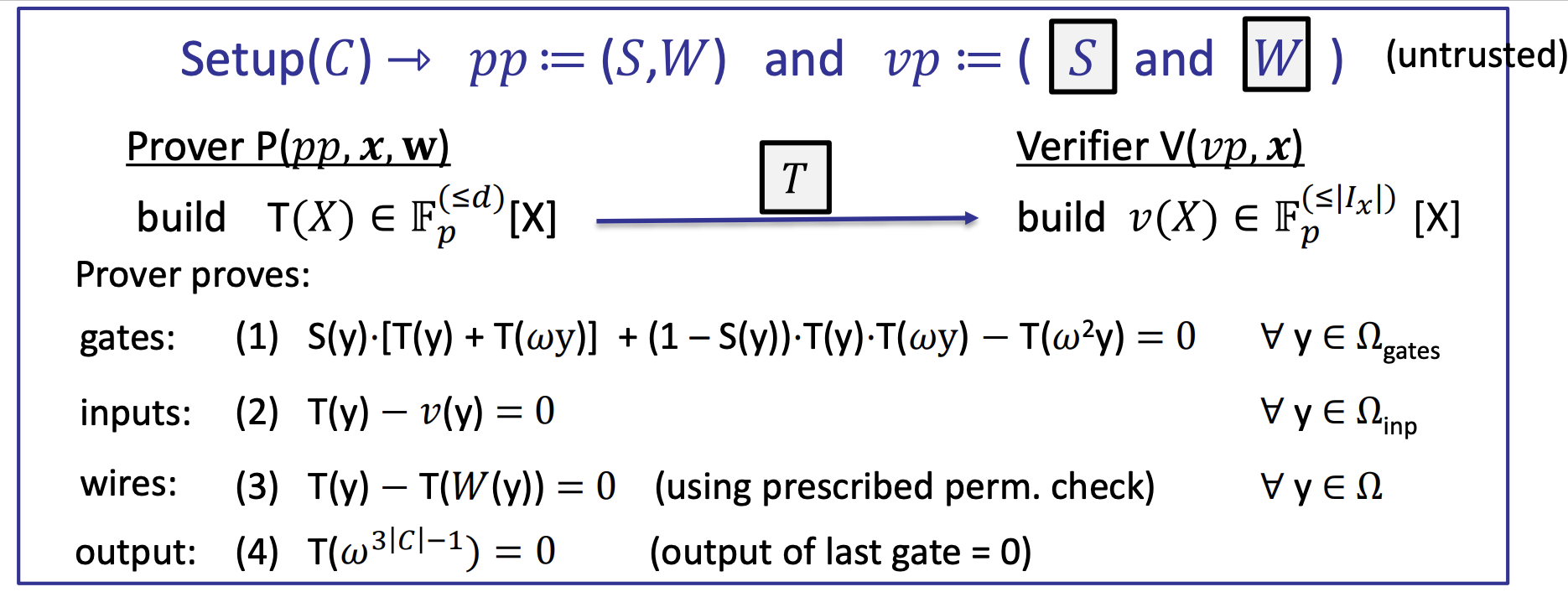
    • Step 2: proving validity of T
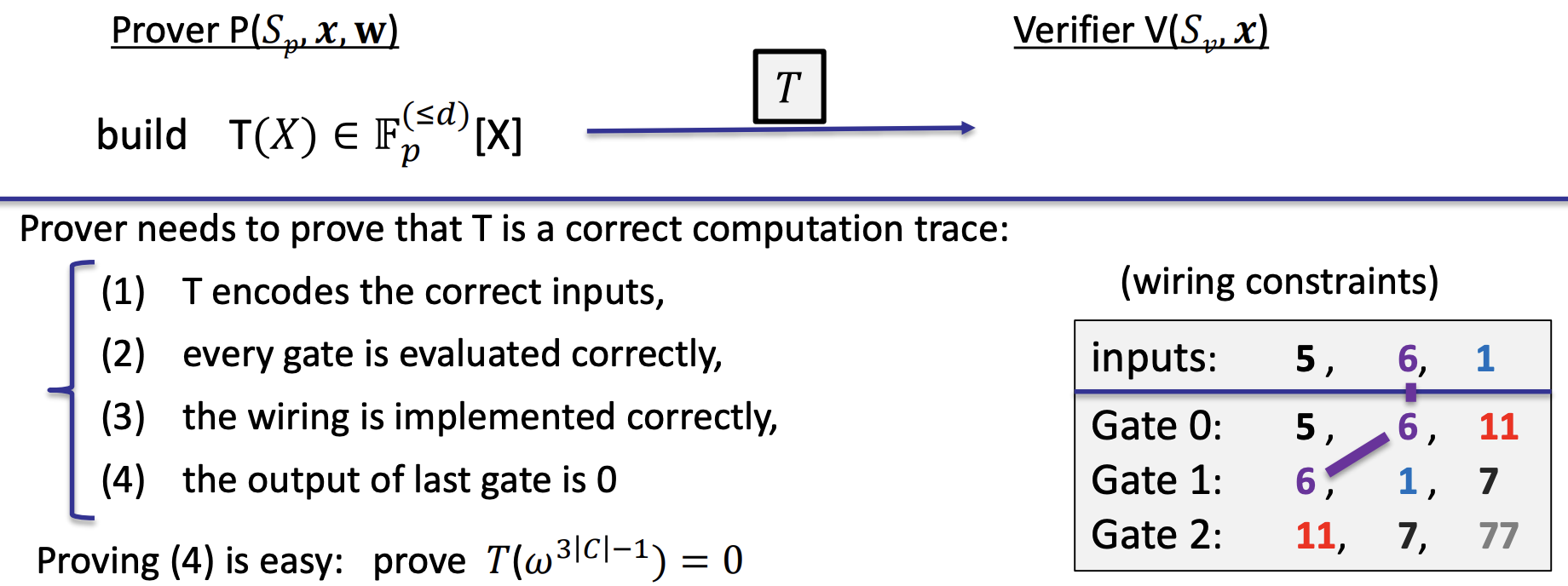
      • (4): the output of the last gate is what the verifier is expecting
      • Proving (1): T encodes the correct inputs

      • Proving (2): every gate is evaluated correctly
        • S(X) is a selector
        • Pre-processing: create the commitment of S(X), it is independent to any input.



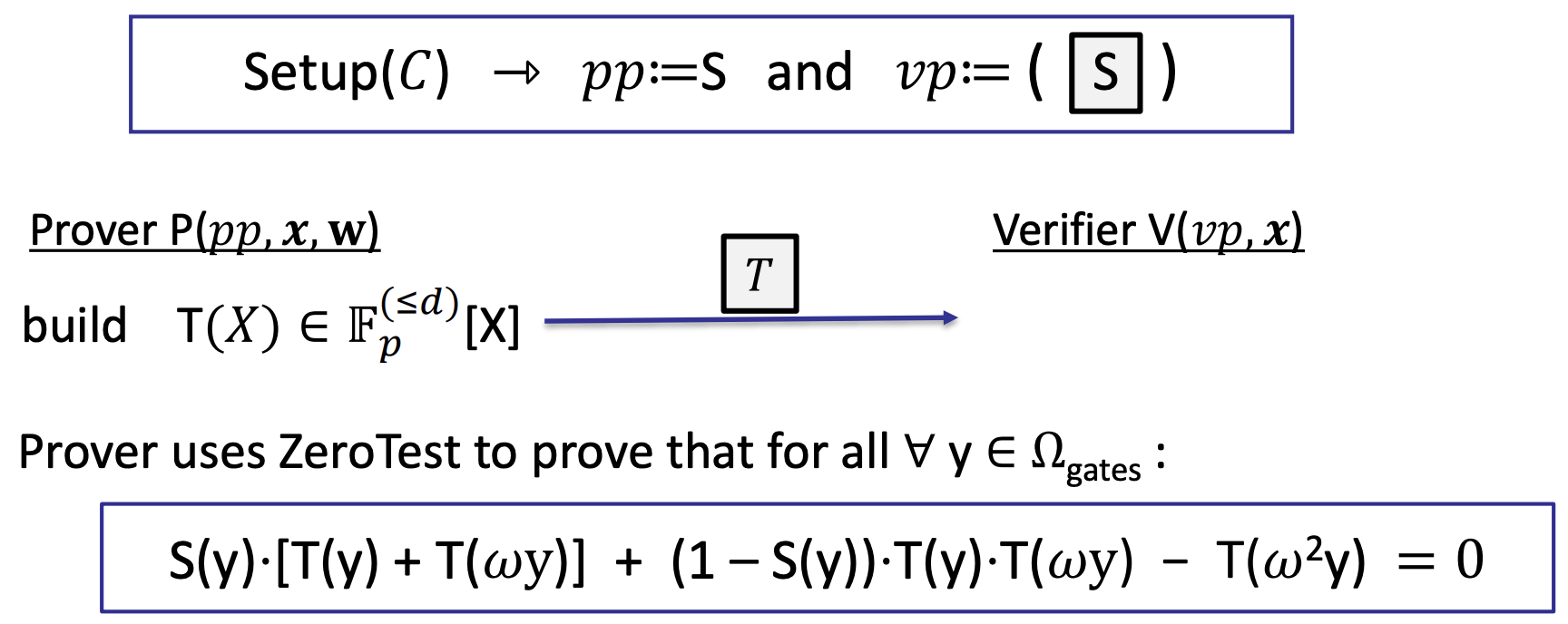
- Proving (3): the wiring is correct

- The W is independent of the inputs
- Prescribed pumutation check

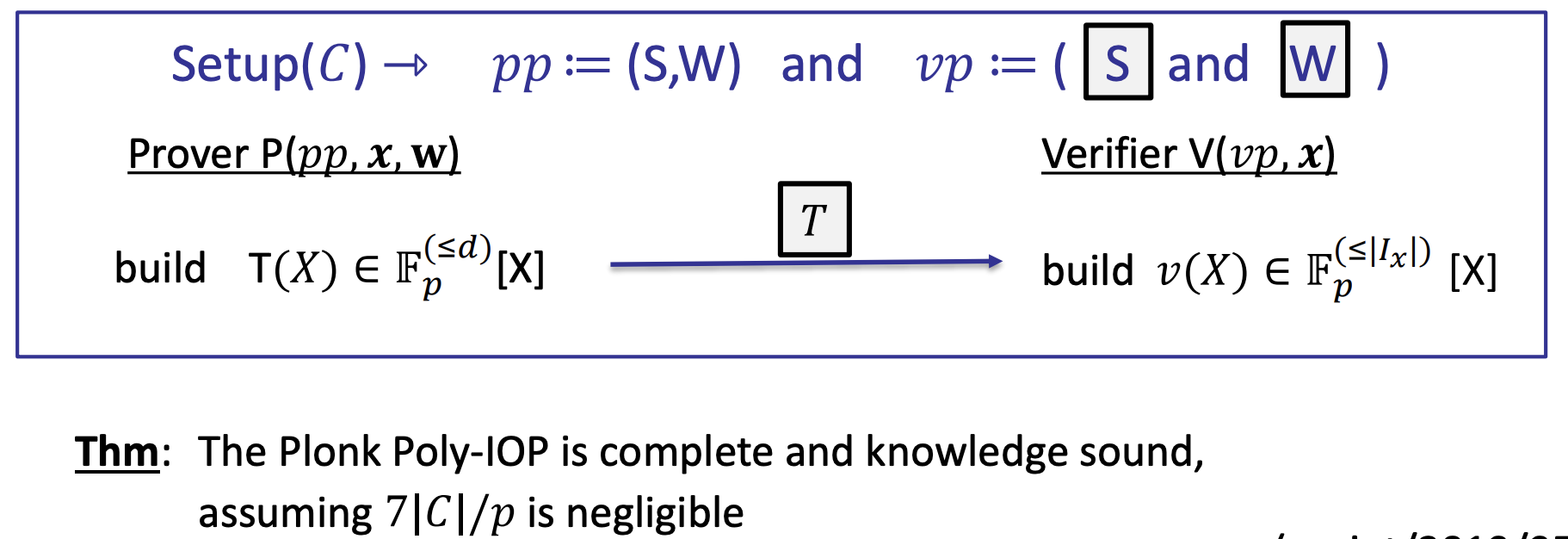
  • The complete Plonk Poly-IOP (and SNARK)

  • Many extensions
    • The SNARK can easily be made into a zk-SNARK
    • Main challenge: reduce prover time
    • A generalization: plonkish arithmetization
      • Plonk for circuits with gates other than + and × on rows (custom gates)
      • More columns on the table