ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang)
- Recall
- How to build an efficient SNARK?
- A polynomial commitment scheme + A polynomial interactive oracle proof (IOP) = SNARK for general circuits
- Plonk
- Univariate polynomial commitment + Plonk Polynomial IOP = SNARK for general circuits
- Interactive proofs
- Multivariate polynomial commitment + Sumcheck protocol = SNARK for general circuits
- polynomial commitment
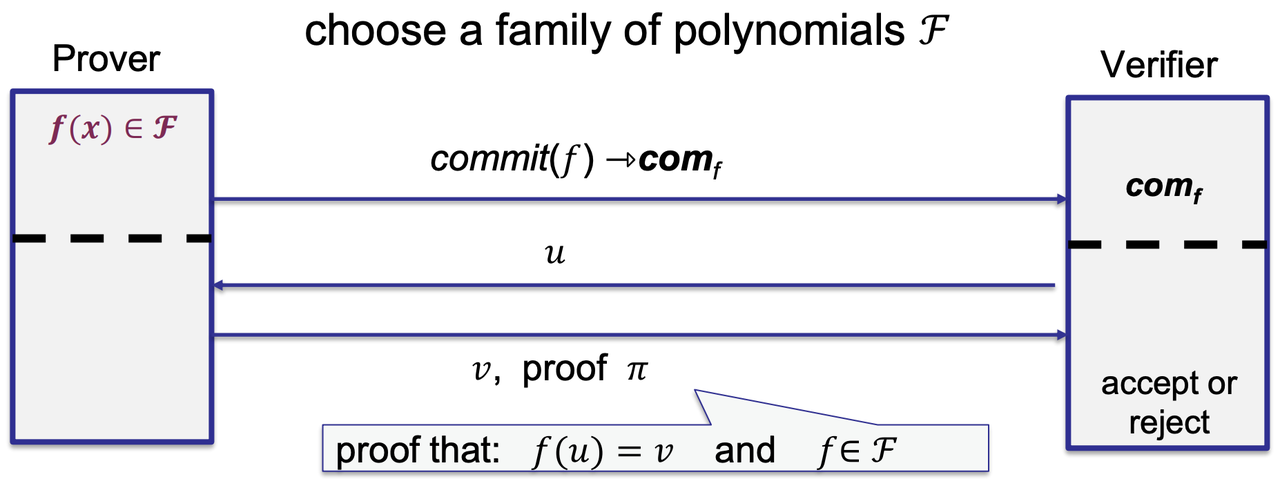

- How to build an efficient SNARK?
6.1 Background
- Group: Closure, Associativity, Identity, Inverse.
- Generator of a group: An element $g$ that generates all elements in the group by taking all powers of $g$
- Discrete logarithm assumption
- A group $G$ has an alternative representation as the powers of the generator $g$: ${g, g^2, g^3,…,g^{p-1}}$
- Discrete logarithm problem: given $y \in G$, find $x$ s.t. $g^x = y$
- Discrete-log assumption: discrete-log problem is computationally hard.
- (Computational) Diffie-Hellman assumption: Given $G, g, g^x, g^y$, cannot compute $g^{xy}$
- Bilinear pairing:
- $(p, G, g, G_T, e)$
- $G$ and $G_T$ are both multiplicative cyclic groups of order $p$, $g$ is the generator of $G$.
- $G$: base group, $G_T$ target group
- Pairing: $e(P^x,Q^y) = e(P,Q)^{xy}$
- Example: $e(g^x,g^y) = e(g,g)^{xy} = e(g^{xy},g)$
- Given $g^x$ and $g^y$ , a pairing can check that some element $h = g^{xy}$ without knowing $x$ and $y$.
- BLS signature [Boneh–Lynn–Shacham’2001]
