ZKP学习笔记

ZK-Learning MOOC课程笔记

Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang)

6.2 KZG polynomial commitment and its variants

  • KZG: [Kate-Zaverucha-Goldberg ‘2010]
  • Procedure



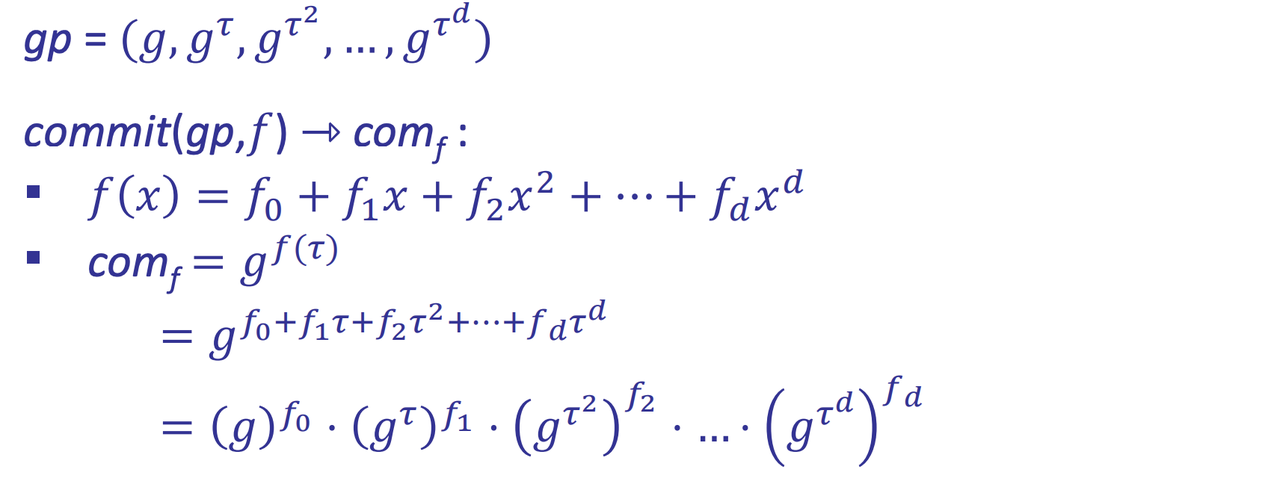
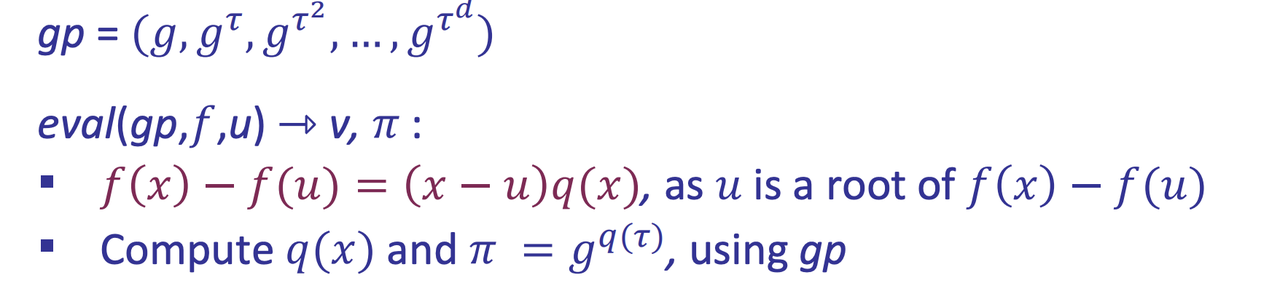
    • Soundness: q-Strong Bilinear Diffie-Hellman (q-SBDH) assumption
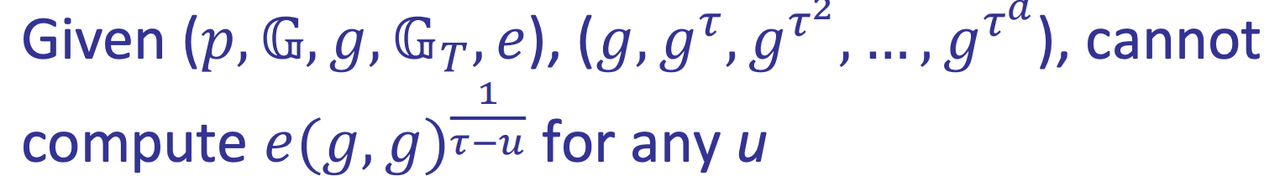
      • Formal Security Proof
        • The key idea: decompose the fack value $v*$ into a correct value $f(u)$ and a difference $\delta$
    • Knowledge soundness and KoE assumption
      • KZG with knowledge soundness: the commitment size is doubled
      • Solution: Generic group model (GGM) [Shoup’97, Maurer’05]
        • GGM can replace the KoE assumption and reduce the commitment size in KZG.
    • Properties of the KZG poly-commit
    • Ceremony: A distributed generation of gp s.t. No one can reconstruct the trapdoor if at least one of the participants is honest and discards their secrets
  • Variants of KZG polynomial commitment
    • Multivariate poly-commit [Papamanthou-Shi-Tamassia’13]
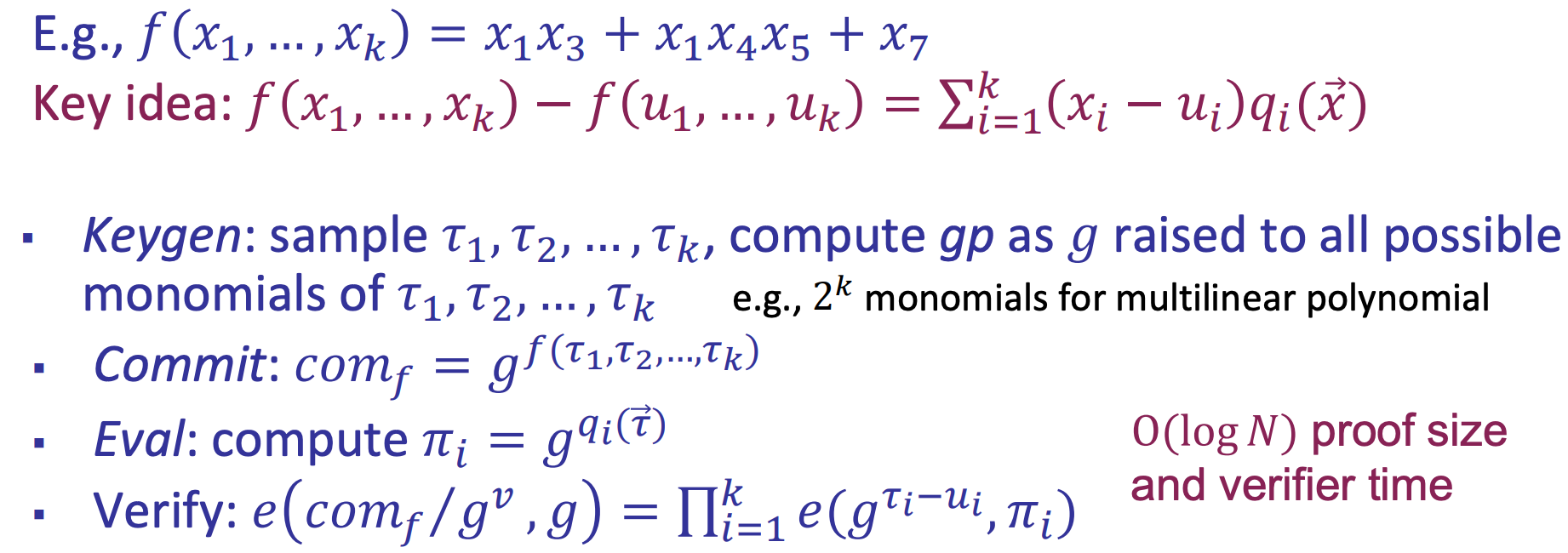
    • Achieving zero-knowledge [ZGKPP’2018]
    • Batch opening
      • single polynomial
      • multiple polynomials
  • Application
    • Plonk [Gabizon-Williamson-Ciobotaru’20]
      • Univariate KZG + Plonk Polynomial IOP
    • vSQL[ZGKPP’17], Libra[XZZPS’19]
      • Multivariate KZG + Sumcheck protocol / GKR protocol