ZKP学习笔记

Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang)

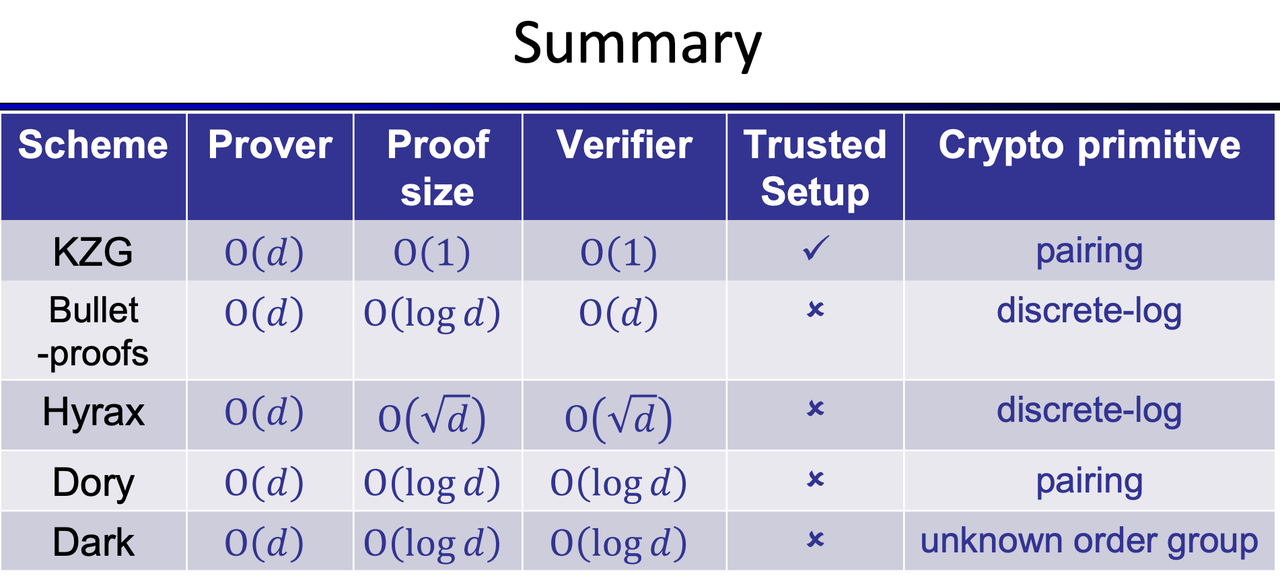
KZG:
- Pros:
  - Commitment and proof size: O(1), 1 group element
  - Verifier time: O(1) pairing
- Cons: trusted setup
Bulletproofs [BCCGP’16, BBBPWM’18]
Transparent setup: sample random $g_0, g_1, g_2, …, g_d$ in $G$
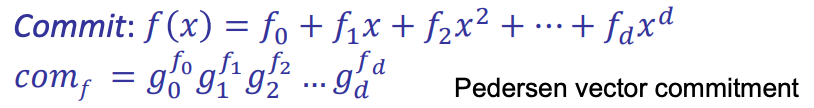
High-level idea
- Example: 3-degree polynomial
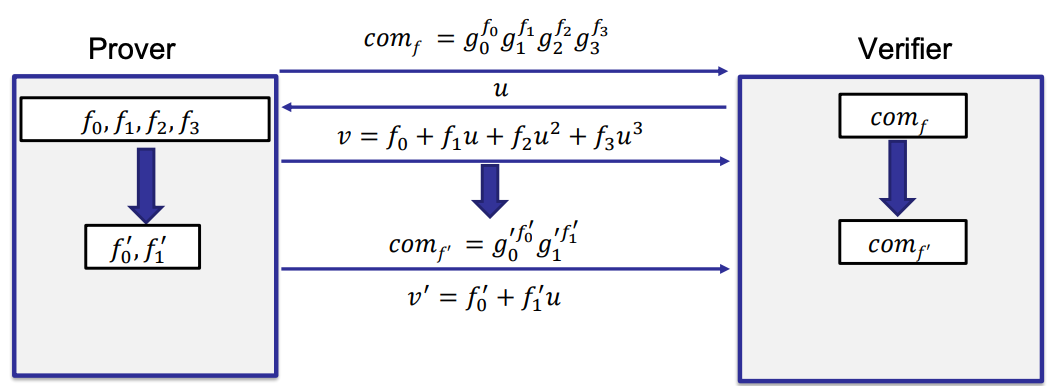
- Degree reduction: 3 degree -> 1 degree -> constant degree
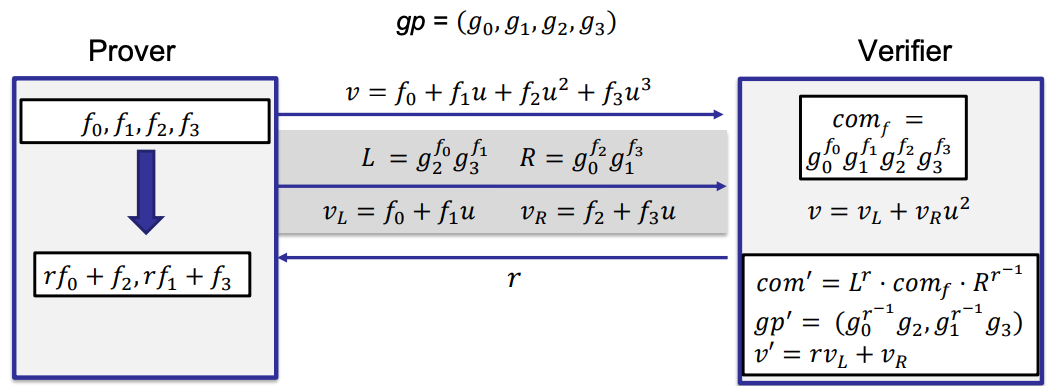
- Cross term to commit L and R
- Similar with FFT
Correctness
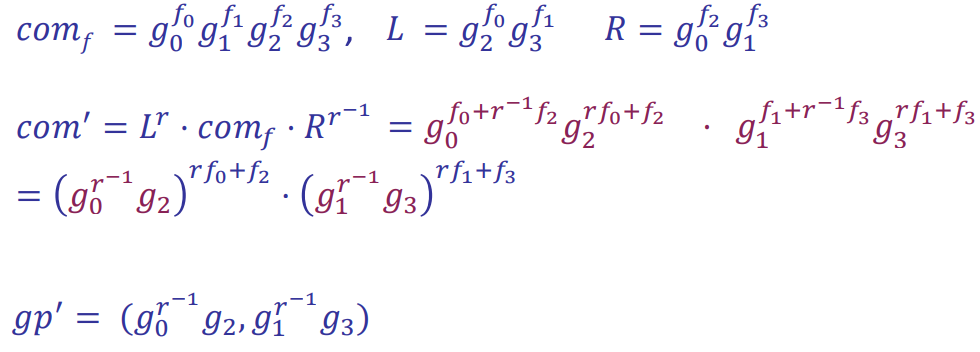
Eval and Verify
Properties of Bulletproofs
- Keygen: O(d), transparent setup!
- Commit: O(d) group exponentiations, O(1) commitment size
- Eval: O(d) group exponentiations (non-interactive via Fiat Shamir)
- Proof size: O(log d)
- Verifier time: O(d)
Other improvement
- Hyrax [Wahby-Tzialla-shelat-Thaler-Walfish’18]
  - Improves the verifier time to O(d) by representing the coefficients as a 2-D matrix
  - Proof size: O($\sqrt{d}$)
- Dory [Lee’2021]
  - Base on pairing
  - Improving verifier time to O(log d)
  - Key idea: delegating the structured verifier computation to the prover using inner pairing product arguments [BMMTV’2021]
  - Also improves the prover time to O($\sqrt{d}$)exponentiations plus O(d) field operations
- Dark [Bünz-Fisch-Szepieniec’20]
  - Based on group of unknown order
  - Achieves O(log d) proof size and verifier time
    - Delegate some part of verifier to the prover
Summary