ZKP学习笔记

ZK-Learning MOOC课程笔记

Lecture 7: Polynomial Commitments Based on Error-correcting Codes (Yupeng Zhang)

7.2 Polyneomial commitment based on error-correcting codes

  • Recall: polynomial commitment
    • Four algorithms
      • Keygen, Commit, Eval, Verify
  • Polynomial coefficients in a matrix
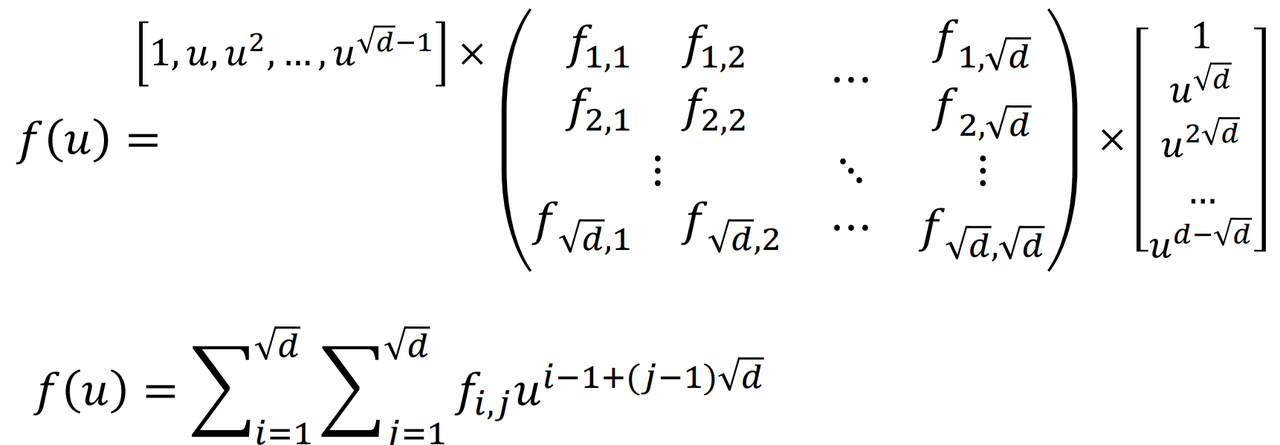
    • The coefficients of the polynomial is a matrix
    • If the number of degrees of the polynomial is not the power of an integer, you can pad it.
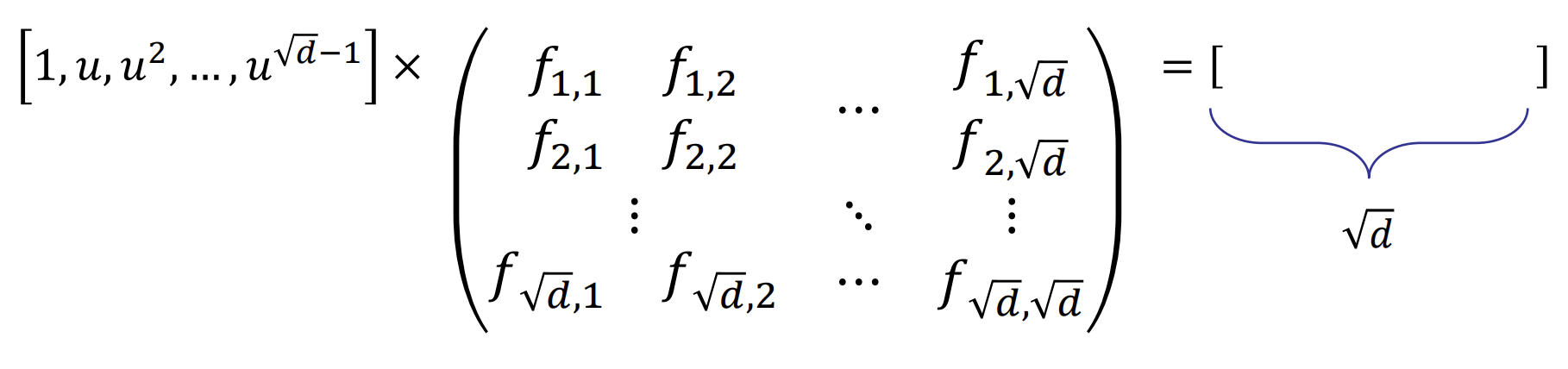
    • Argument for Vec-Mat product
      • Polynomial commitment with $\sqrt{d}$ proof size
  • Encoding the polynomial
    • Design a scheme to test the Vec-Mat product without sending the matrix directly to the verifier
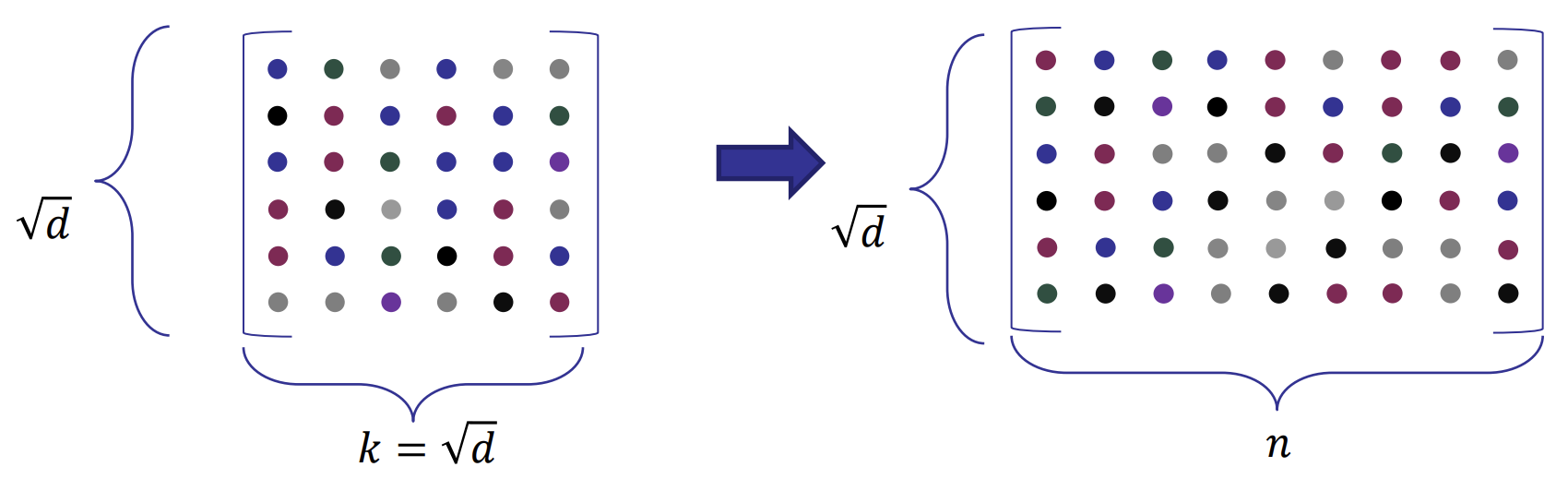
      • Encode each row of the matrix to a linear code
  • Committing the polynomial: Merkle Hash Tree
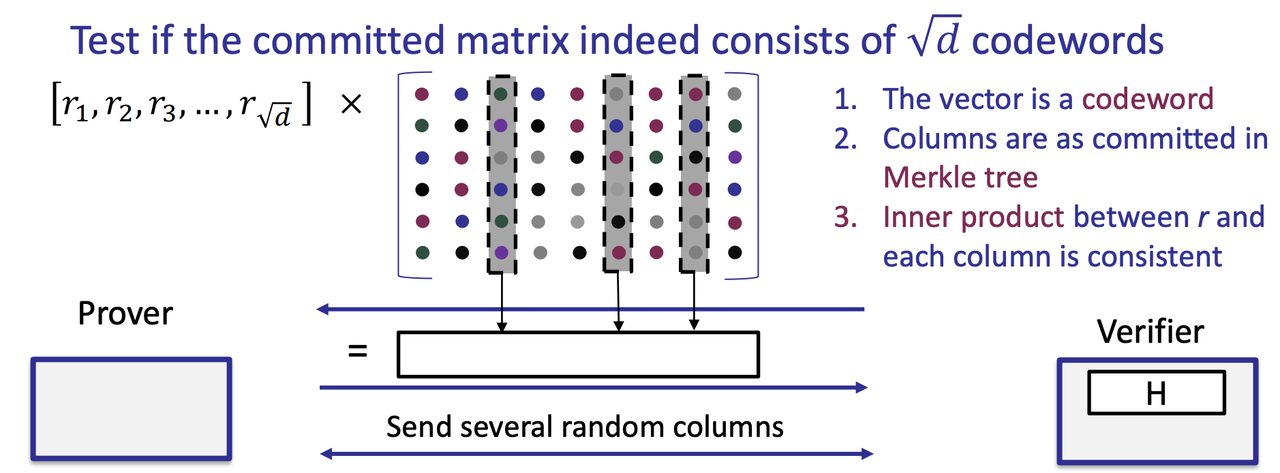
    • Commit to each column of the encoded matrix using Merkle tree (each column is a leaf, verifier can choose a column to ask prover to open)
  • Step 1: Proximity test
    • Ligero [AHIV’2017] and [BCGGHJ’2017]
      • [BCGGHJ’2017] : Ideal linear commitment model. Linear-time encodable code → first SNARK with linear prover time
    • One optimization
      • Prover decodes the proof to a message (size k), and sends k to the verifier
        • Decrease the size of proof from n to k
        • The Verifier does not take the first step of check
  • Step 2: Consistency check
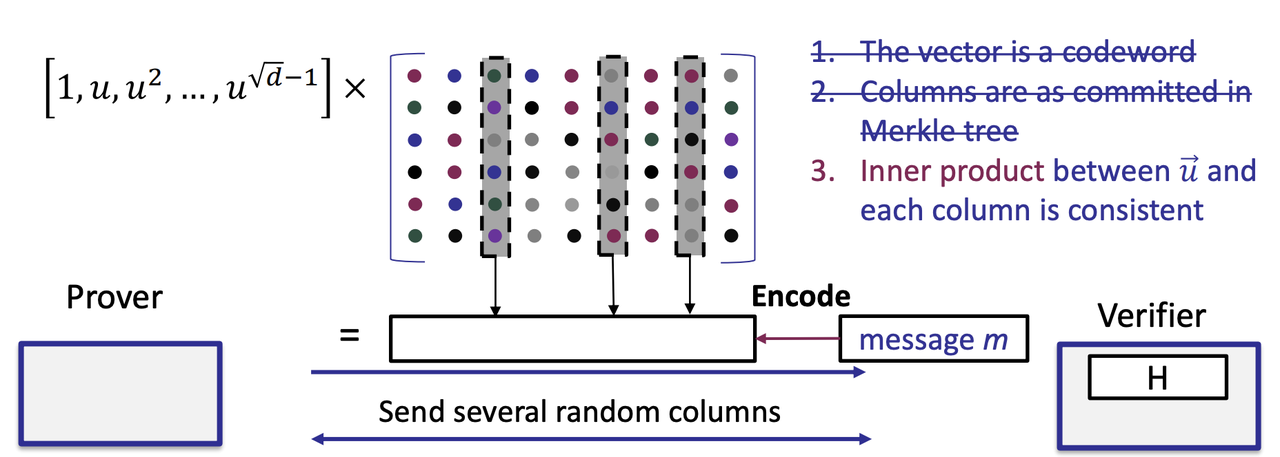
    • The vector u is not random chosen, so the Proximity test is necessary.
  • Summary: Poly-commit based on linear code
    • Keygen: sample a hash function
    • Commit: encode the coefficient matrix of f row-wise with a linear code, compute the Merkle tree commitment
    • Eval and Verify:
      • Proximity test: random linear combination of all rows, check its consistency with t random columns
      • Consistency test: $u \times F = m$, encode m and check its consistency with t random columns
      • f(u) = $m \times u’$
  • Properties of the polynomial commitment
    • Keygen: O(1), transparent setup!
    • Commit:
      • Encoding: O(d logd) field multiplications using RS code, O(d) using linear-time encodable code
      • Merkle tree: O(d) hashes, O(1) commitment size
    • Eval: O(d) field multiplications (non-interactive via Fiat Shamir)
    • Proof size: O($\sqrt{d}$)
    • Verifier time: O($\sqrt{d}$)