ZKP学习笔记
ZK-Learning MOOC课程笔记
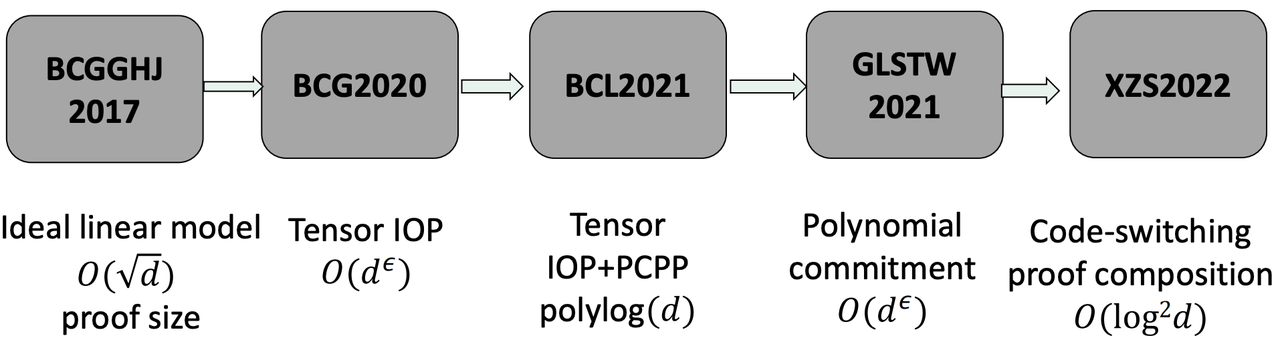
Lecture 7: Polynomial Commitments Based on Error-correcting Codes (Yupeng Zhang)
7.3 Linear-time encodable code based on expanders
- SNARKs with linear prover time
- Linear-time encodable code [Spielman’96][Druk-Ishai’14]
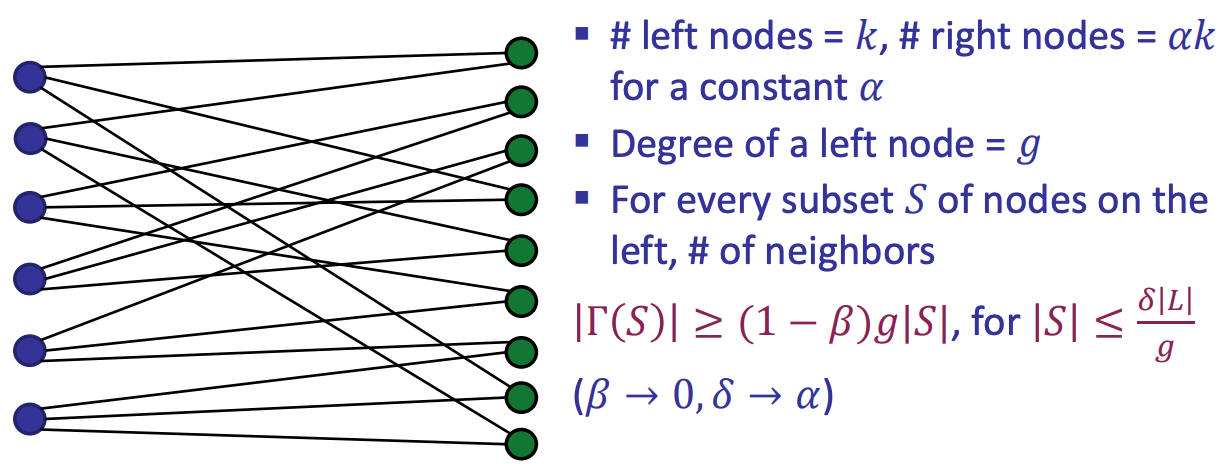
- Bi-parties graph
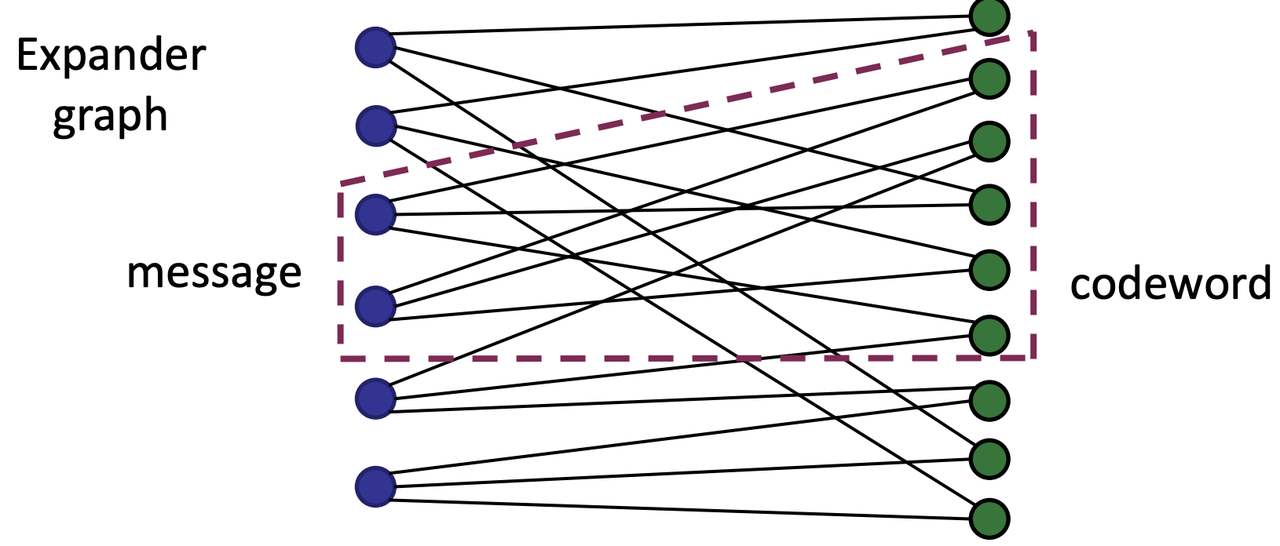
- Left nodes: message
- Right nodes: codeword = sum of the connected node in the left (summation of the values of the its neighbers)
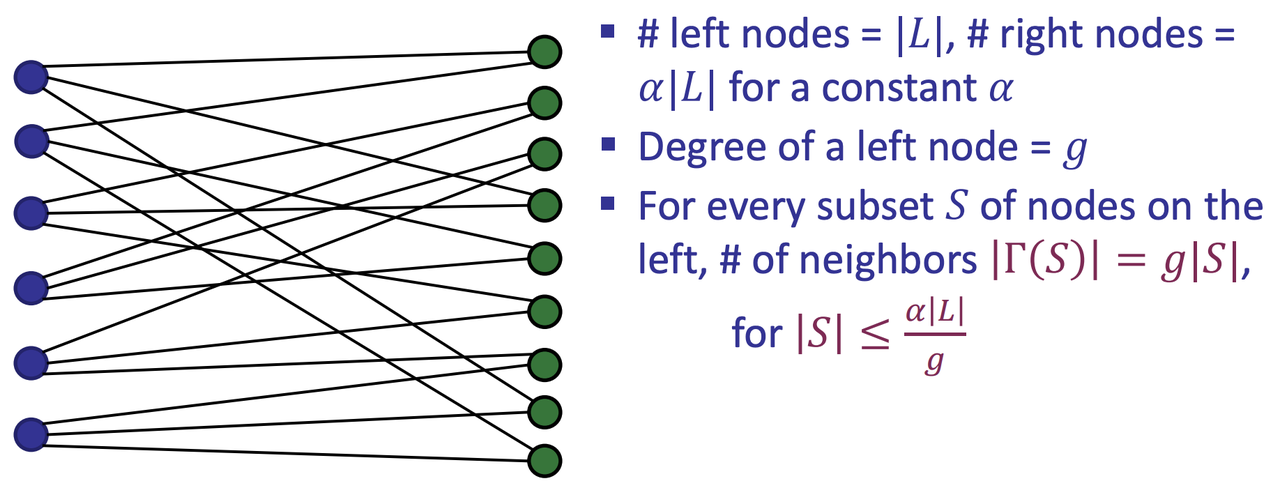
- Bi-parties graph
- Lossless Expander
- In the real definition, we just relax the conditions
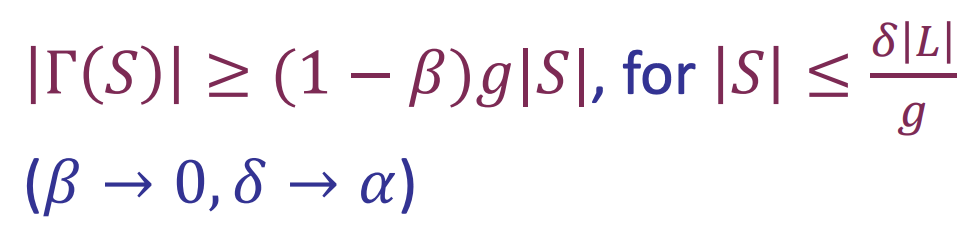
- Overview of the recursive encoding
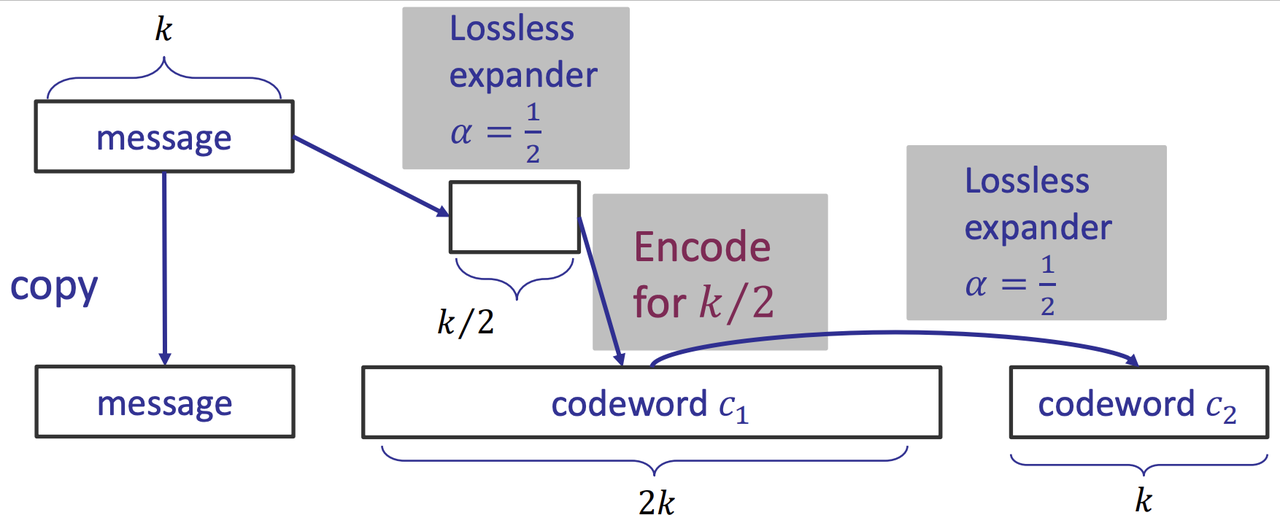
- $\Alpha = 1/2$ means the number of right nodes is the half of the left nodes.
- How to encode a 2/k message into 2k codeword $c_1$
- Recursive encoding! Use the same procedure.


- constant relative distance: $\Delta’ = min{\Delta, \frac{\delta}{4g}}$
- Proof
- Recall
- Proof
- Recursive encoding! Use the same procedure.
- Prove
- How to construct the lossless expander in practise
- [Capalbo-Reingold-Vadhan-Wigderson’2002]: Explicit construction of lossless expander (large hidden constant)
- Random sampling: 1/poly(n) failure probability
- Brakedown [Golovnev-Lee-Setty-Thaler-Wahby’21]: random summations with better concrete distance analysis
- Orion [Xie-Zhang-Song’22]: expander testing with a negligible failure probability via maximum density of the graph
- [Capalbo-Reingold-Vadhan-Wigderson’2002]: Explicit construction of lossless expander (large hidden constant)
- Putting everything together
- Polynomial commitment (and SNARK) based on linear code
- Pros:
- Transparent setup: O(1)
- Commit and Prover time: O(d) field additions and multiplications
- Plausibly post-quantum secure
- Field agnostic
- Cons:
- Proof size: O($\sqrt{d}$)