ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 9: SNARKs based on Linear PCP (Yupeng Zhang)
- SNARKs learned so far
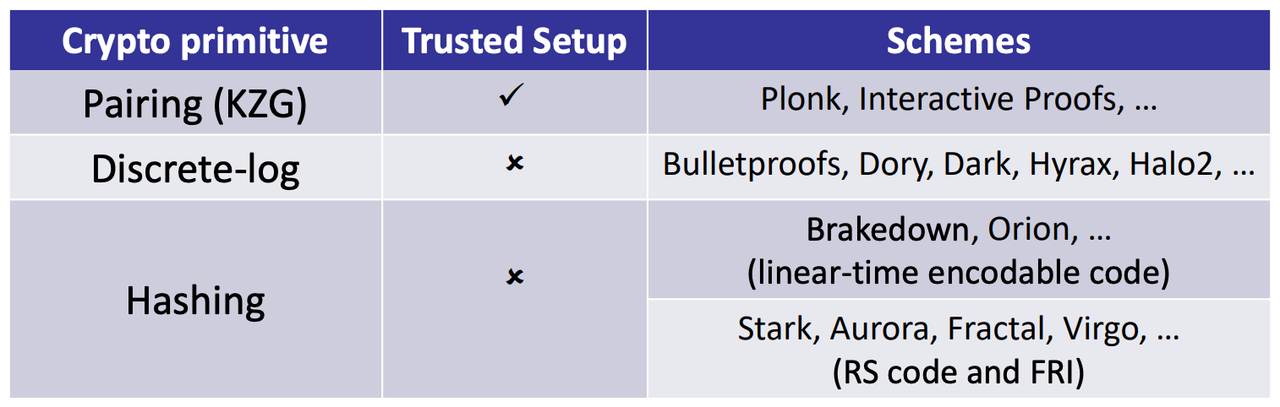
- Earliest Implemented SNARKs
- Pros
- Shortest proof size (3 elements [Groth16])
- Fast verifier (bilinear pairing)
- Cons
- FFT and group exponentiations on the prover
- Circuit-specific trusted setup
- Pros
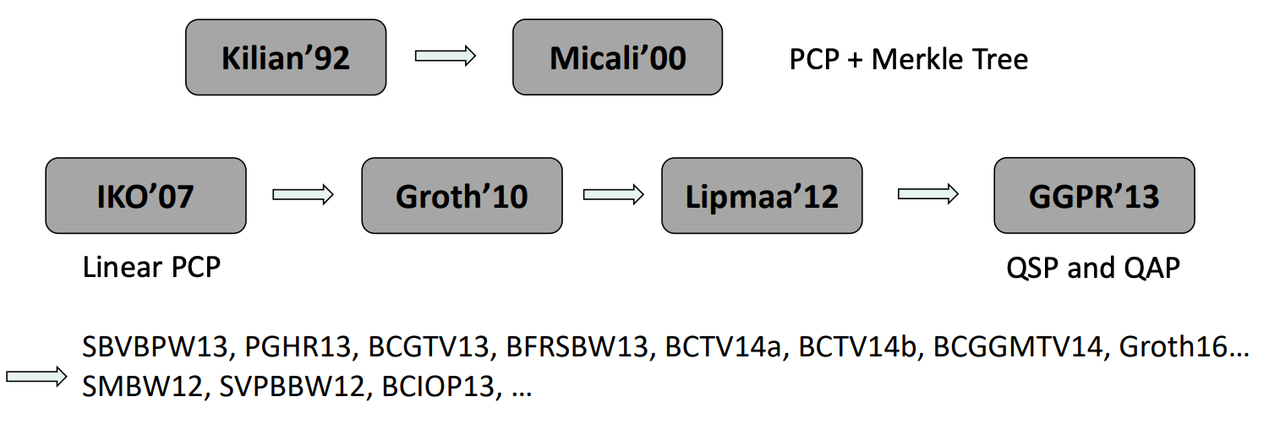
- History of SNARKs
9.1 Quadratic Arithmetic Program (QAP)
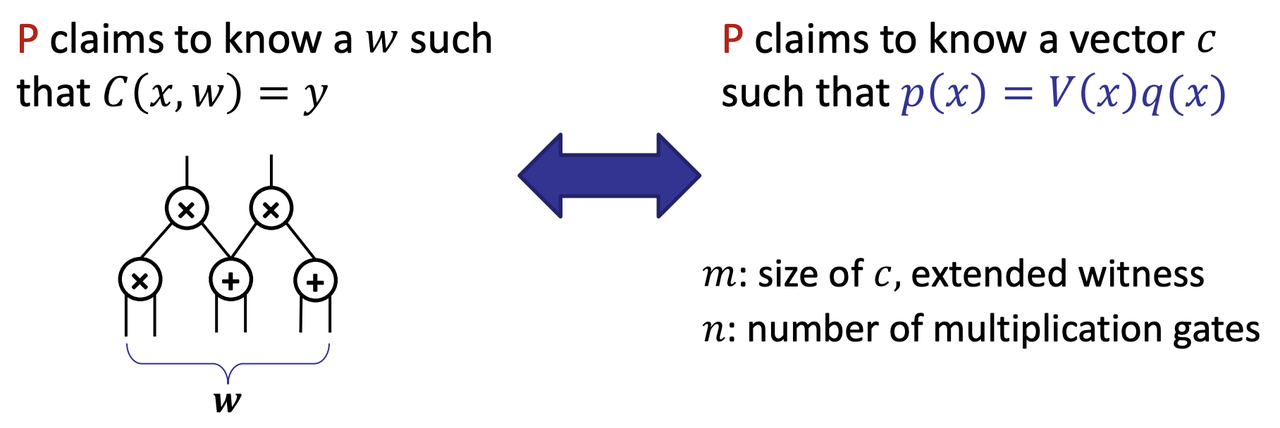
- Recall: SNARKs for circuit-satisfiability
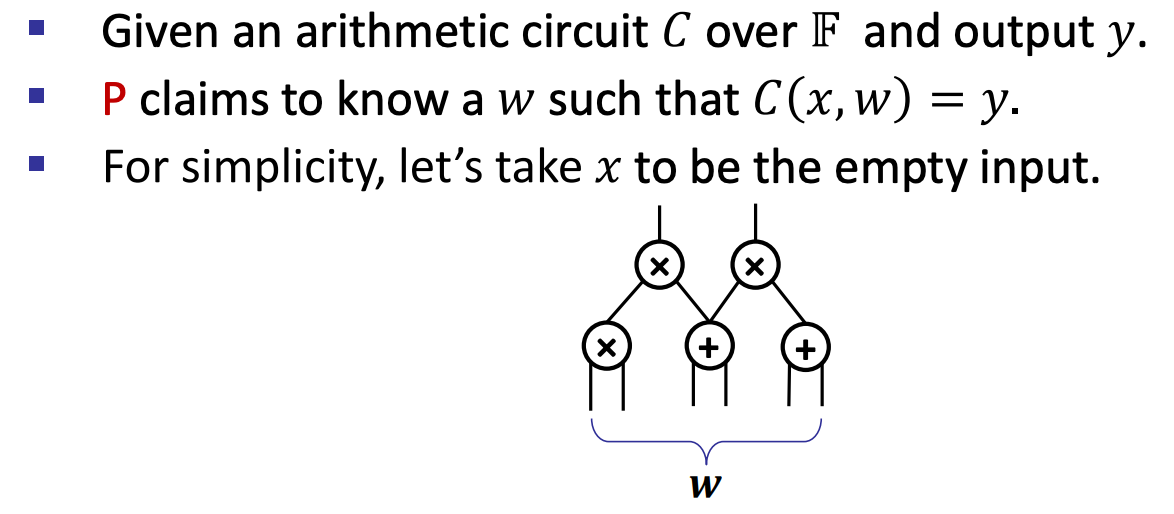
- Transcript/trace of Circuit
- Interactive proof (lecture 4, slide 76): value of every gate
- Plonk (lecture 5, slide 42): left input, right input, output of every gate
- QAP: input + output of every multiplication gate
- QAP
- Ignore the output of the addition gates
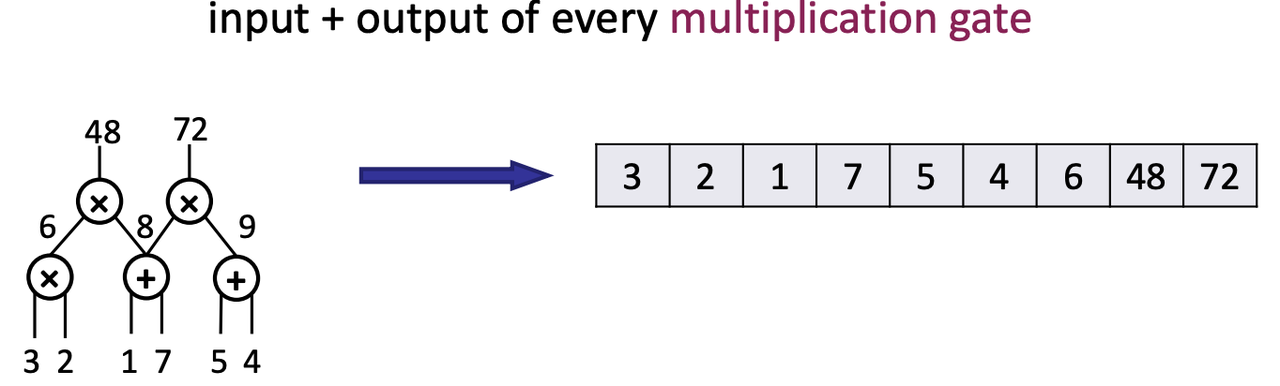
- Labeling multiplication gates
- Selector Polynomials
- $l_i(x)$: is $c_i$ the left input of gate 𝑗, for 𝑗 = 1,2,3?
- Examples:
- $l_i(x)$: is $c_i$ the left input of gate 𝑗, for 𝑗 = 1,2,3?
- Ignore the output of the addition gates

For $l_1(x)$:
- 3 is the left input of gate 1? Yes! -> 1
- 3 is the left input of gate 2? No! -> 0
- 3 is the left input of gate 3? No! -> 0
For $l_3(x)$:
- 1 is the left input of gate 1? No! -> 0
- 1 is the left input of gate 2? No! -> 0
- 1 is the left input of gate 3?
- Yes! -> 1
- Because “1” is the input of the addition gate, and the addition gate is the left input of gate 3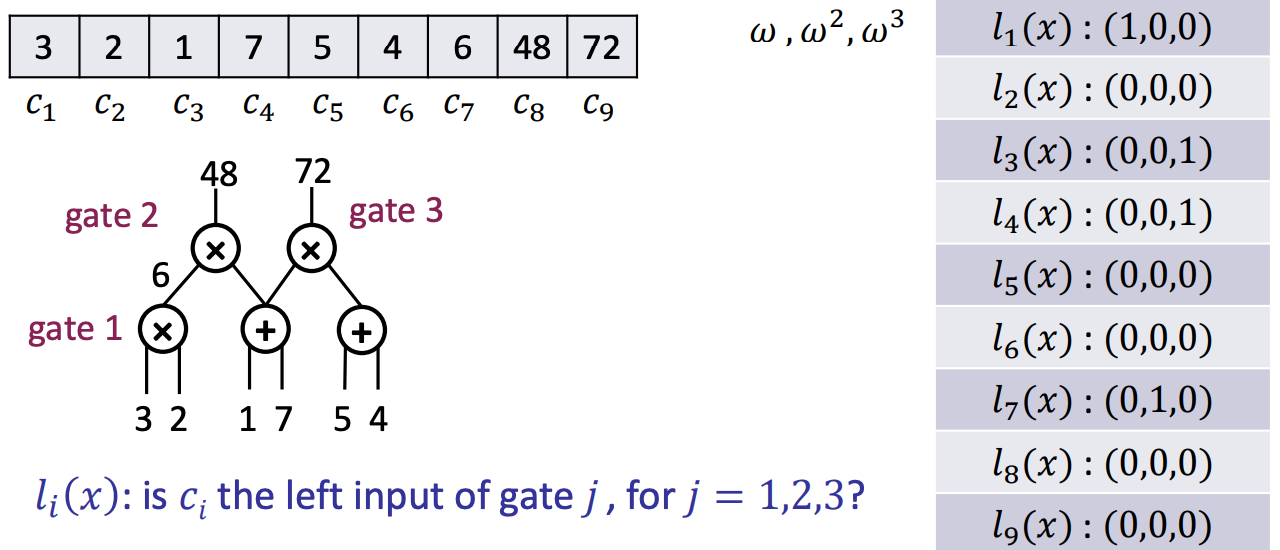
- Properties of the selector polynomials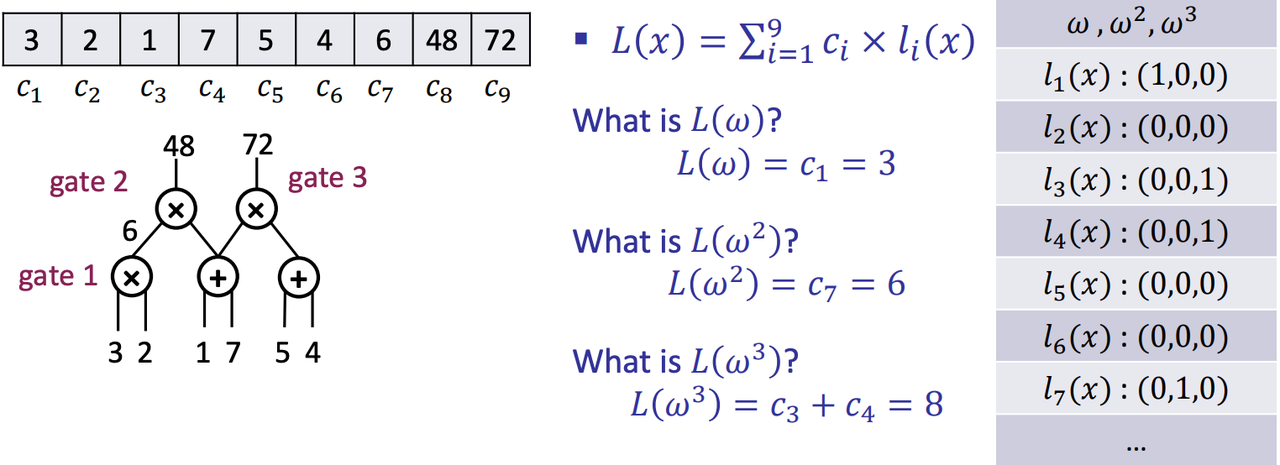
- More Selector Polynomials
- $r_i(x)$: is $c_i$ the right input of gate 𝑗, for 𝑗 = 1,2,3?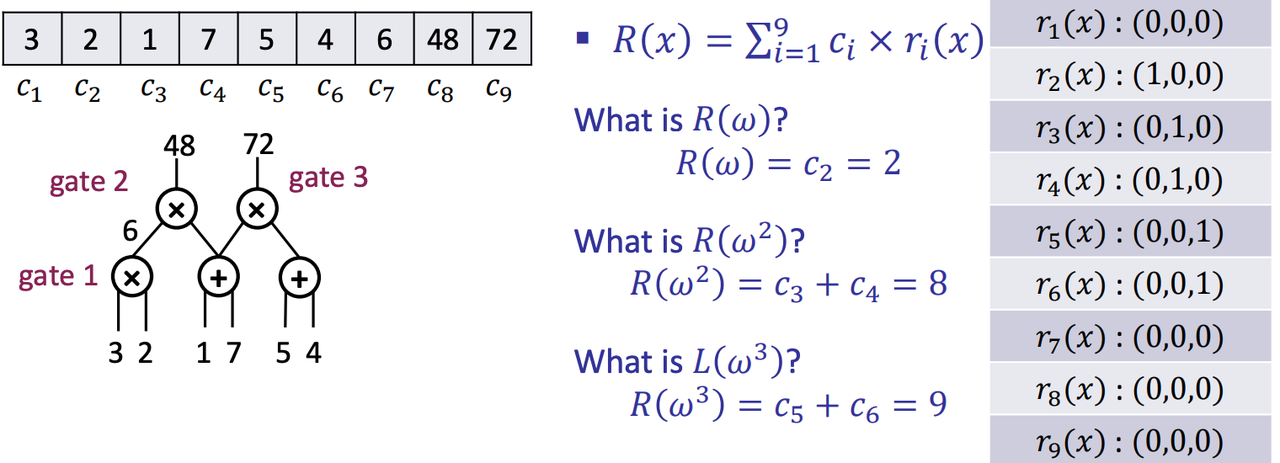
- $o_i(x)$: is $c_i$ the output of gate 𝑗, for 𝑗 = 1,2,3?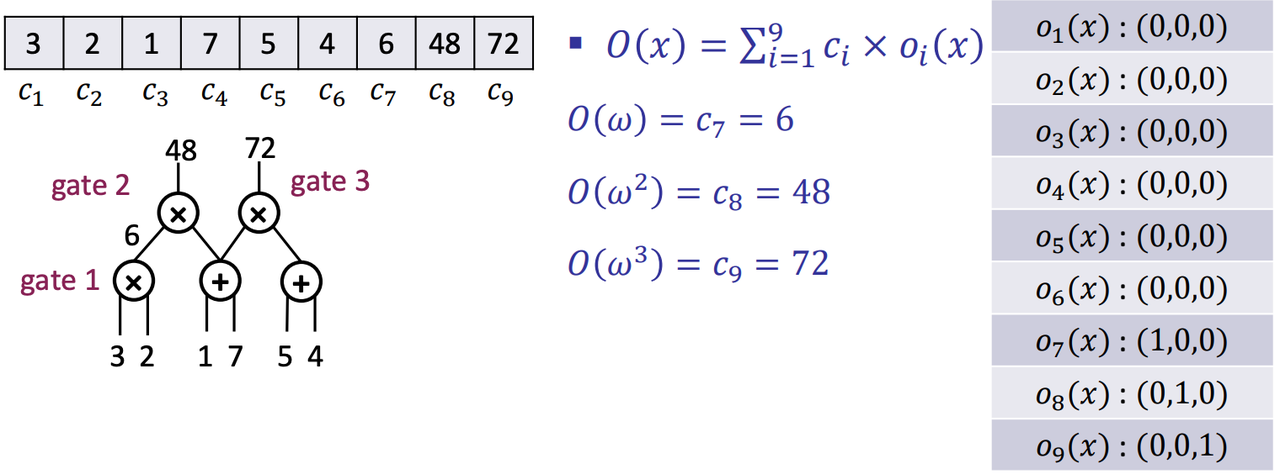
- Master polynomial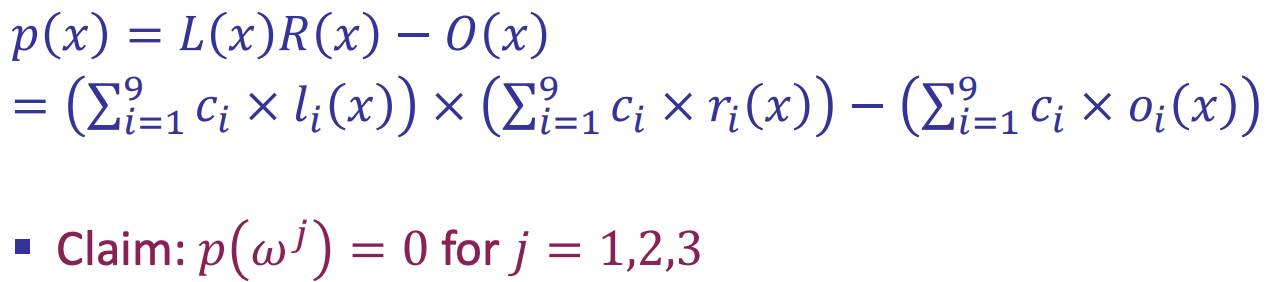
- Vanishing polynomial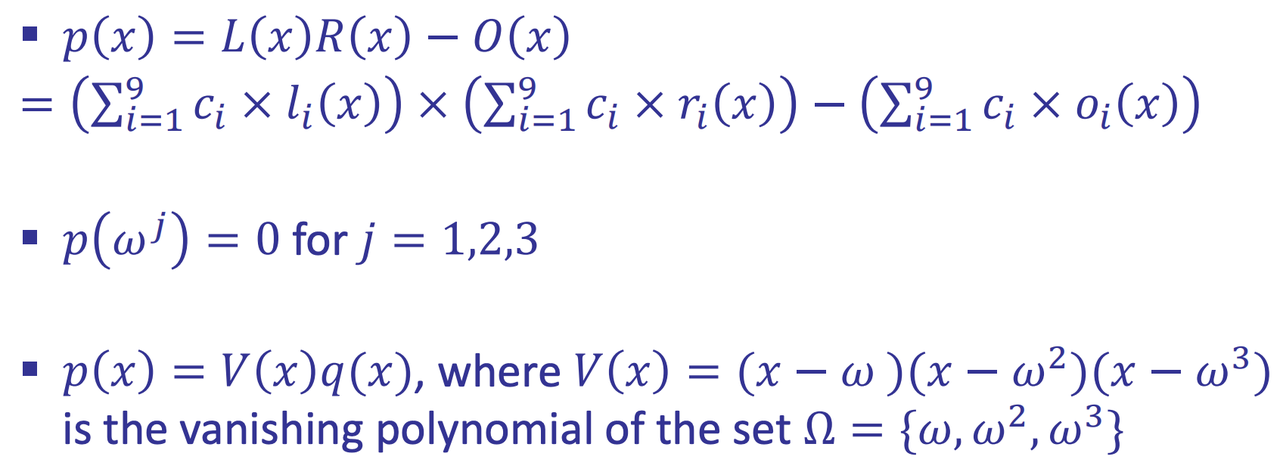
- Circuit-SAT to QAP [GGPR13, PGHR13]
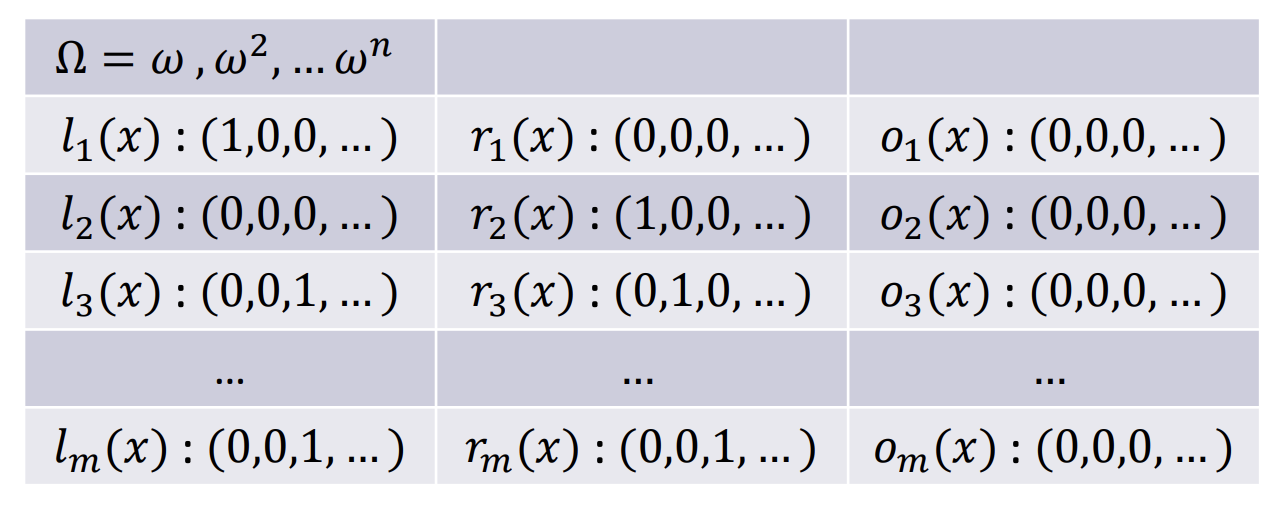
- The table is sparse.
9.2 From QAP to SNARK
- Probabilistically Checkable Proofs (PCP)
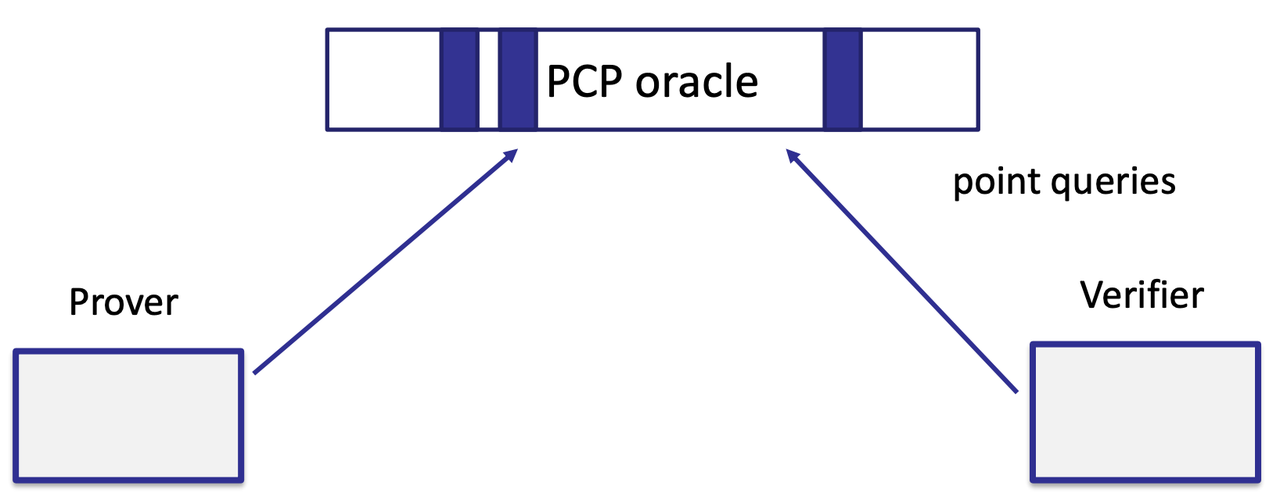
- IPCP [Kalai-Raz’08] and IOP [Ben-Sasson-Chiesa-Spooner’16]
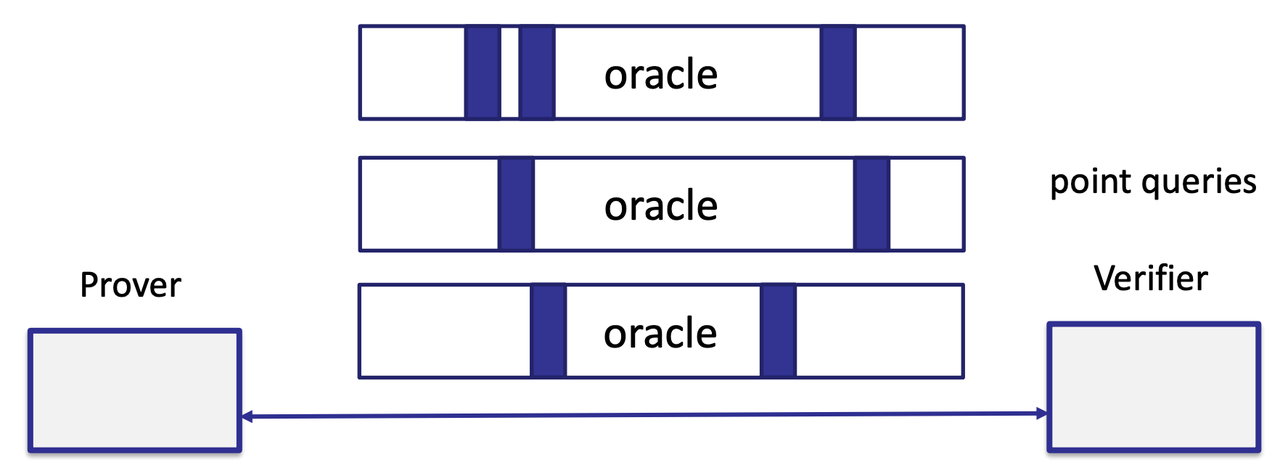
- Polynomial IOP [Bünz-Fisch-Szepieniec’20]
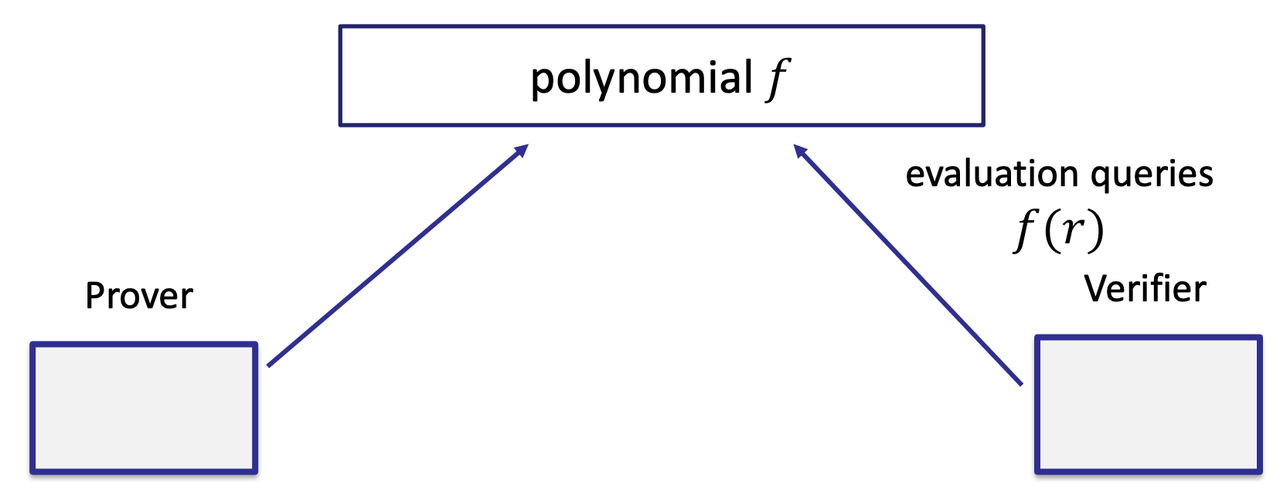
- Linear PCP [Ishai-Kushilevitz-Ostrovsky’07]
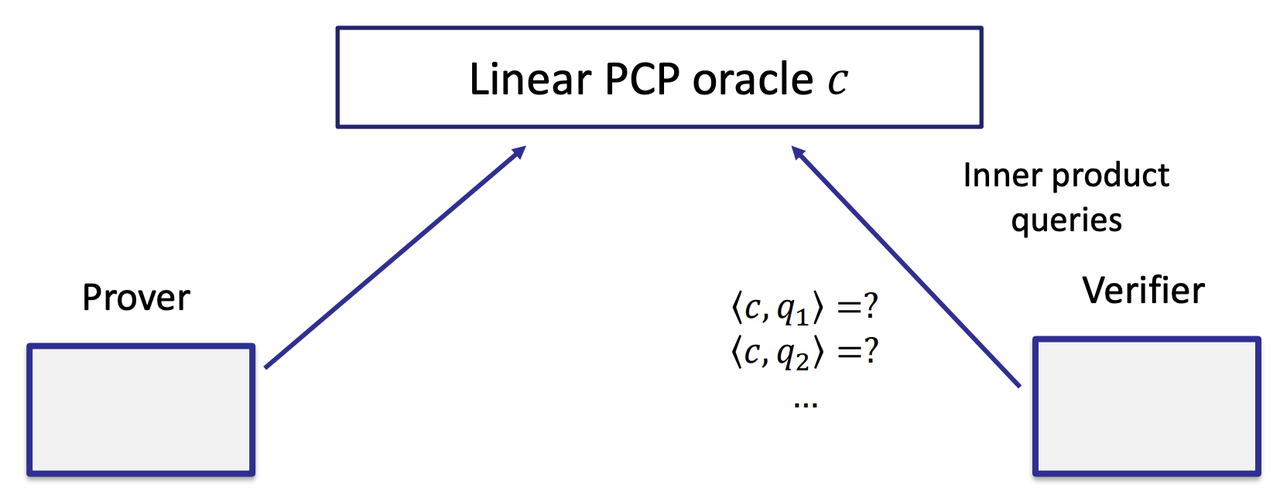
- QAP and Linear PCP

- We don’t use random checks.
- Key Generation
- The $c_i$ and $q(x)$ are private
- The selector polynomials and the vanishing polynomial are public.
- The circuit can be pre-processed. (The preprocessing phase is circuit-dependent)

- Prove

- Verify

- Towards the real protocol
- Q1: How to make sure $\pi_1$ is computed from $g^{l_i(\tau)}$
- Solution: Knowledge of Exponent assumption (KoE) or Generic Group Model (GGM)
- Recall: KoE
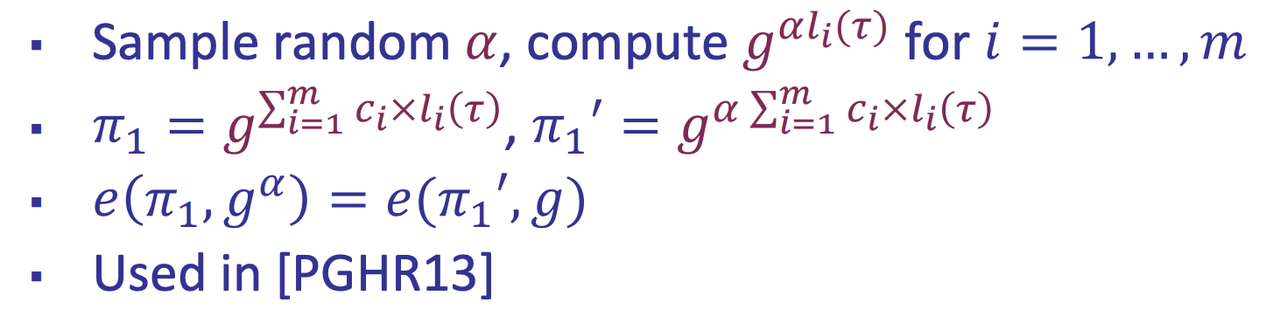
- Recall: GGM

- Q2: how to make sure the same $c$ is used in $\pi_1$,$\pi_2$ and $\pi_3$?
- Solution
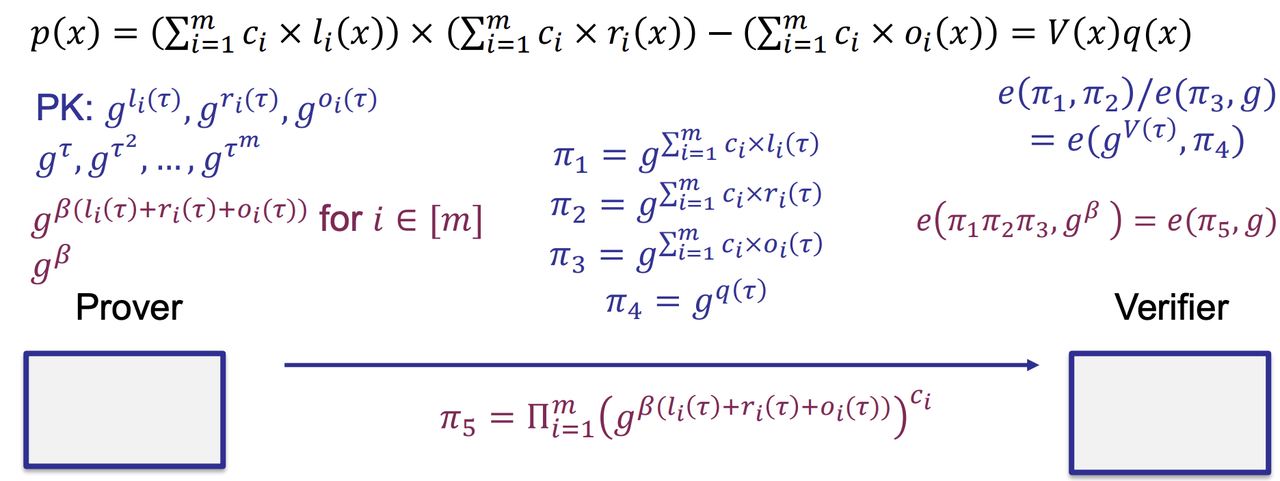
- Solution
- Q3: What about public input and output?
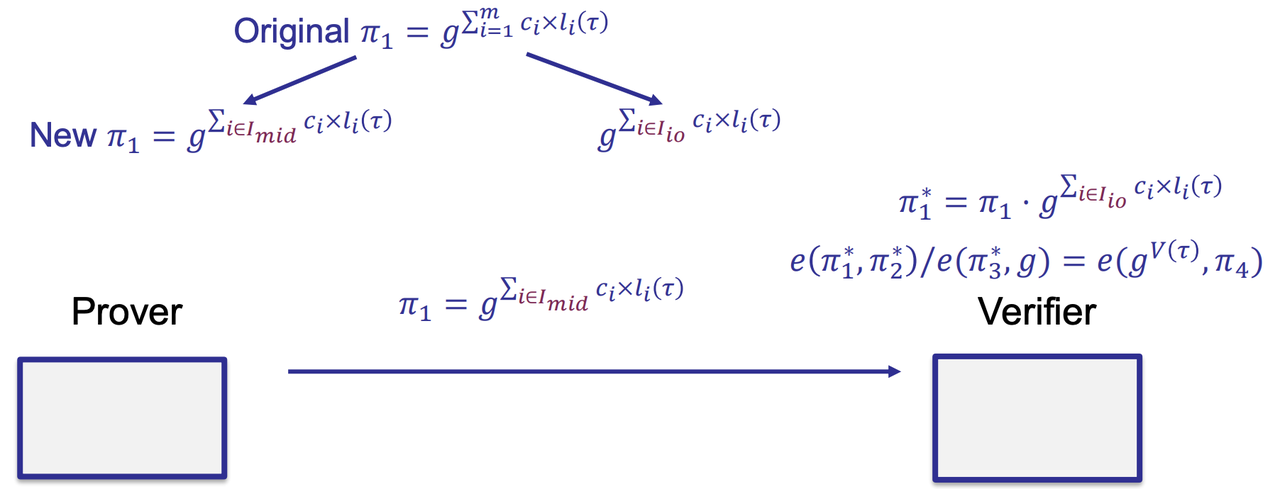
- $I_{mid}$: secret witness
- $I_{io}$: public input and public output
- Q1: How to make sure $\pi_1$ is computed from $g^{l_i(\tau)}$
- Putting everything together
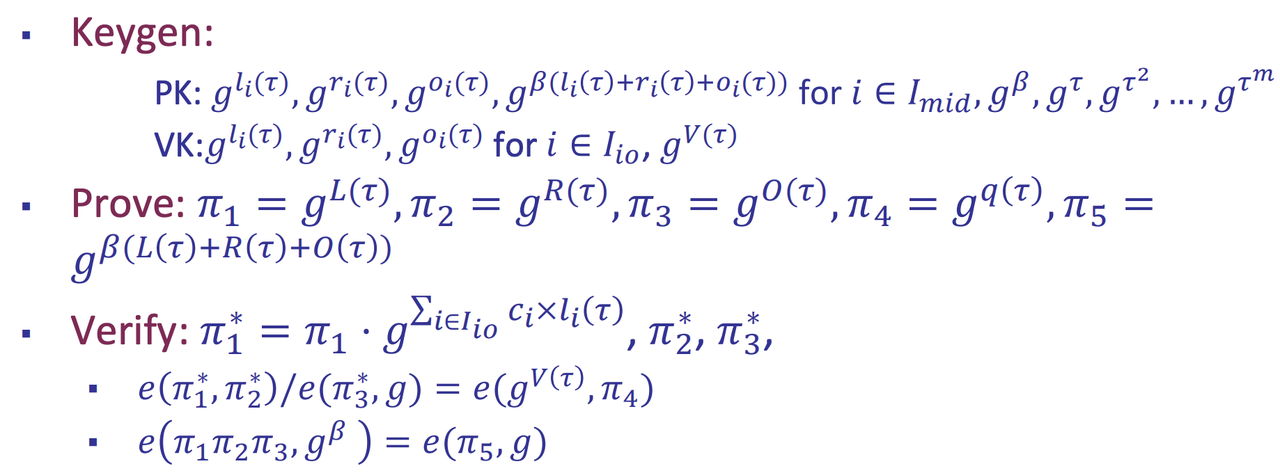
- Properties of SNARK [PGHR13]

9.3 Other variants
- Rank-1-Constraint-System (R1CS)
- QAP

- R1CS:
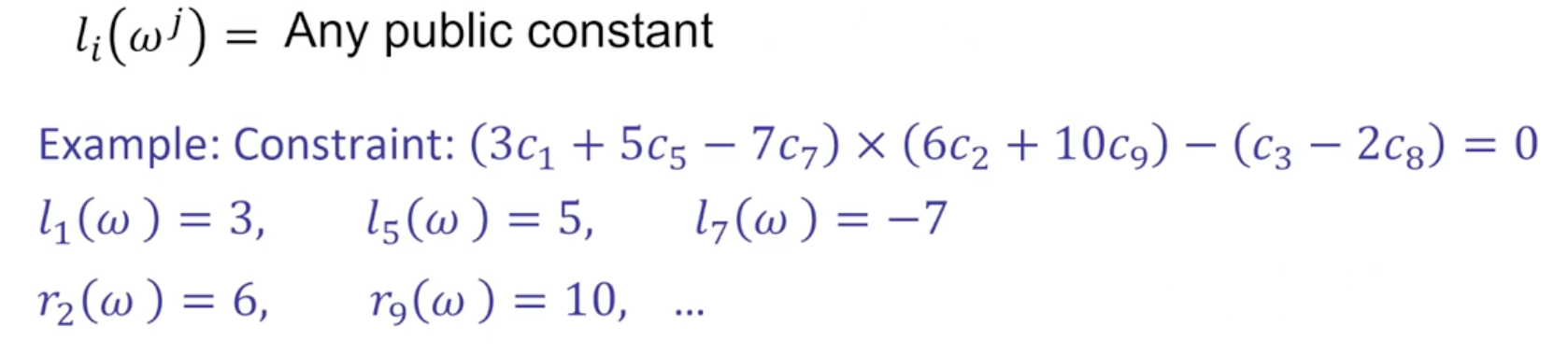
- Advantages
- Can support generalized constraints or gates
- more convenient to use in practice
- Matrix View of R1CS
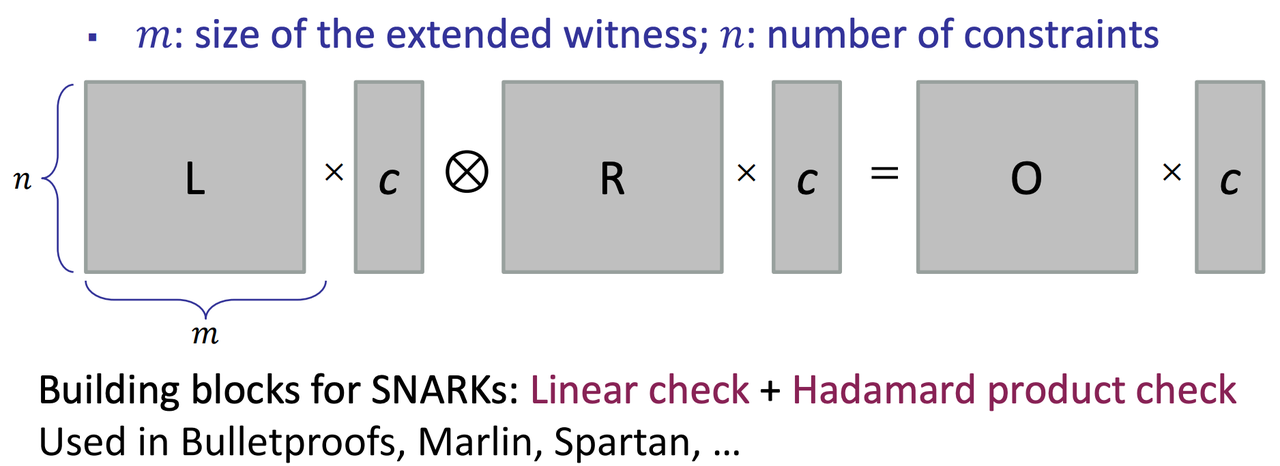
- Advantages
- QAP
- Groth16
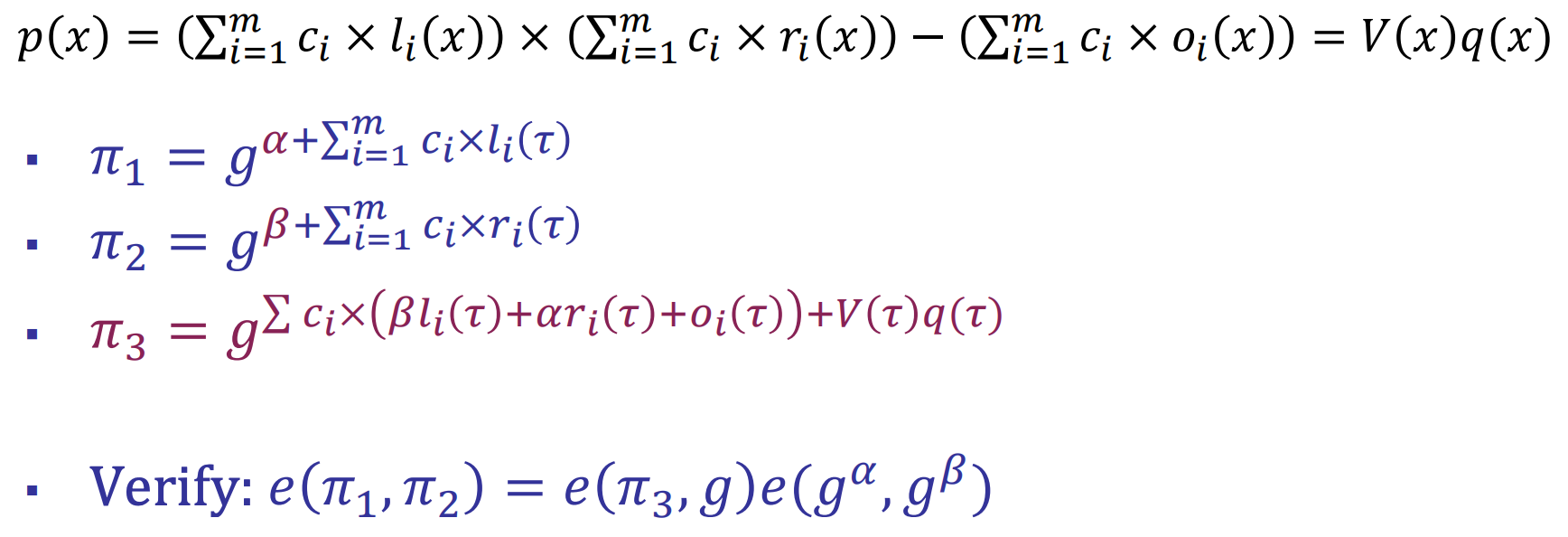
- Combine the $\pi_3$, $\pi_4$, $\pi_5$ of [PGHR13] together
- $\alpha$ and $\beta$ are secret keys in the trusted key generation, and $g^\alpha$ and $g^\beta$ are public parameters for the prover and the verifier
- $\pi_3$: move the $\Sigma_{i=1}^m c_i \times o_i(x)$ to the right side of the equation -> $\Sigma_{i=1}^m c_i \times o_i(x) + V(x)q(x)$
- Change the keygen accordingly
- Proof size: 3 group elements, 144 bytes
- Verifier time: 1 pairing equation
- Combine the $\pi_3$, $\pi_4$, $\pi_5$ of [PGHR13] together
- Achieving Zero-Knowledge
- The above is not zero-knowledge, because the adversary can infer some information by brute force attack.
- Solution: add some random values (times the vanishing polynomial)
- The [PGHR13] version:

- The [PGHR13] version: