ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 10: Recursive SNARKs, Aggregation and Accumulation (Dan Boneh)
10.1 Introduction and Applications of Recursive SNARKs
- Recall: SNARK algorithms
- A preprocessing SNARK is a triple (S, P, V):
- $S(C)$ -> public parameters (pp, vp) for prover and verifier
- $P(pp, x, w)$ -> proof $\pi$
- $V(vp, x, \pi)$ -> accept or reject
- A preprocessing SNARK is a triple (S, P, V):
- SNARK types
- Groth16, Plonk-KZG: short proofs, but prover time is O(n log n)
- FRI-based proofs (as well as Breakdown, Orion, Orion+, …): faster prover, but longer proofs
- Two level SNARK recursion: proving knowledge of a proof
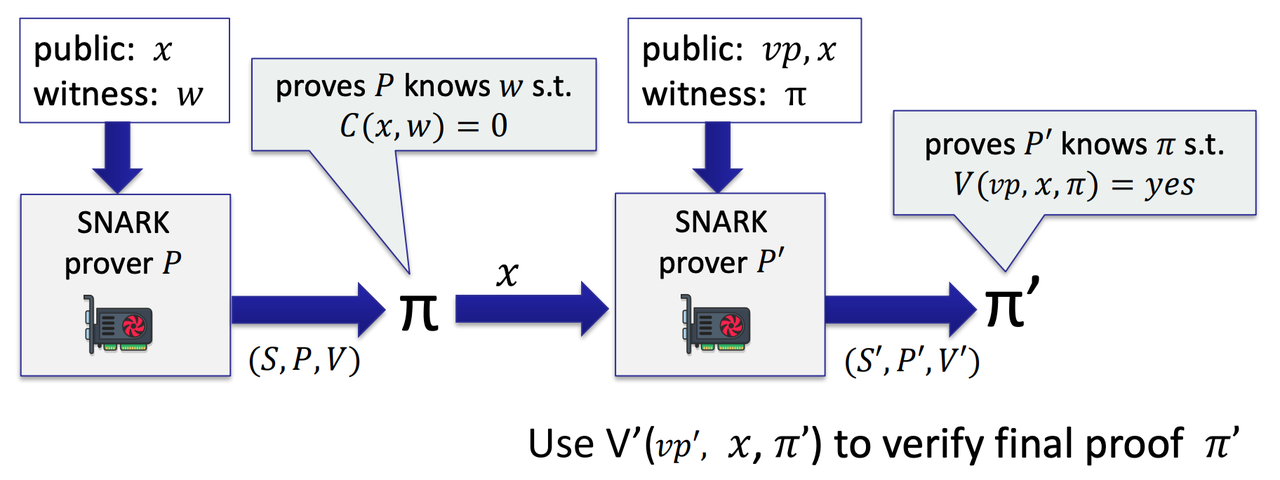
- Inner proof: prove P knows w
- Outer proof: prove P’ knows $\pi$
- Application
- proof compression
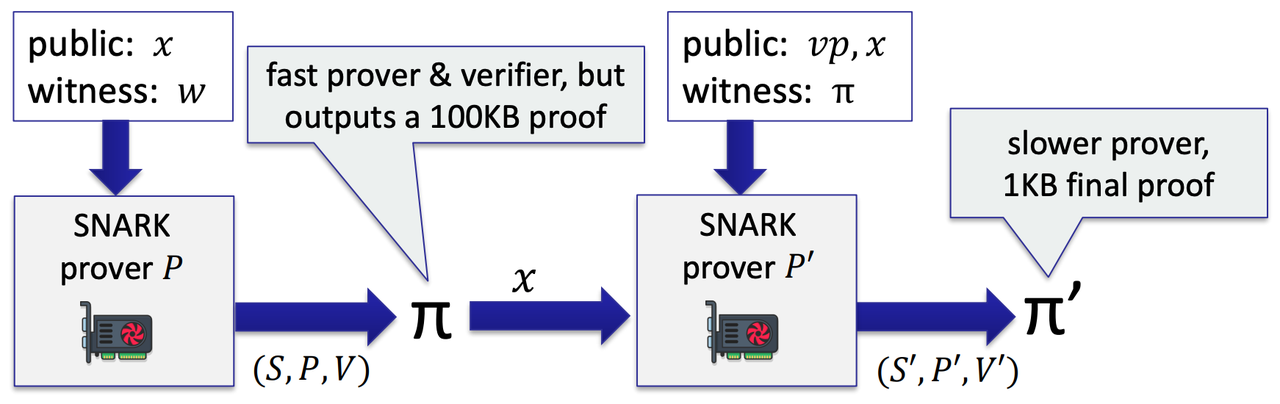
- fast overall prover, and final proof is short(used to prove complex statements)
- Knowledge sound

- Another difficulty: random oracles

- streaming proof generation

- zk-Rollup
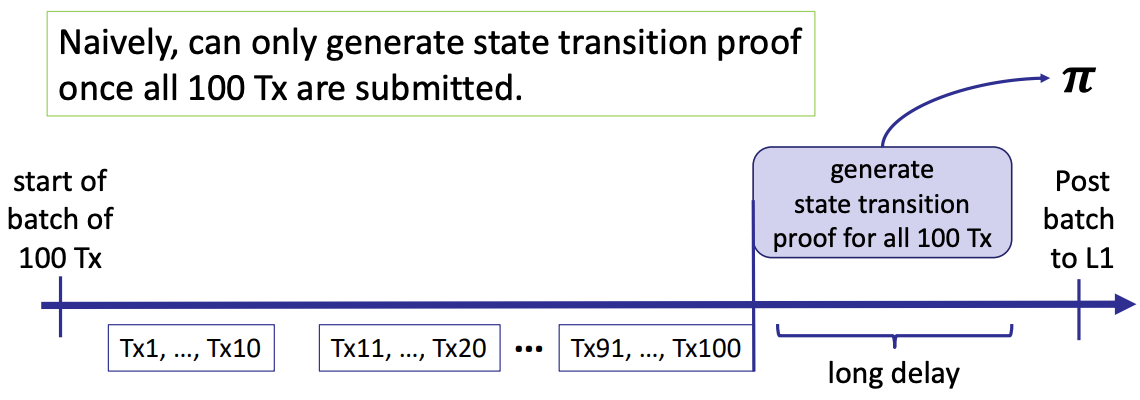
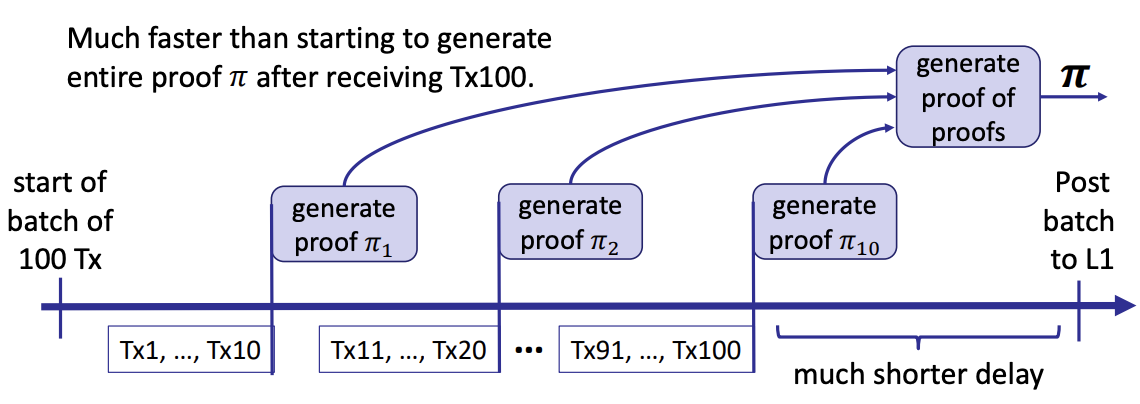
- zk-Rollup
- Layer-3 zk-Rollups
- Incrementally Verifiable Computation (IVC)
- Incrementally Verifiable Computation or Proofs of Knowledge Imply Time/Space Efficiency [Valiant’08]
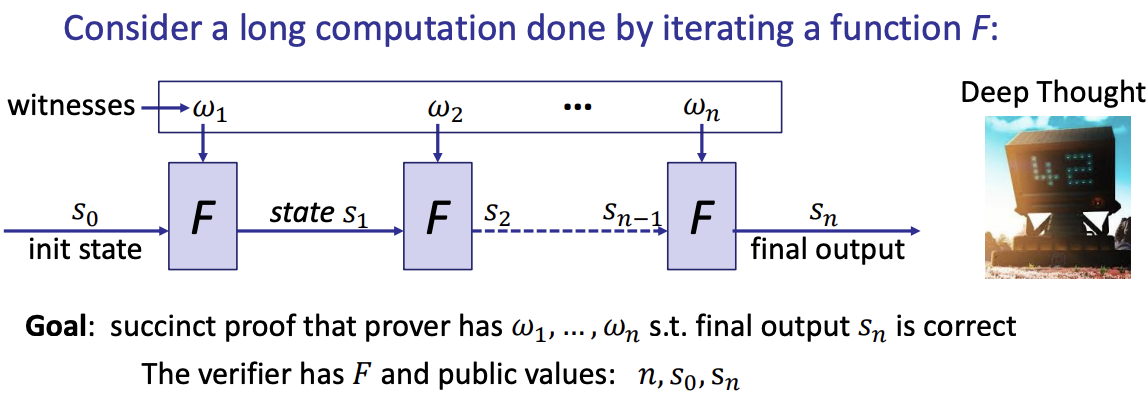

- The statement at step number i
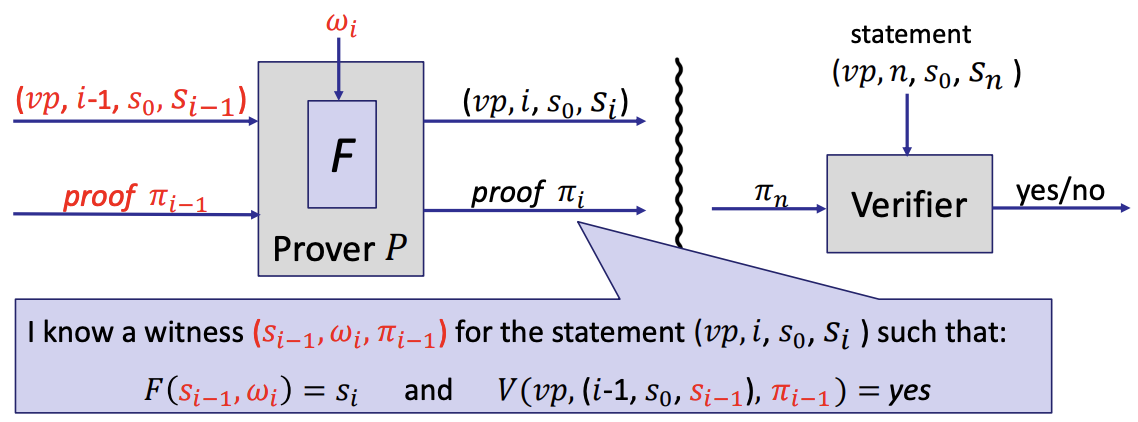
- Applications of IVC
- Break a long computation into a sequence of small steps
- F: one microprocessor step (Risc5, EVM, …)
- Prover needs far less memory per step compared to a monolithic proof
- A succinct proof that the current state of blockchain is correct
- Break a long computation into a sequence of small steps
- Incrementally Verifiable Computation or Proofs of Knowledge Imply Time/Space Efficiency [Valiant’08]
- proof compression

- Verifiable Delay Functions (VDF): succinct proof that $s_n$ is equal to $H^{(n)}(s_0)$
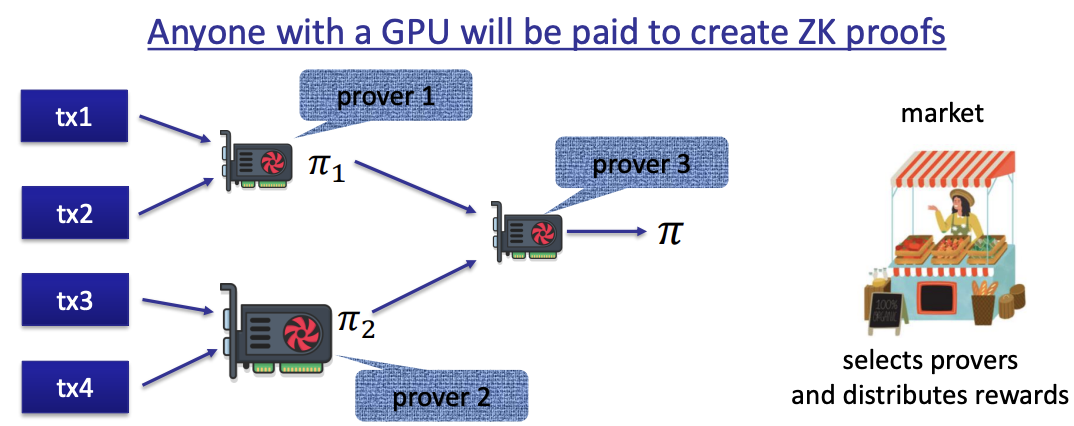
- Application 5: a market for ZK provers
10.2 Choosing Curves to Support Recursion
- Recursive SNARK

- Algebraic Groups

- $F_q^l$: an element $F_q^l$ is a $l$ elements tuple of $F_q$
- Recursive proofs: the arithmetic problem
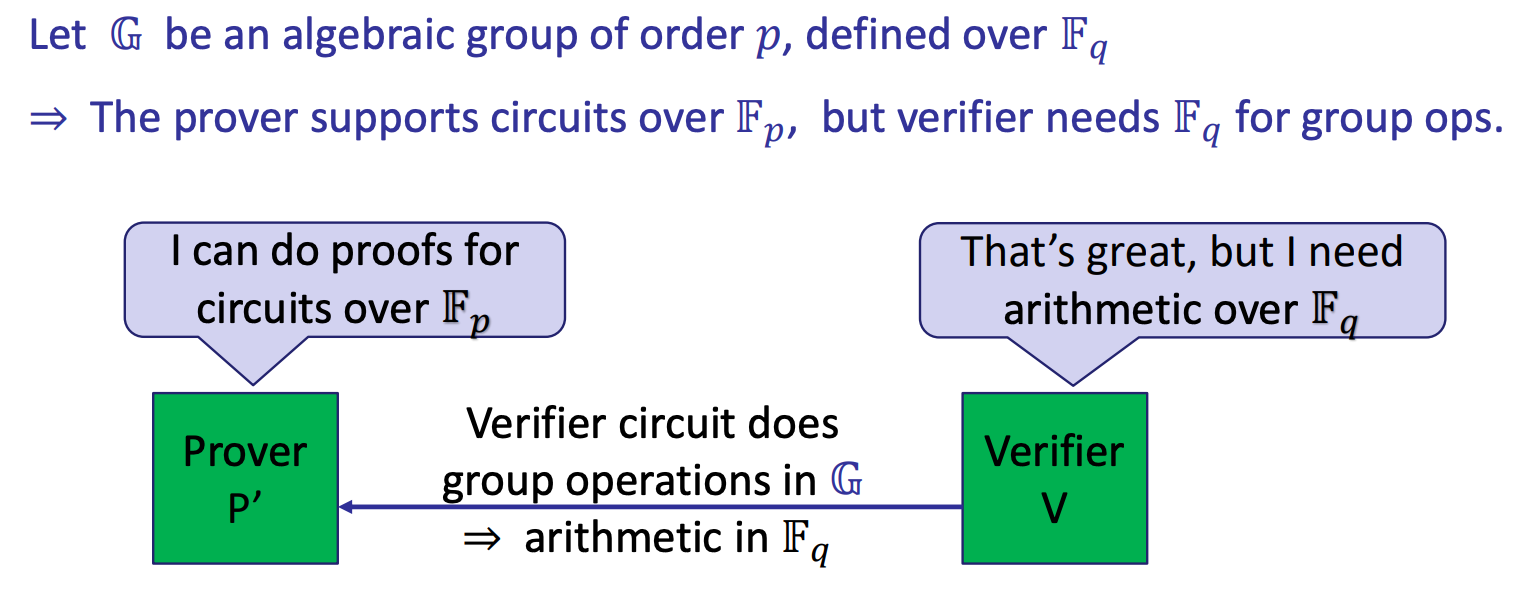
- What to do?

- Solution: a chain of groups


- Even better: a cycles of groups [BCTV’14]

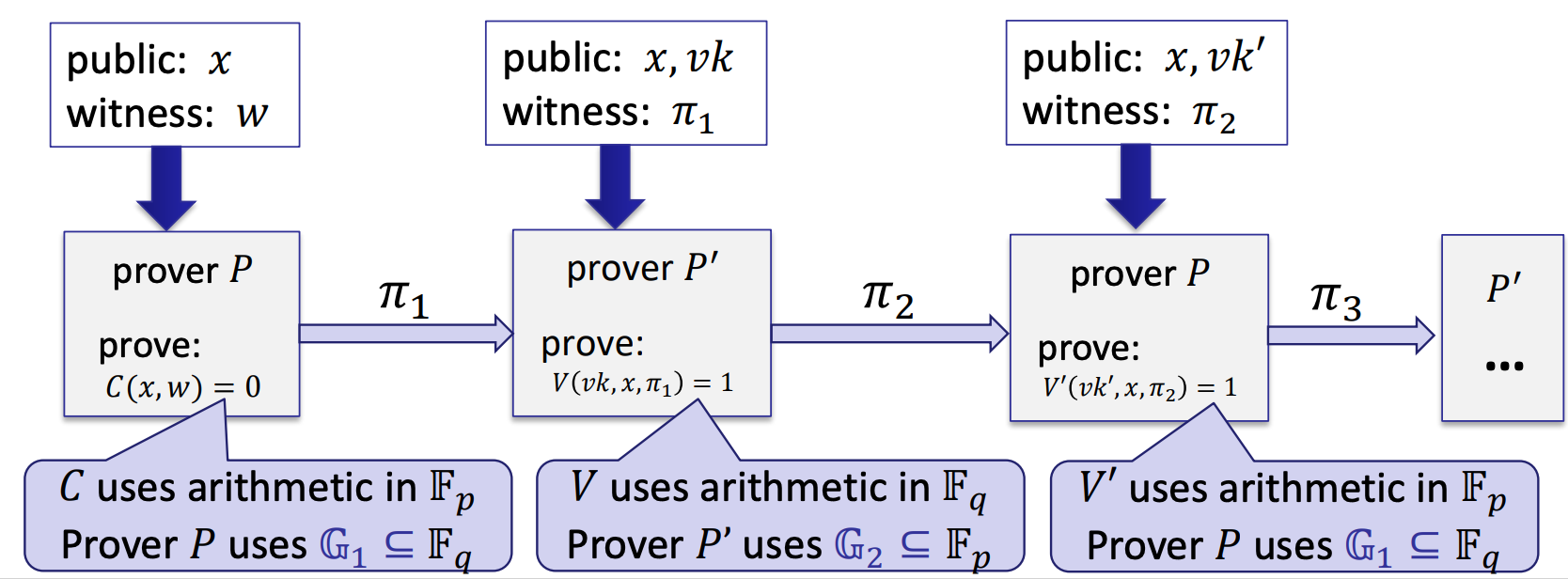
- Three types of cycles of length two


- What to do?