ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 8: FRI-based Polynomial Commitments and Fiat-Shamir (Justin Thaler)
8.1 Polynomial-IOP and Polynomial Commitment Schemes
- Recall: build an efficient SNARK
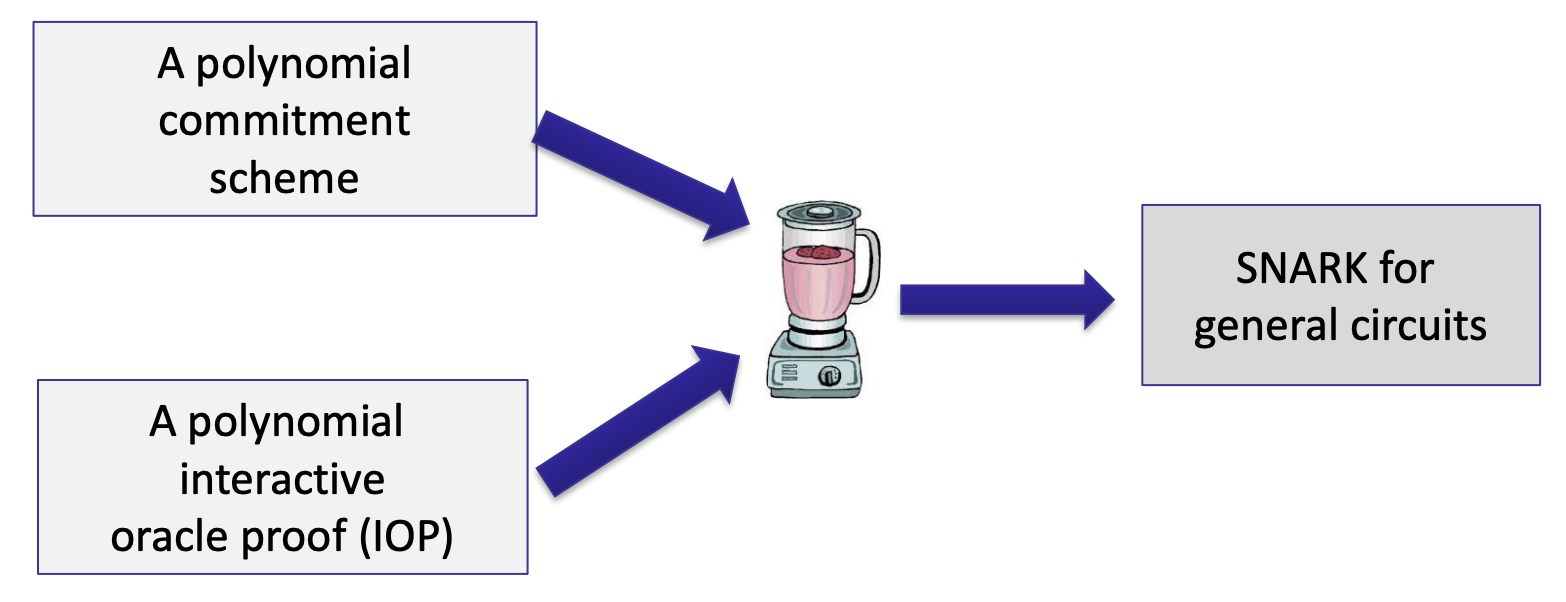
- Recall: Polynomial-IOP
- P’s first message in the protocol is a polynomial h.
- V does not learn h in full.
- The description size of h is as large as the circuit
- Rather, V is permitted to evaluate h at one point.
- After that, P and V execute a standard interactive proof.
- Recall: Polynomial Commitment Scheme
- High-level idea:
- P binds itself to a polynomial h by sending a short string Com(h)
- V can choose x and ask P to evaluate h(x)
- P sends y, the purported evaluation, plus a proof $\pi$ that y is consistent with Com(h) and x.
- Goals:
- P cannot produce a convincing proof for an incorrect evaluation.
- Com(h) and $\pi$ are short and easy to generate; $\pi$ is easy to check.
- High-level idea:
- Recall: Three classes of Polynomial IOPs
- Based on interactive proofs (IPs)
- Based on multi-prover interactive proofs (MIPs)
- Based on constant-round polynomial IOPs
- Examples: Marlin, PlonK.
- Recall: Three classes of Polynomial commitments
- Based on pairings + trusted setup (not transparent nor post-quantum)
- e.g., KZG10
- Unique property: constant sized evaluation proofs
- Based on discrete logarithm (transparent, not post-quantum)
- Examples: IPA/Bulletproofs, Hyrax, Dory
- Based on IOPs + hashing (transparent and post-quantum)
- e.g., FRI, Ligero, Brakedown, Orion
- Note:
- Classes 1. and 2. are homomorphic.
- Leads to efficient batching/amortization of P and V costs (e.g., when proving knowledge of several different witnesses).
- The three classes are listed in an increasing verification cost.
- Classes 1. and 2. are homomorphic.
- Based on pairings + trusted setup (not transparent nor post-quantum)
- Highlights of SNARK Taxonomy
- Transparent SNARKs
- [Any polynomial IOP] + IPA/Bulletproofs polynomial commitment.
- Ex: Halo2-ZCash
- Pros: Shortest proofs among transparent SNARKs
- Cons: Slow V (linear time)
- [Any polynomial IOP] + FRI polynomial commitment.
- Ex: STARKs, Fractal, Aurora, Virgo, Ligero++
- Pros:
- Shortest proofs amongst plausibly post-quantum SNARKs.
- More flexibility for what field you work over
- Cons: Proofs are large (100s of KBs depending on security)
- MIPs and IPs + [fast-prover polynomial commitments].
- Ex: Spartan, Brakedown, Orion, Orion+(HyperPlonk)
- Pros: Fastest P in the literature, plausibly post-quantum + transparent if polynomial commitment is.
- Cons: Bigger proofs than 1. and 2. above
- [Any polynomial IOP] + IPA/Bulletproofs polynomial commitment.
- Non-transparent SNARKS
- Linear-PCP based:
- Ex: Groth16
- Pros: Shortest proofs (3 group elements), fastest V.
- Cons: Circuit-specific trusted setup, slow and space-intensive P, not postquantum
- Constant-round polynomial IOP + KZG polynomial commitment:
- Ex: Marlin-KZG, PlonK-KZG
- Pros: Universal trusted setup.
- Cons: Proofs are ~4x-6x larger than Groth16, P is slower than Groth16, also not post-quantum.
- Counterpoint for P: can use more flexible intermediate representations than circuits and R1CS.
- Linear-PCP based:
- Transparent SNARKs