ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 11: From Practice to Theory (Guest Lecturer: Alex Lombardi)
11.2 Fiat-Shamir and SNARGs
- Succinct Non-Interactive Arguments (SNARGs)

- This class so far: constructions of SNARGs using IOPs and a random oracle.
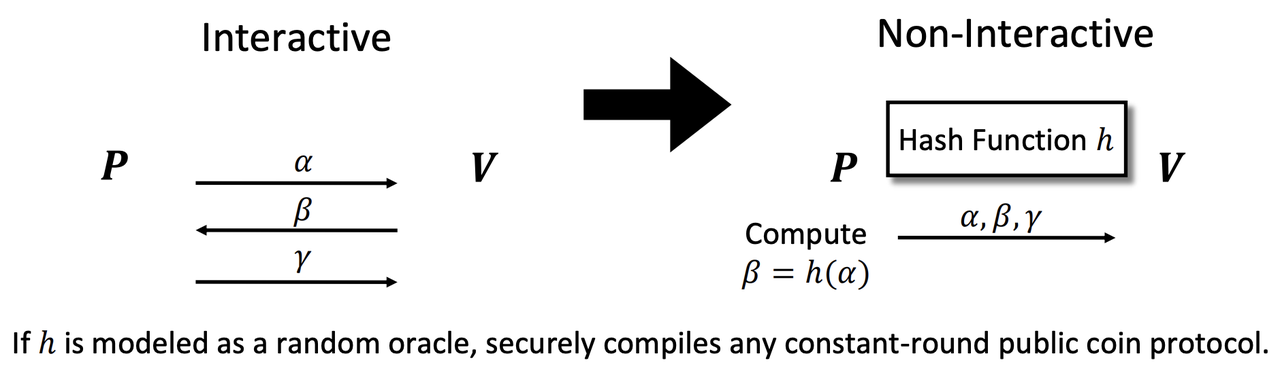
- The Fiat-Shamir Transform
- Powerful, general proposal for removing interaction
- The Random Oracle Model [BR93]
- Assumption about the structure of an attack on a hash function h
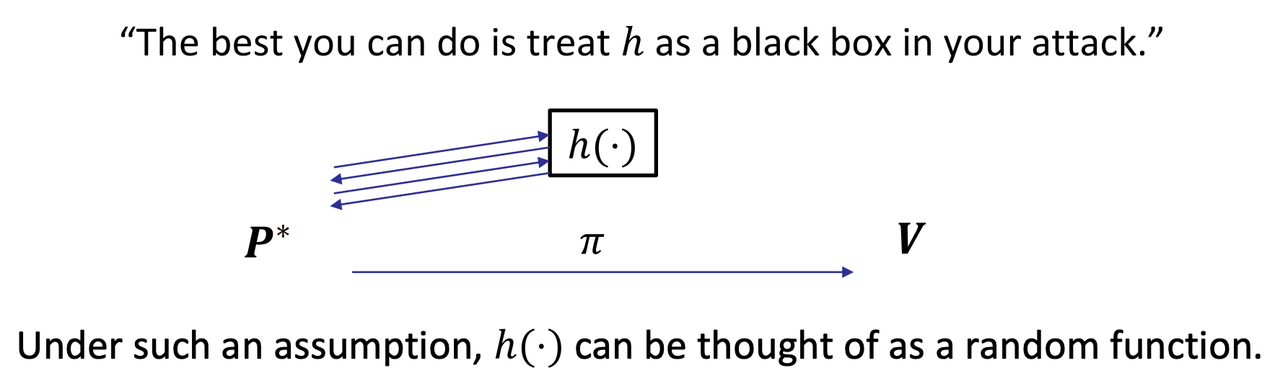
- Assumption about the structure of an attack on a hash function h
- Fiat-Shamir in the ROM (Random Oracle Model)
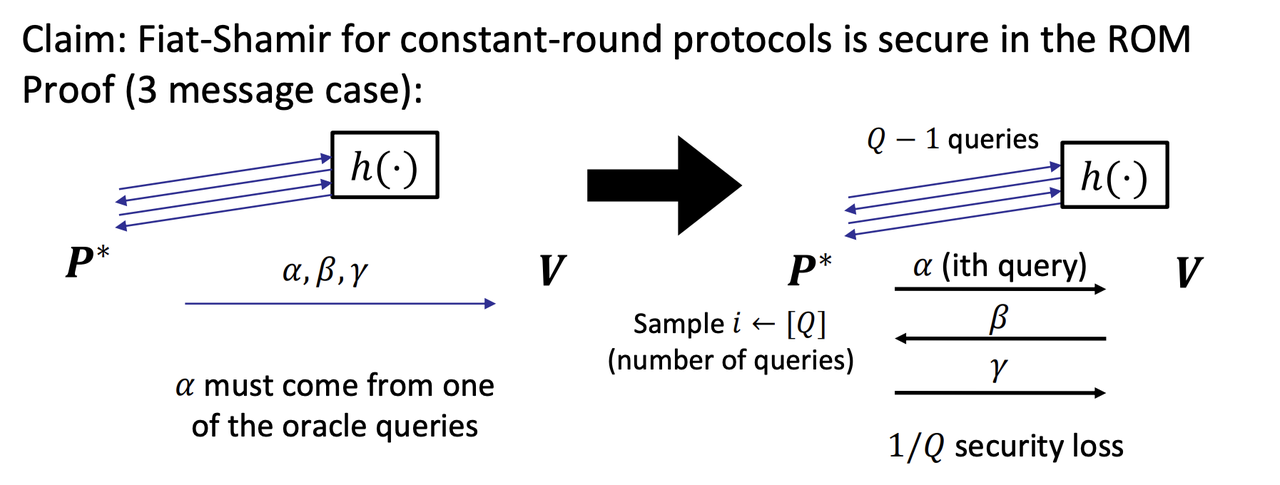
- Under such an assumption, h() can be thought of as a random function.
- In practice, h() is instantiated with (e.g.) SHA256, possibly salted.
- No matter what, h() is instantiated with a public efficient algorithm
- Powerful, general proposal for removing interaction
- Obvious (theoretical) problem: Public efficient algorithms can’t compute random functions
- Example of an uninstantiable random oracle property [CGH98]
- Random Oracles Do Not Exist

- For any fixed f, a RO is CI for f.
- Why? Each query x to the RO produces a random output y, which is equal to f(x) with probability $2^{-\lambda}$.

- Is this a reasonable counterexample?
- Hash function/random oracle must be able to hash inputs of arbitrary length. CI with bounded inputs might exist!
- [Barak01,GK03] apply to fixed-input length hash functions.
- Theorem [Barak ‘01, Goldwasser-Kalai ‘03]: $\exsit$ interactive protocol $\Pi$ such that $\Pi_{FS}$ is ROM-secure but insecure for any efficiently computable H (e.g. SHA-3).
- Security property broken by running the hash function on its own description. Is this practically relevant?
- Recursive SNARKs do something of this flavor
- Does NOT imply RO-based SNARKs are broken in practice.
- But it does imply a lack of theoretical understanding.
- Random Oracles Do Not Exist
- Example of an uninstantiable random oracle property [CGH98]