ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 11: From Practice to Theory (Guest Lecturer: Alex Lombardi)
11.3 What can we do without random oracle model
- Falsifiable Assumptions
- Prove security assuming that some concrete algorithmic task is infeasible:
- Computing discrete logarithms is hard.
- Solving random noisy linear equations (LWE) is hard.
- SHA256 is collision-resistant
- Many cryptographic constructions use random oracles to get better efficiency, but can be based on falsifiable assumptions.
- CCA-secure public key encryption
- Identity-based encryption.
- Non-interactive zero knowledge
- Can (ZK-)SNARKs for NP be built based on falsifiable assumptions?
- (minor caveats but) No!
- No way to extract a long witness from a short proof. Need assumption (RO, “knowledge assumption”) that guarantees adversary “knows” a long string given a short commitment.
- Can (ZK-)SNARGs for NP be built based on falsifiable assumptions?
- It’s complicated. (We don’t know)
- Significant barriers [Gentry-Wichs ‘11]
- The community is still trying to understand this.
- Prove security assuming that some concrete algorithmic task is infeasible:
- SNARGs for limited computations from falsifiable assumptions (LWE)
- Two tools/techniques
- Correlation-intractable hash functions [CCHLRRW19,PS19,HLR21]
- Used to instantiate Fiat-Shamir without random oracles, for “nice enough” interactive protocols
- Somewhere extractable commitments [HW15]
- Used to make a “nice enough” interactive protocol
- Special variant of the typical IOP-based approach.
- Correlation-intractable hash functions [CCHLRRW19,PS19,HLR21]
- Two tools/techniques
- Correlation Intractability
- Function
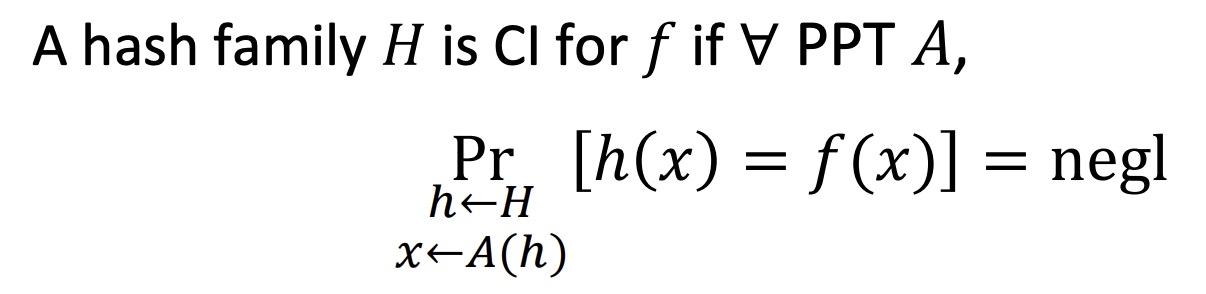
- Binary relations
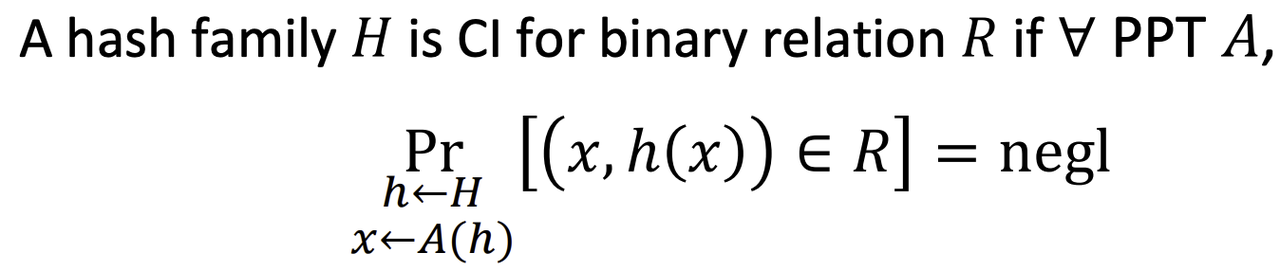
- Weren’t these impossible to build?
- Restrict to fixed input length (necessary)
- Restrict to fixed running time on f (unclear if necessary)
- CI Construction
- A simple construction [CLW18] using Fully Homomorphic Encryption (FHE)
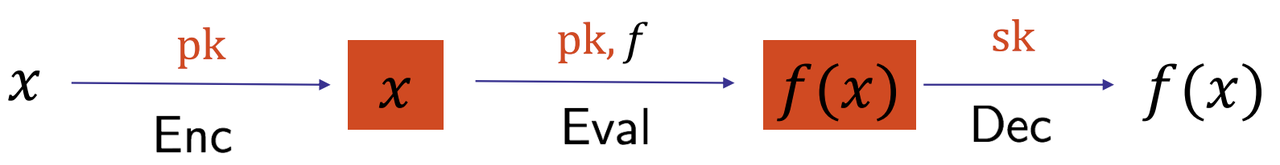

- A simple construction [CLW18] using Fully Homomorphic Encryption (FHE)
- Security Analysis

- Correlation Intractability: what we know

- Function