zkDT (CCS’20) Paper Reading
Zhang, Jiaheng, et al. “Zero knowledge proofs for decision tree predictions and accuracy.” Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security. 2020.
- Abstract
- In this paper, we initiate the study of zero knowledge machine learning and propose protocols for zero knowledge decision tree predictions and accuracy tests.
- Introduction
- Newly developed machine learning models are claimed to achieve high accuracy, yet it is challenging to reproduce the results and validate these claims in many cases. In addition, even if a high quality model exists, it may not be used consistently in real-world products.
- In this paper, we initiate the study of zero knowledge machine learning predictions and accuracy, and propose several efficient schemes for zero knowledge decision trees. We also extend our techniques with minimal changes to support variants of decision trees, including regression, multivariate decision trees and random forests.
- Our Zero-knowledge Argument Backend
- In our construction and implementation, we aim to optimize for fast prover time and to scale to large decision trees. Therefore, after careful comparisons among all existing ZKP systems, we choose the scheme named Aurora proposed in [10] as the ZKP backend in our zero knowledge decision tree construction.
- Aurora has no trusted setup. Its security is proven in the random oracle model, and is plausibly post-quantum secure. It can be made non-interactive using Fiat-Shamir in the random oracle model.
- Zero-knowledge Decision Tree
- Decision Tree
- In a decision tree T , each intermediate node contains an attribute, each branch represents a decision and each leaf node denotes an outcome (categorical or continues value). More formally, each internal node v has an associated attribute indexv.att from the set [d] of d attributes, a threshold v.thr and two children v.left and v.right. Each leaf node u stores the classification result u.class. Each data sample is represented as a size-d vector a of values corresponding to each attribute.
- It starts from the root of T . For each node of v in T , it compares a[v.att] with v.thr, and moves to v.left if a[v.att] < v.thr, and v.right otherwise.

- In our scheme, we only consider proving predictions given the pretrained decision tree, and the training process is out of scope.
- Decision Tree
- Zero Knowledge Decision Tree Prediction

- Authenticated Decision Tree
- To validate the prediction for a data sample, the proof includes the prediction path from the root to the leaf node that outputs the prediction result. In addition, the proof also includes the hashes of the siblings of the nodes along the prediction path. With the proof, the verifier can recompute the root hash and compare it with the commitment. In this way, to prove the validity of a prediction, the verification only computes O(h) hashes.
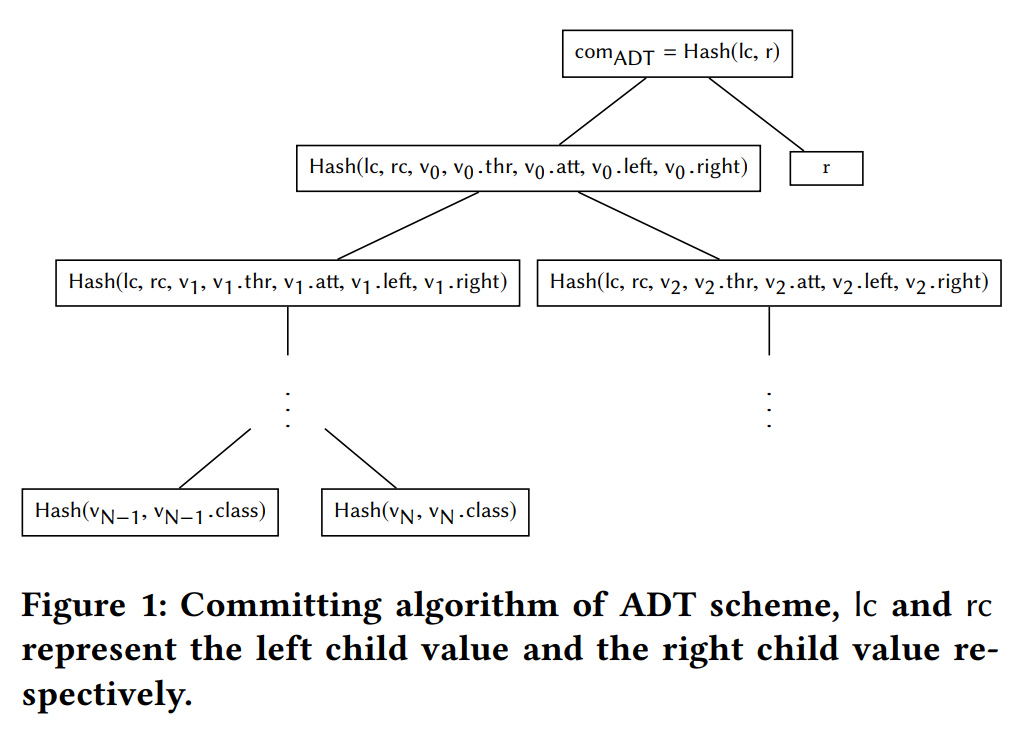
- Note that in order to prove the zero knowledge property of the scheme later, the commitment has to be randomized and we add a random point r to the root of the decision tree and use the hash of the root concatenated with r as the final commitment.

- To validate the prediction for a data sample, the proof includes the prediction path from the root to the leaf node that outputs the prediction result. In addition, the proof also includes the hashes of the siblings of the nodes along the prediction path. With the proof, the verifier can recompute the root hash and compare it with the commitment. In this way, to prove the validity of a prediction, the verification only computes O(h) hashes.
- Proving the validity of the prediction
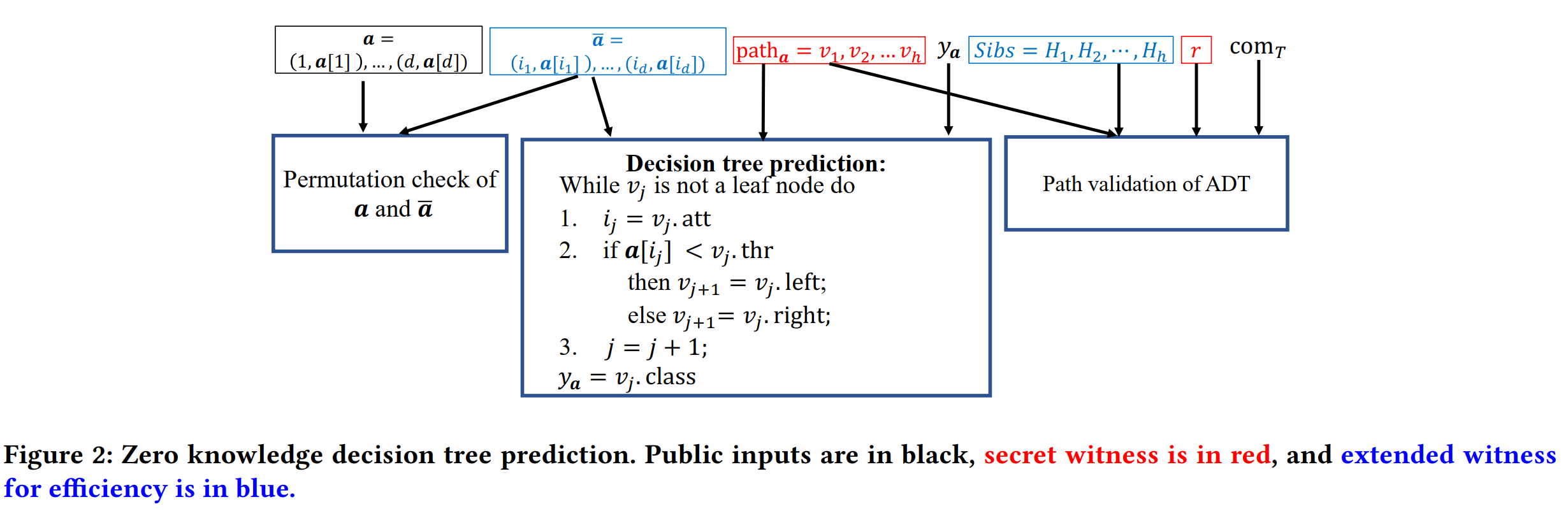
- Decision tree prediction.

- Permutation test.

- Path validation.

- Decision tree prediction.
- Zero Knowledge Decision Tree Accuracy
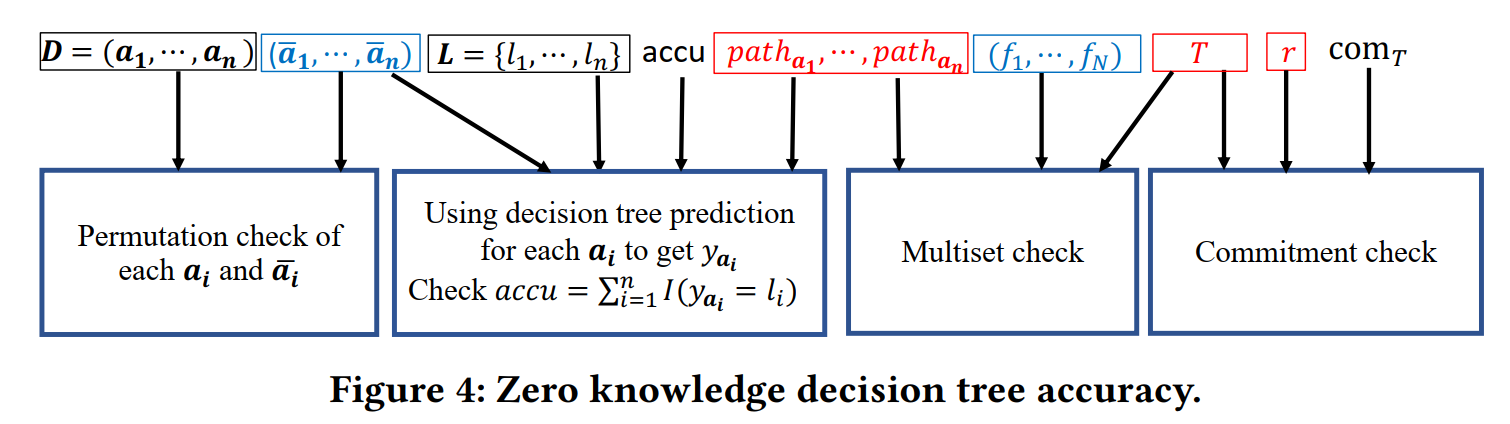

- Checking Multiset
- Instead of validating each prediction path one by one, the idea is to validate all N nodes of the decision tree in one shot. Then the circuit checks that the nodes of each prediction path are drawn from these N nodes of the decision tree and they form a path with the correct parentchildren relationships.

- Instead of validating each prediction path one by one, the idea is to validate all N nodes of the decision tree in one shot. Then the circuit checks that the nodes of each prediction path are drawn from these N nodes of the decision tree and they form a path with the correct parentchildren relationships.
- Validating Decision Tree
- Using ADT, we can validate it by reconstructing the decision tree in the circuit $2^h$ hashes. However, in practice, we notice that most decision trees are not balanced.
- We first replace the commitment by a hash of all N nodes concatenated by a random value r, instead of the root of the ADT. In addition, each node contains a unique id(id) in [N], the id of its parent (pid), left child (lid), right child (rid) and its depth (depth) in [h] (the id is 0 means the parent or the child is empty). To verify that all N nodes of T1,T2, · · · ,TN form a binary decision tree, it suffices to check the following conditions:


- There is no guarantee on other nodes of the N nodes provided by the prover, but they are not used in the prediction paths anyway, which is good enough for our purposes.
- Checking Multiset