Maximum Flow Problem

Maximum Flow Problem
- Description
- Naive Algorithm
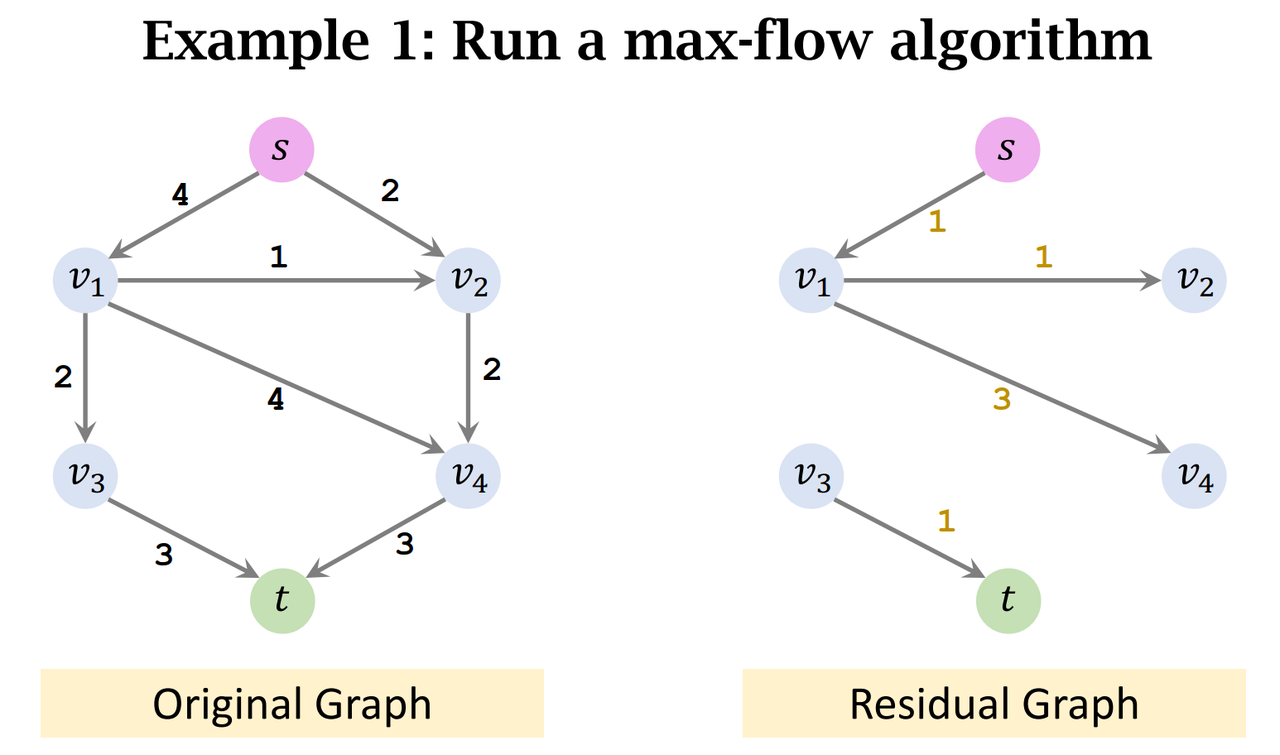
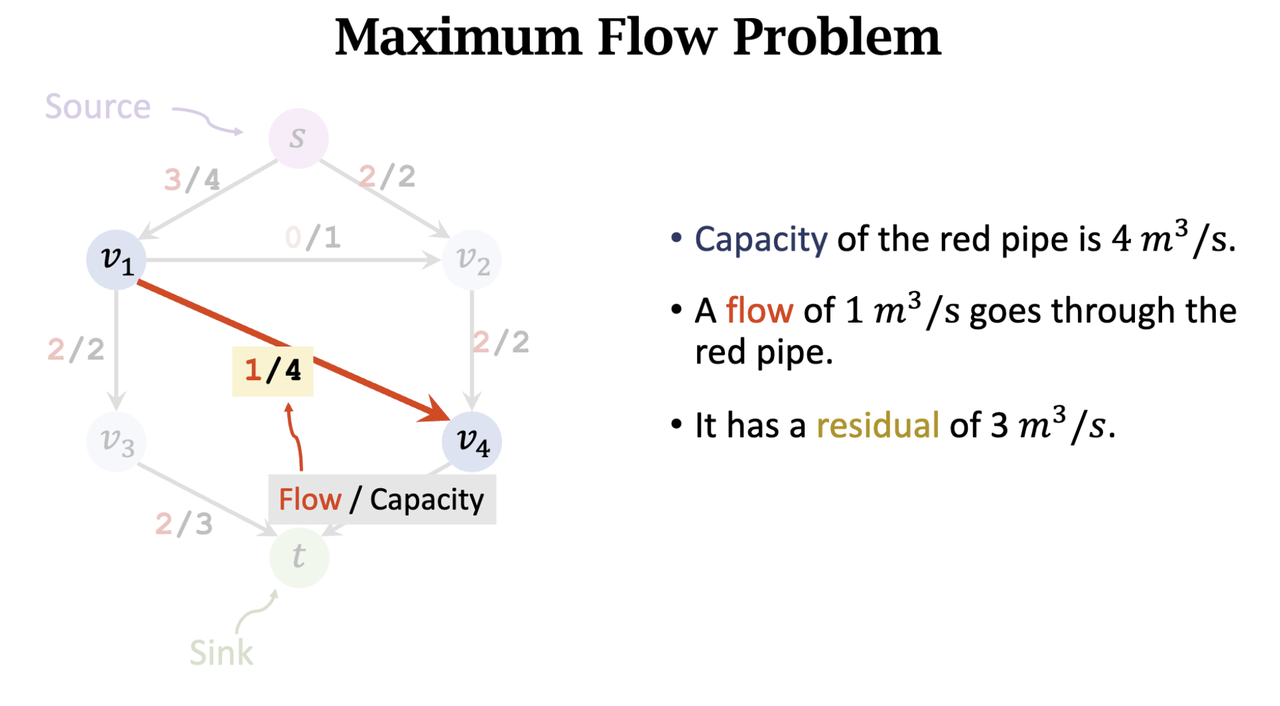
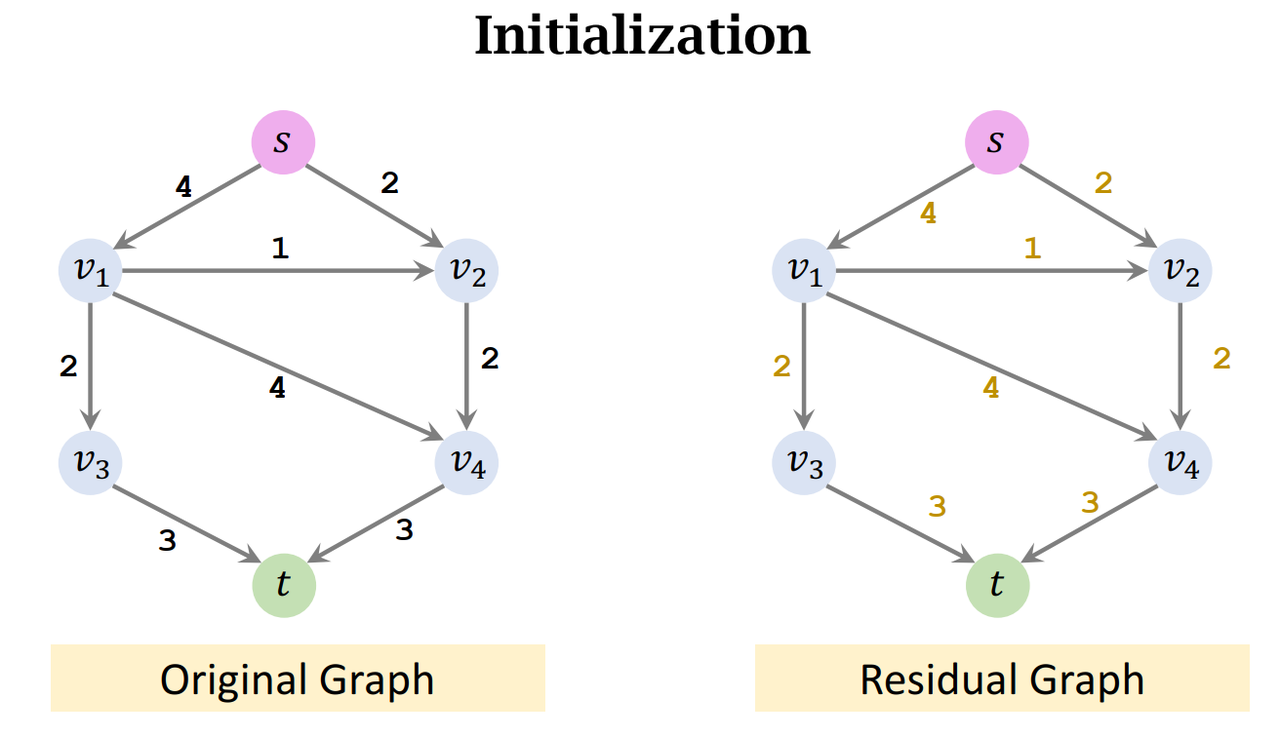
  - Residual = Capacity - Flow
  - Left: Original Graph
  - Right: Residual Graph
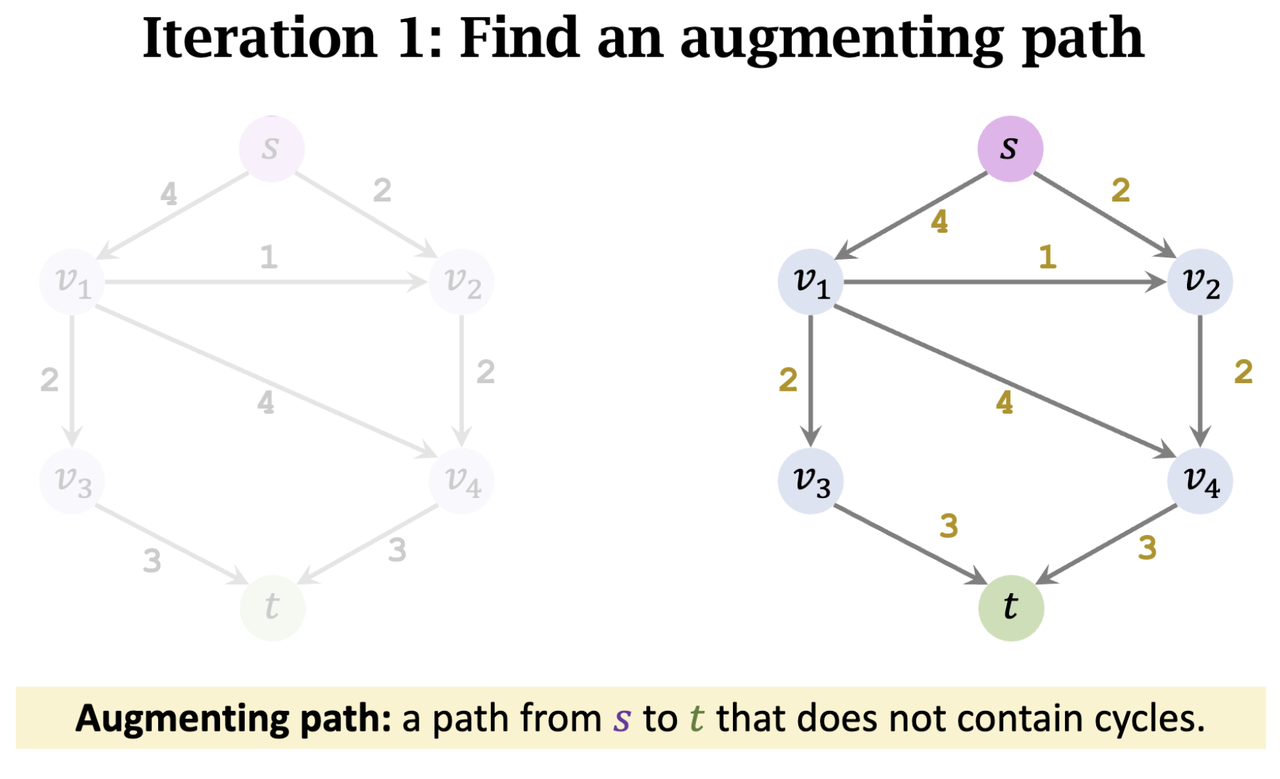
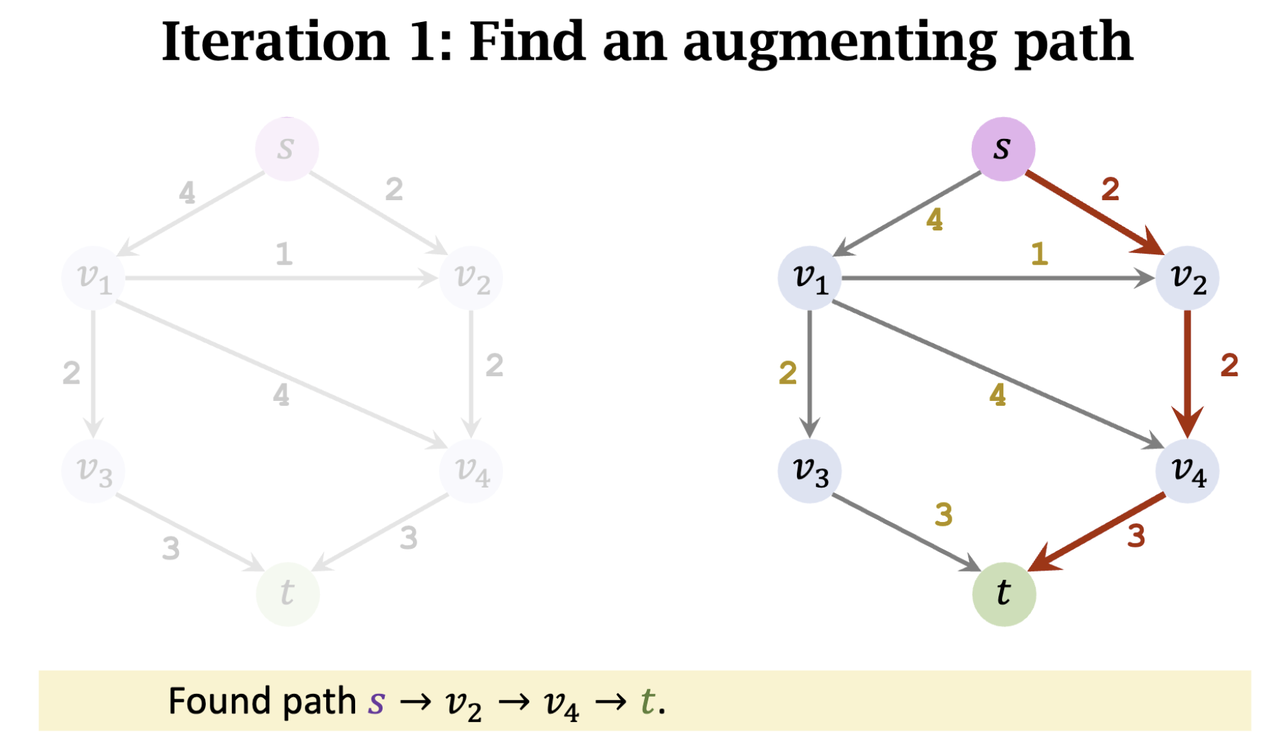
  - Bottleneck capacity = 2
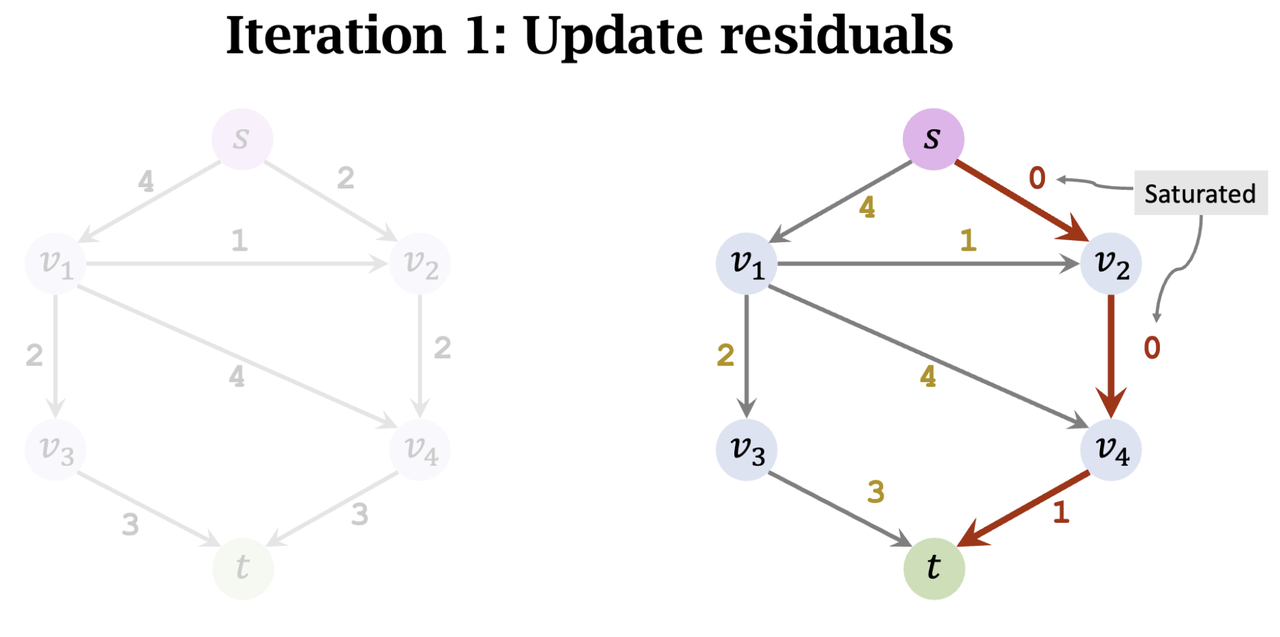
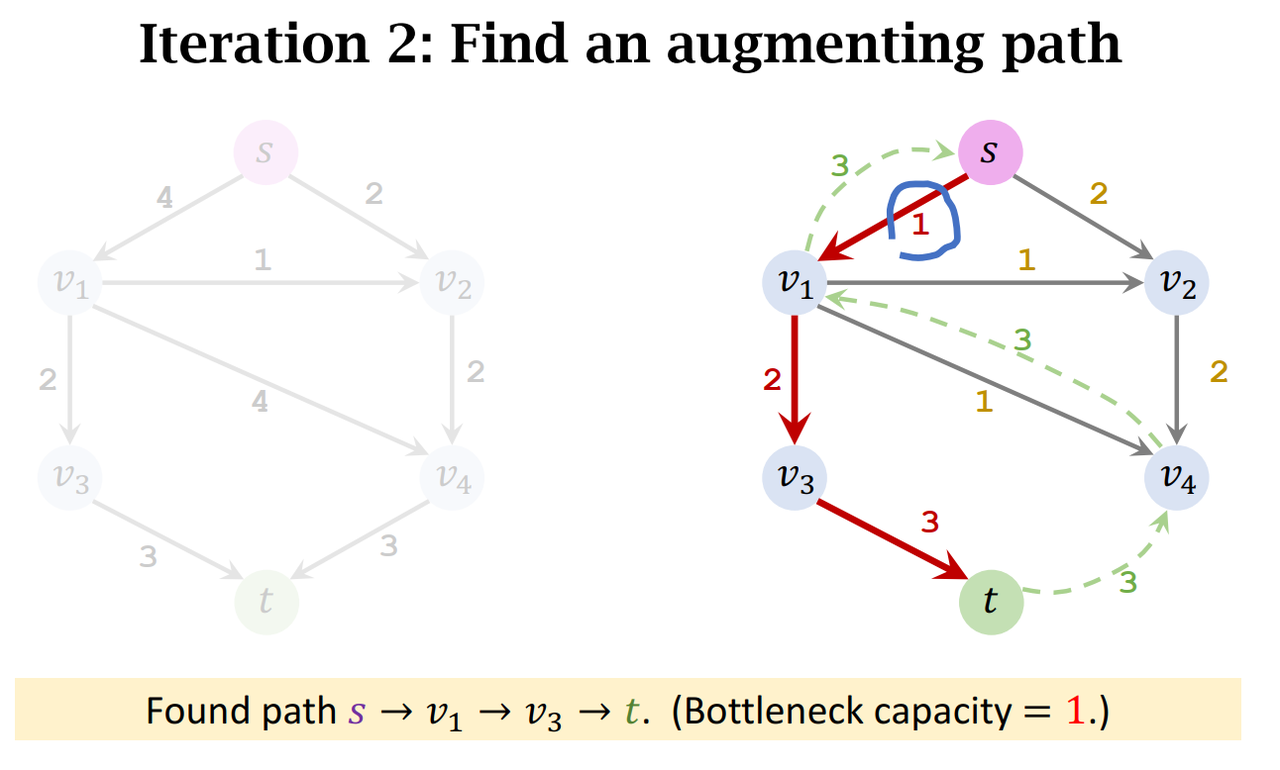
  - Iteration 2:
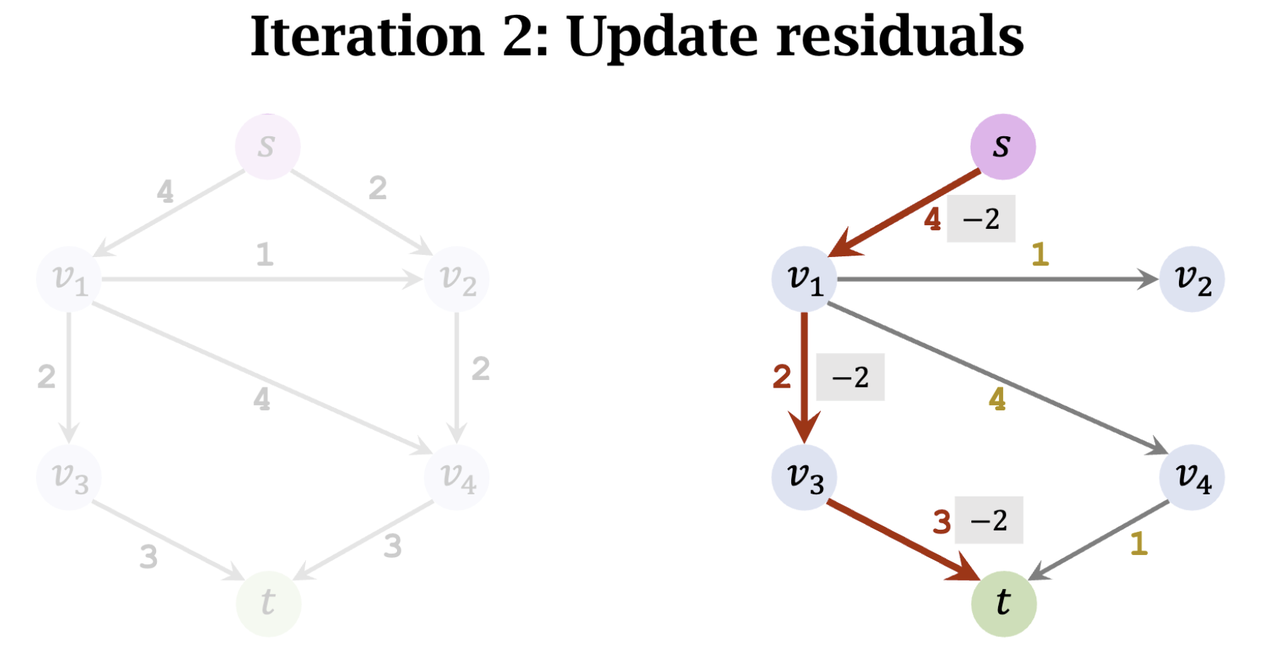
    - Find an augmenting path: s -> v_1 -> v_3 -> t
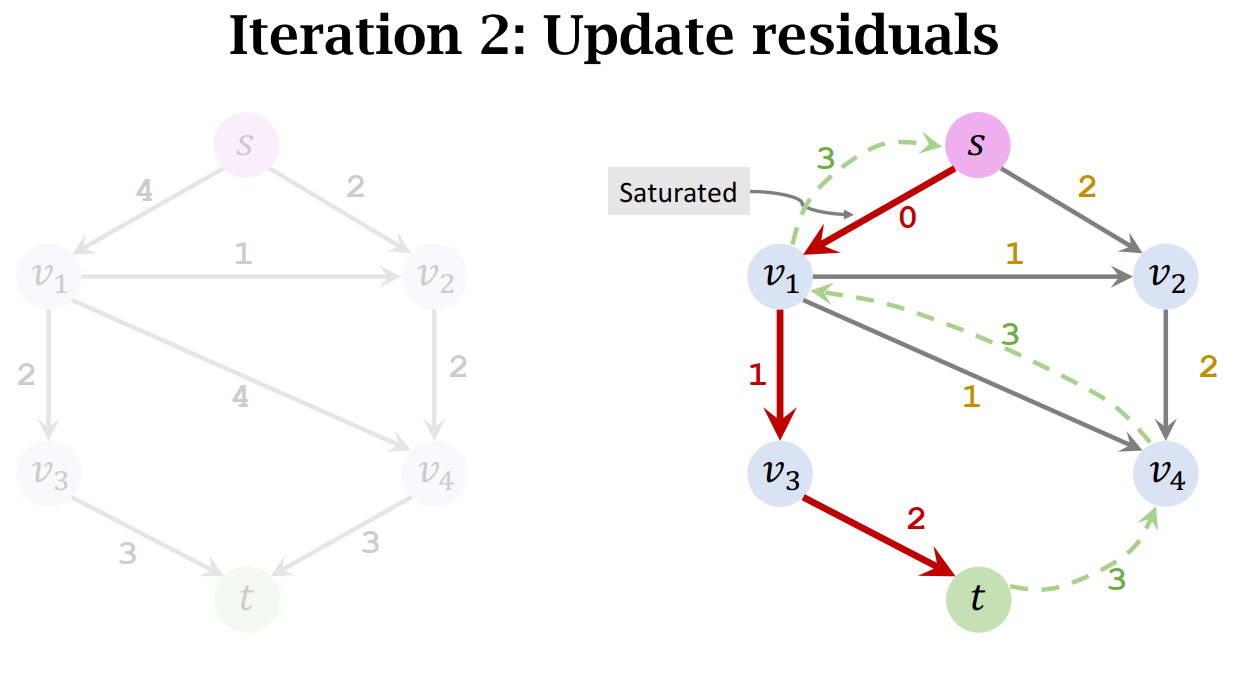
    - Update residuals

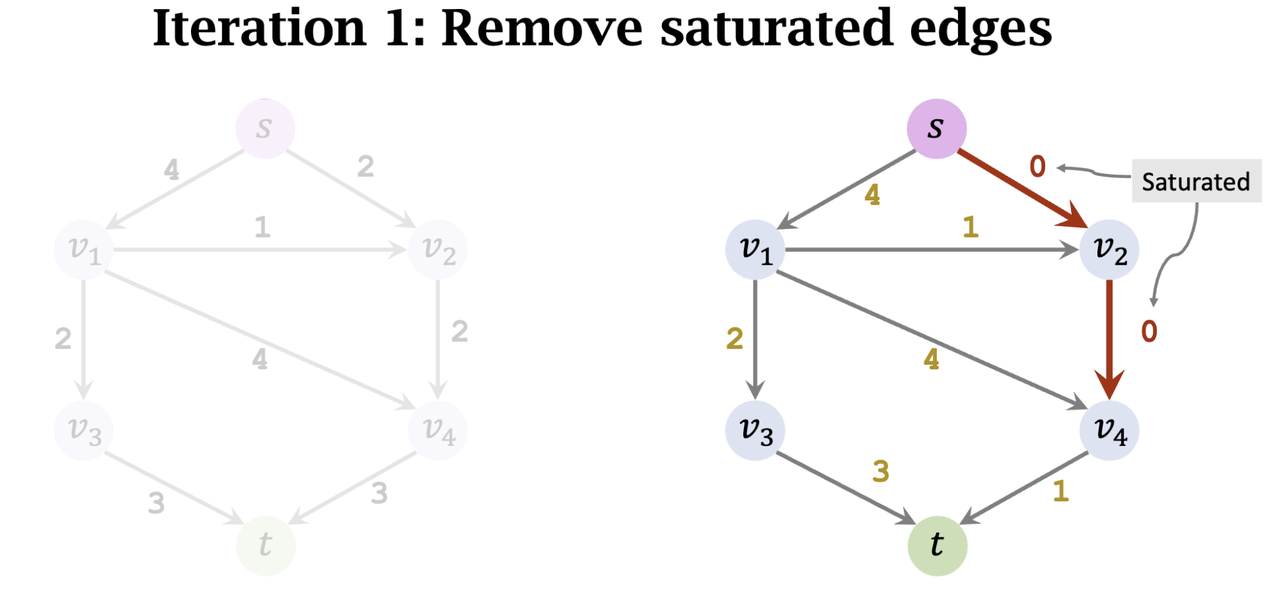
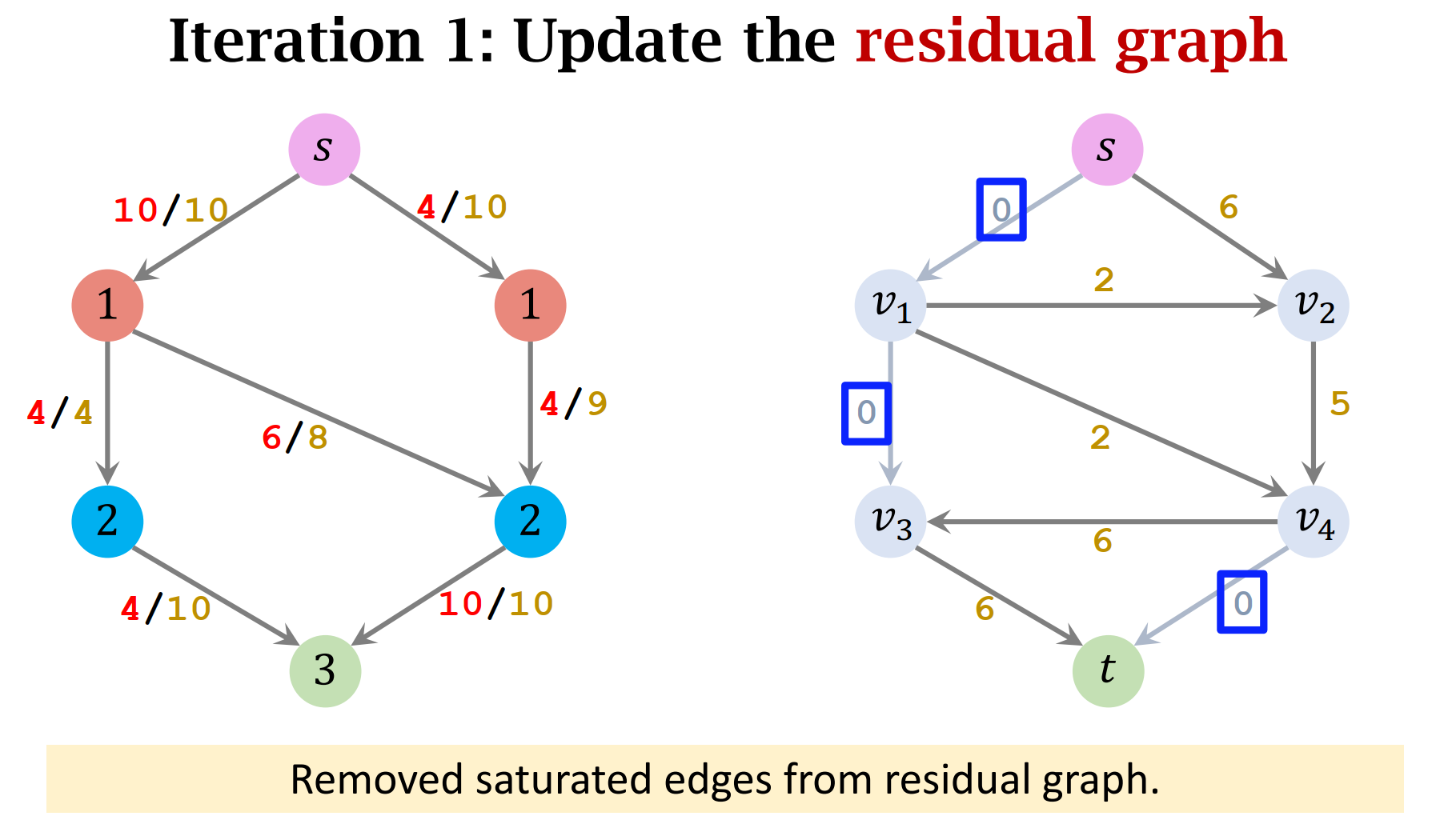
- Remove saturated edge
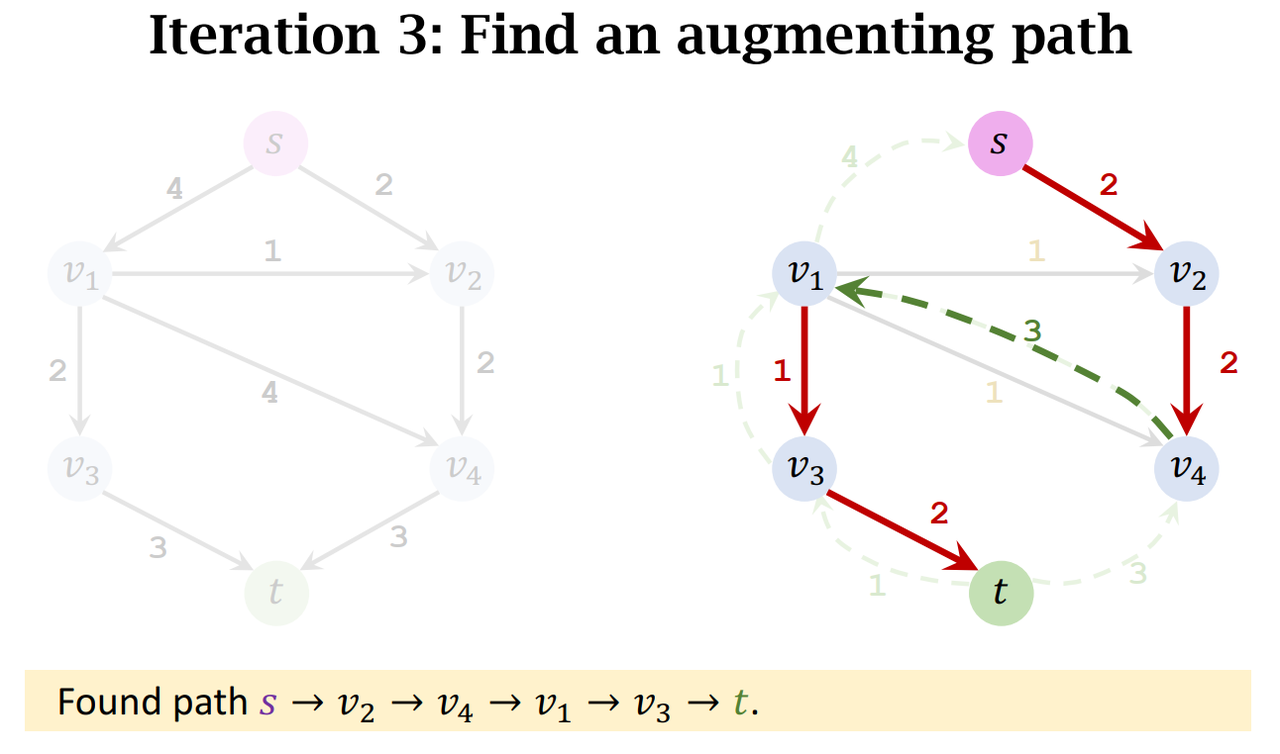
- Iteration 3:
- Find an augmenting path: s -> v_1 -> v_4 -> t
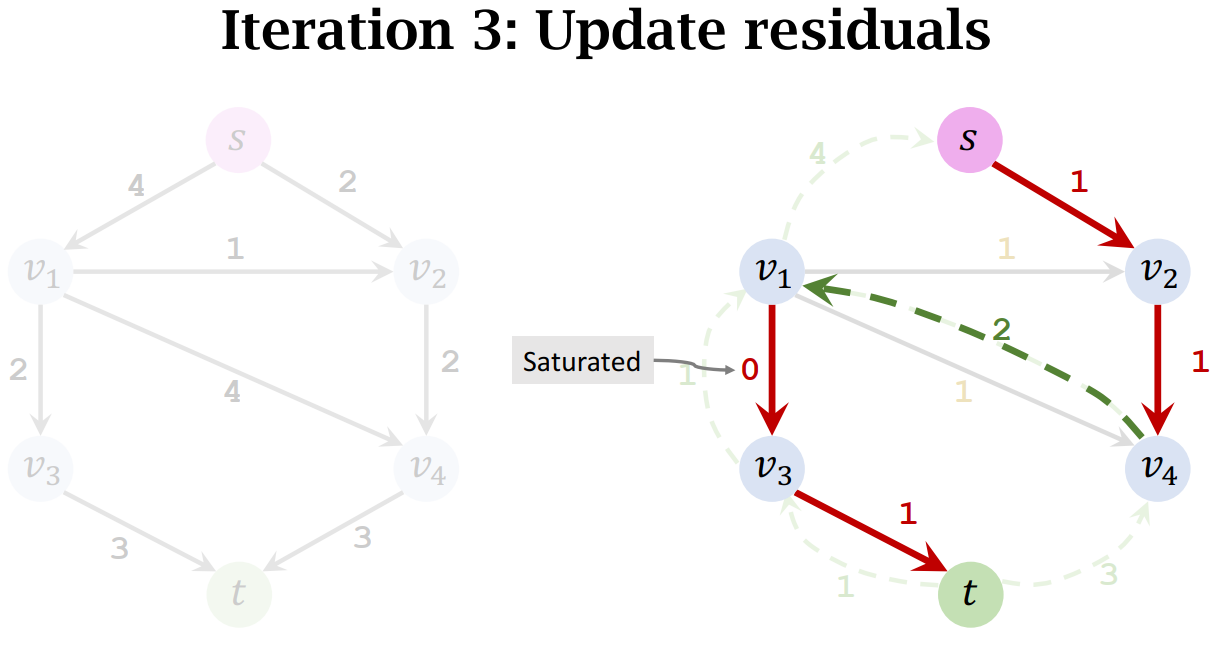
- Update residuals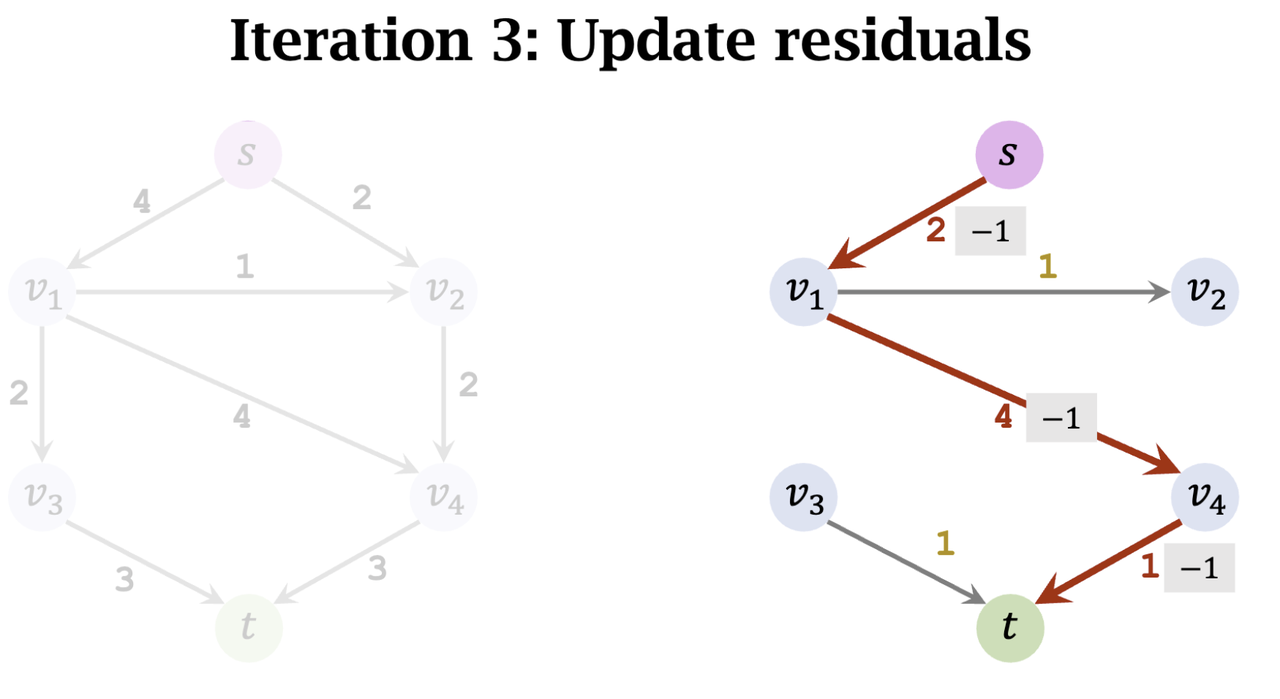

- Remove saturated edge
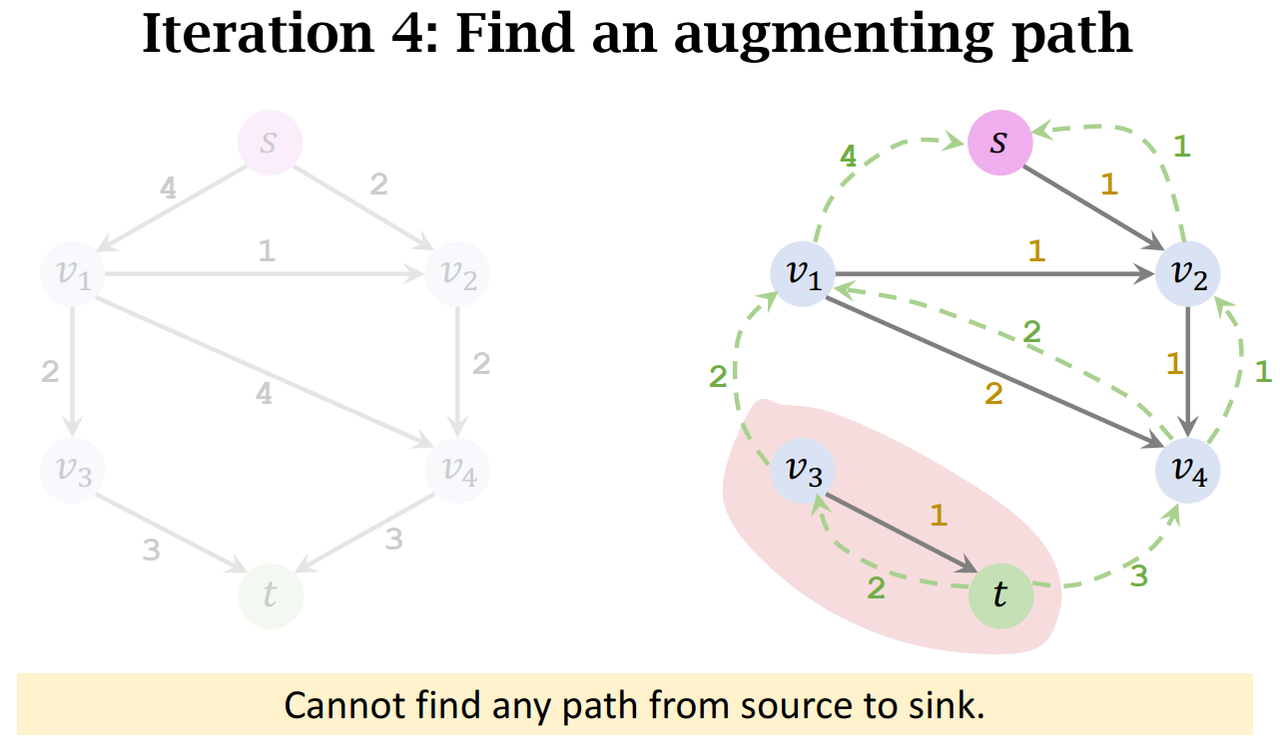
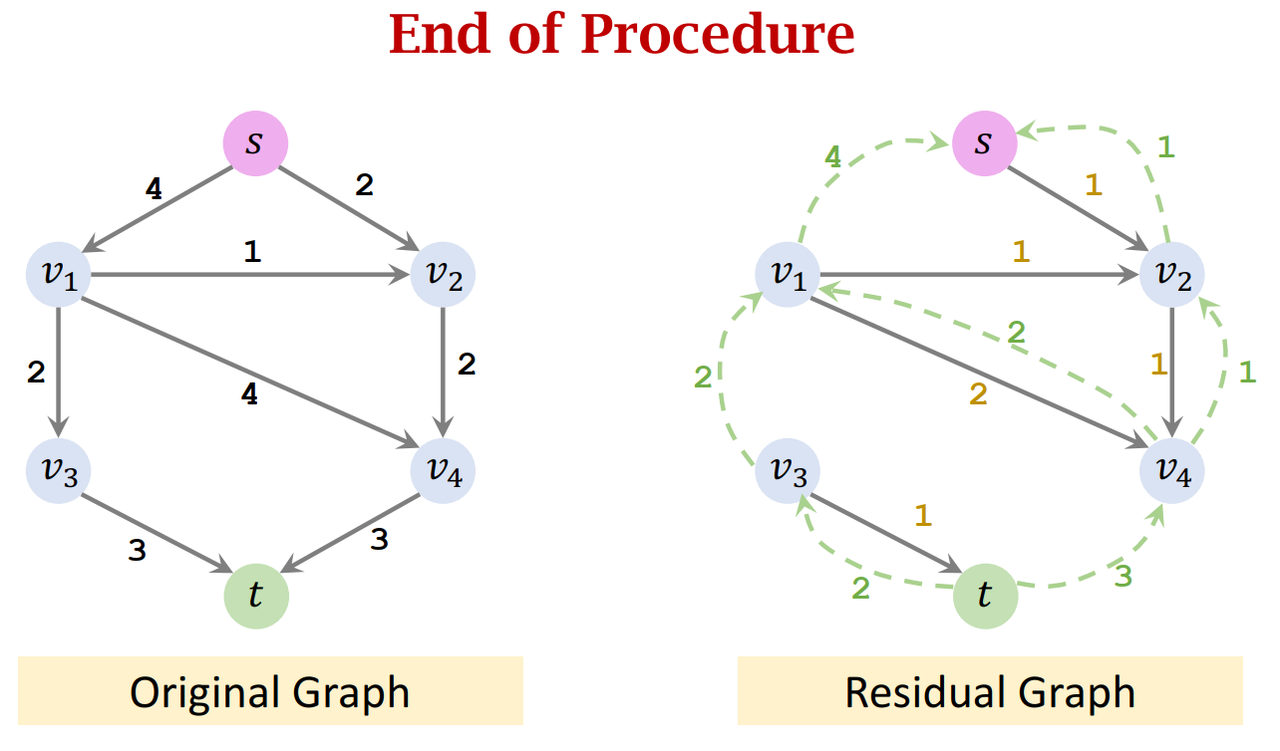
- Iteration 4:
- Cannot find an augmenting path: end of procedure
- Summay
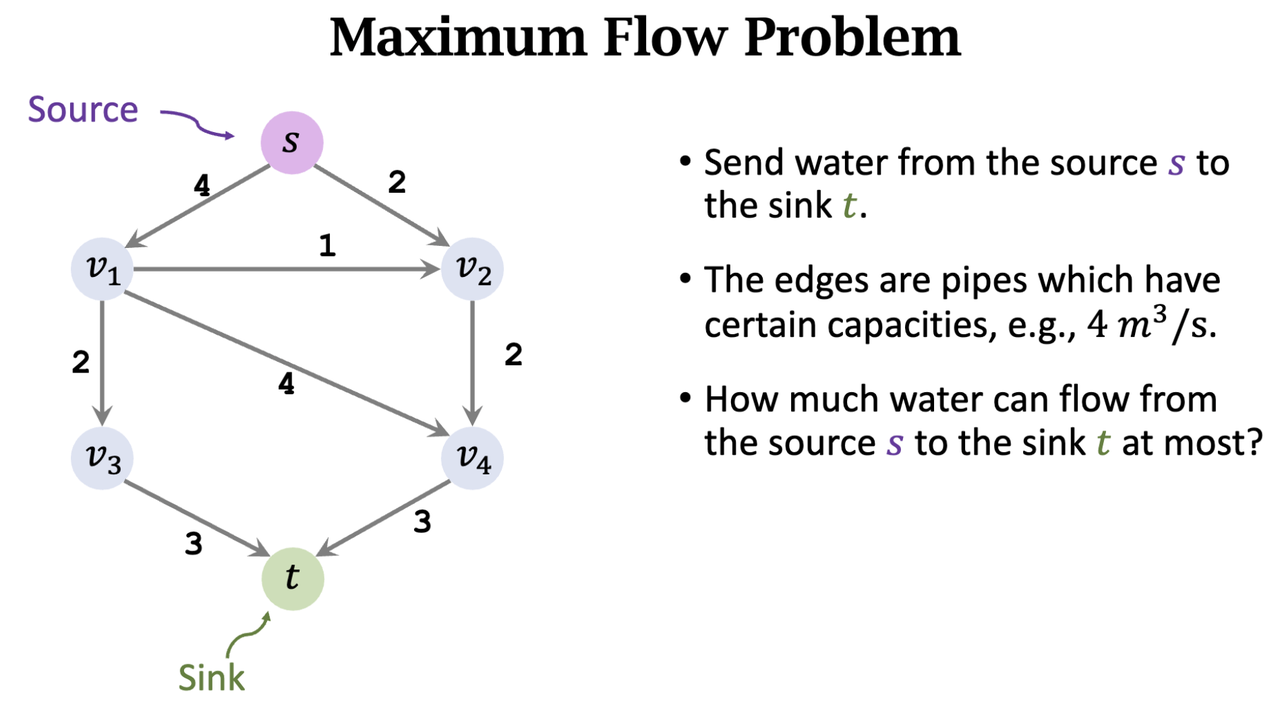
- Inputs: a weighted directed graph, the source 𝑠, and the sink 𝑡.
- Goal: Send as much water as possible from 𝑠 to 𝑡
- Constraints:
- Each edge has a weight (i.e., the capacity of the pipe).
- The flow must not exceed capacity.
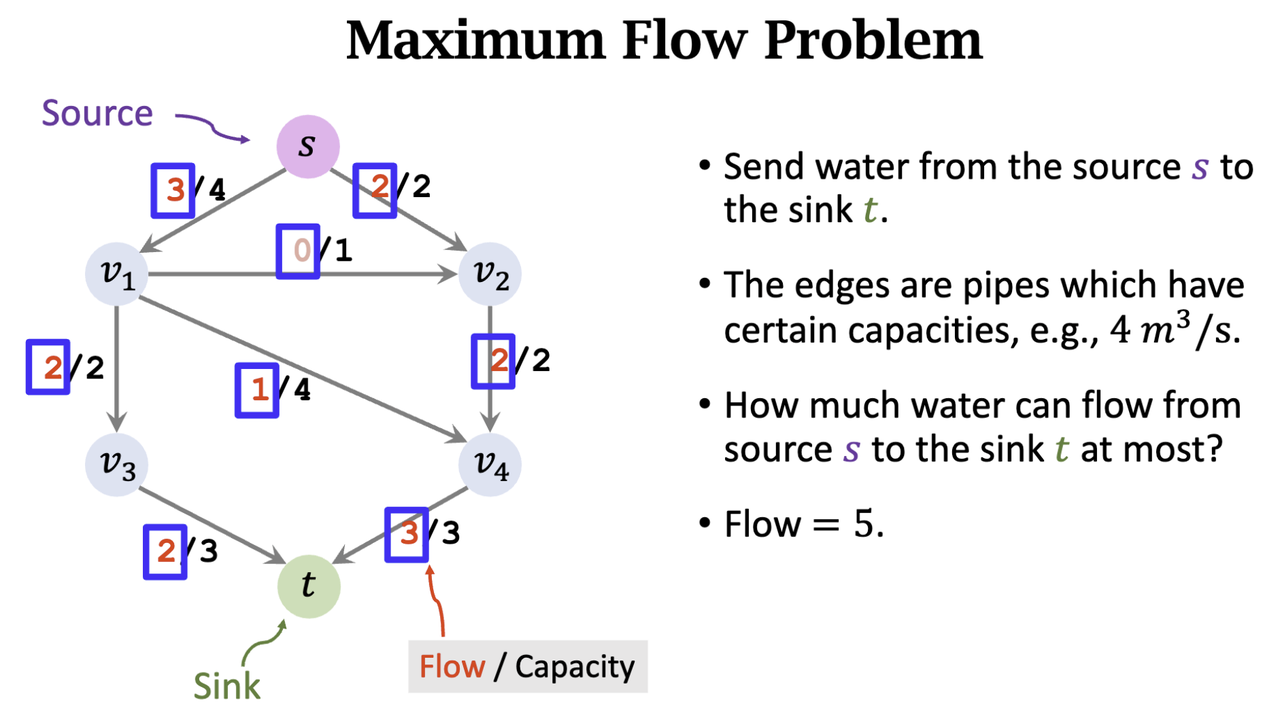
- naïve algorithm
- Build a residual graph; initialize the residuals to the capacity.
- While augmenting path can be found:
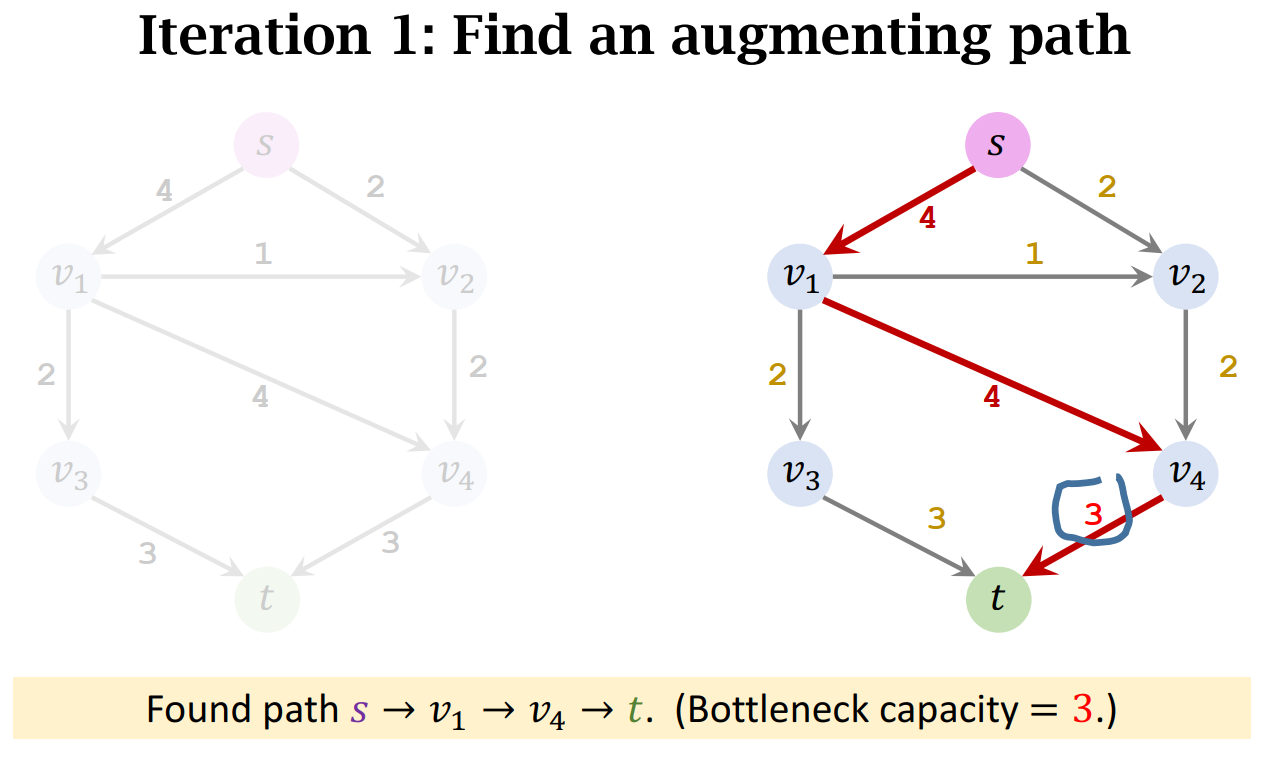
- a. Find an augmenting path (on the residual graph.)
- b. Find the bottleneck capacity 𝑥 in the augmenting path.
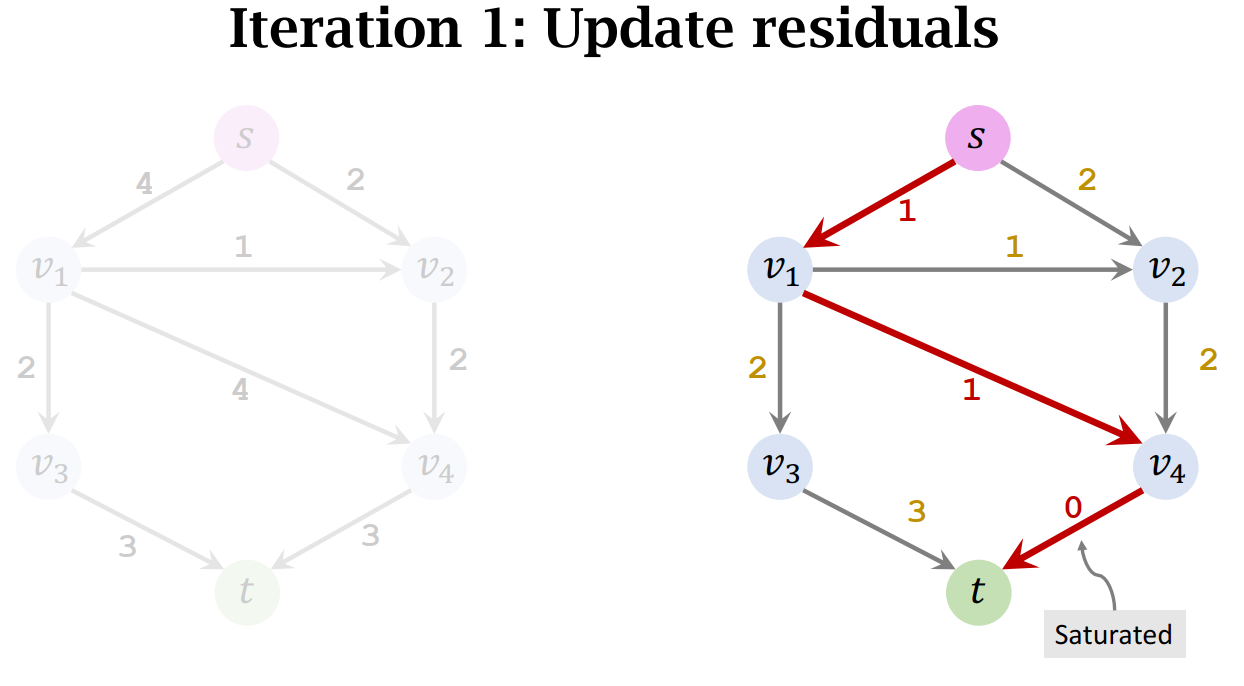
- c. Update the residuals. (residual ← residual − 𝑥.)
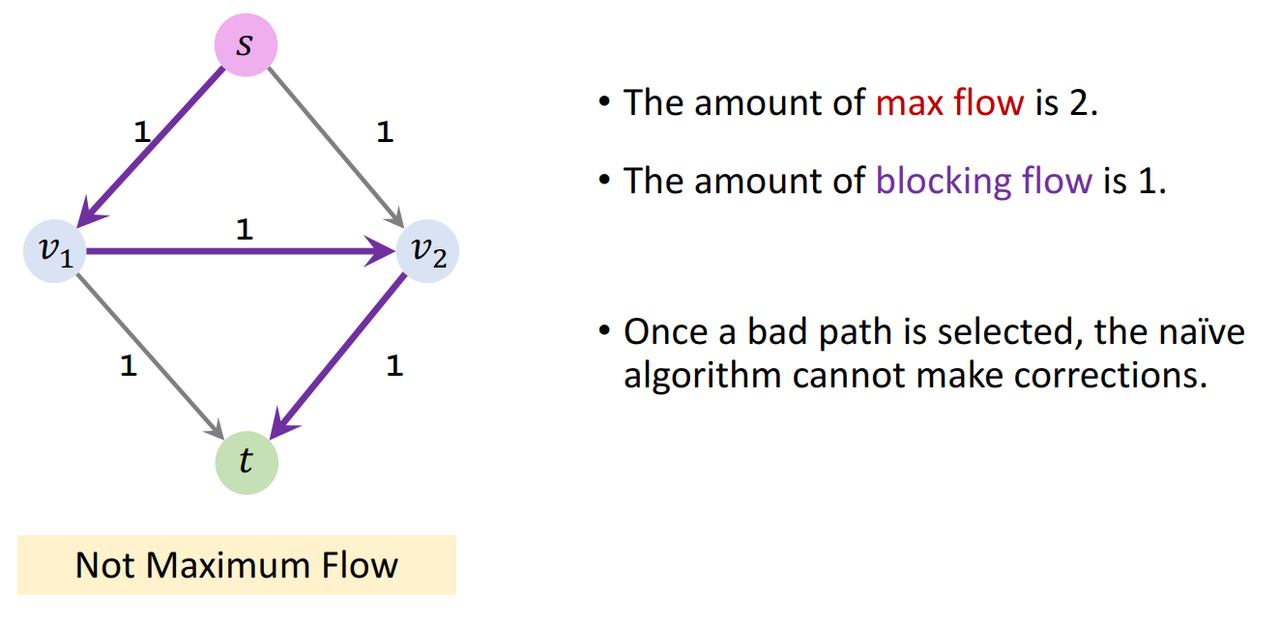
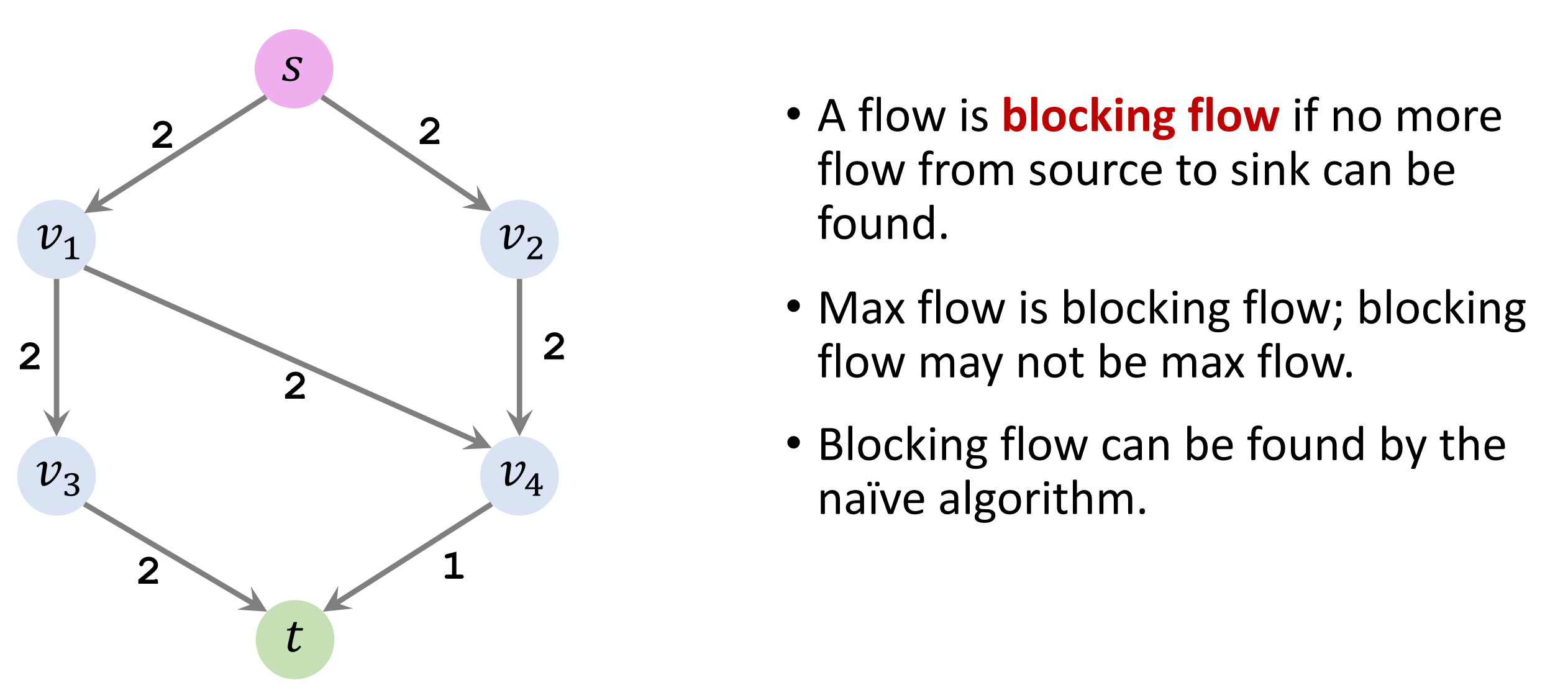
- The naïve algorithm can fail
- The naïve algorithm always finds the blocking flow.
- However, the outcome may not be the maximum flow.

Ford-Fulkerson Algorithm
- Problem with the naïve algorithm
- Procedure
- Worst-Case Time Complexity
- Summary
  - Ford-Fulkerson Algorithm
    - Build a residual graph; initialize the residuals to the capacities
    - While augmenting path can be found:
      - Find an augmenting path (on the residual graph.)
      - Find the bottleneck capacity 𝑥 on the augmenting path.
      - Update the residuals. (residual ← residual − 𝑥.)
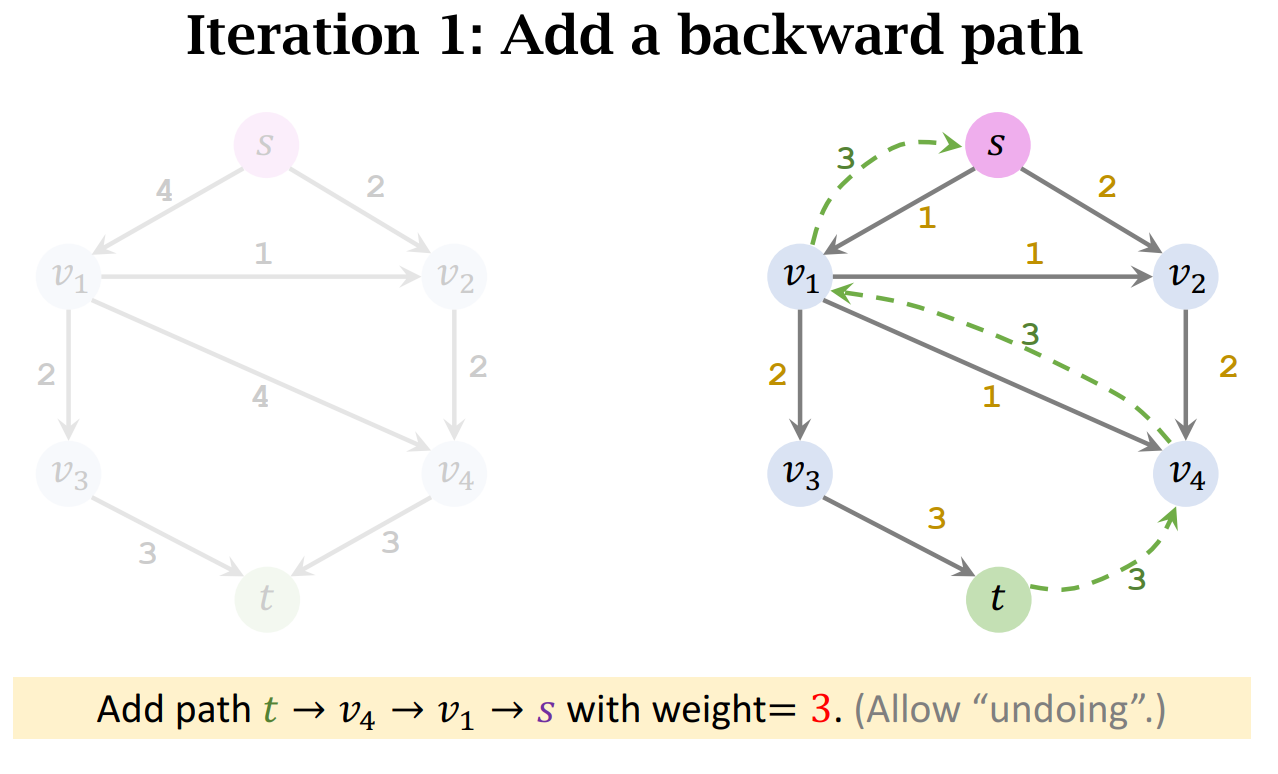
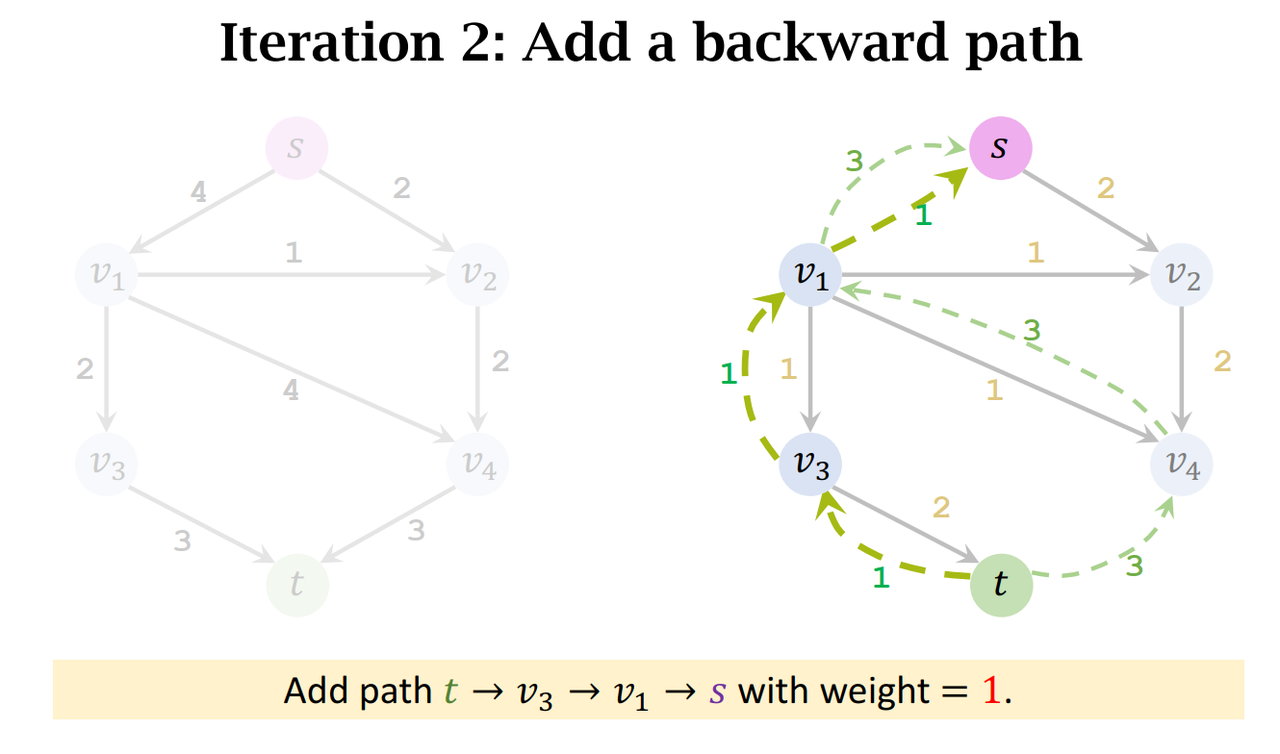
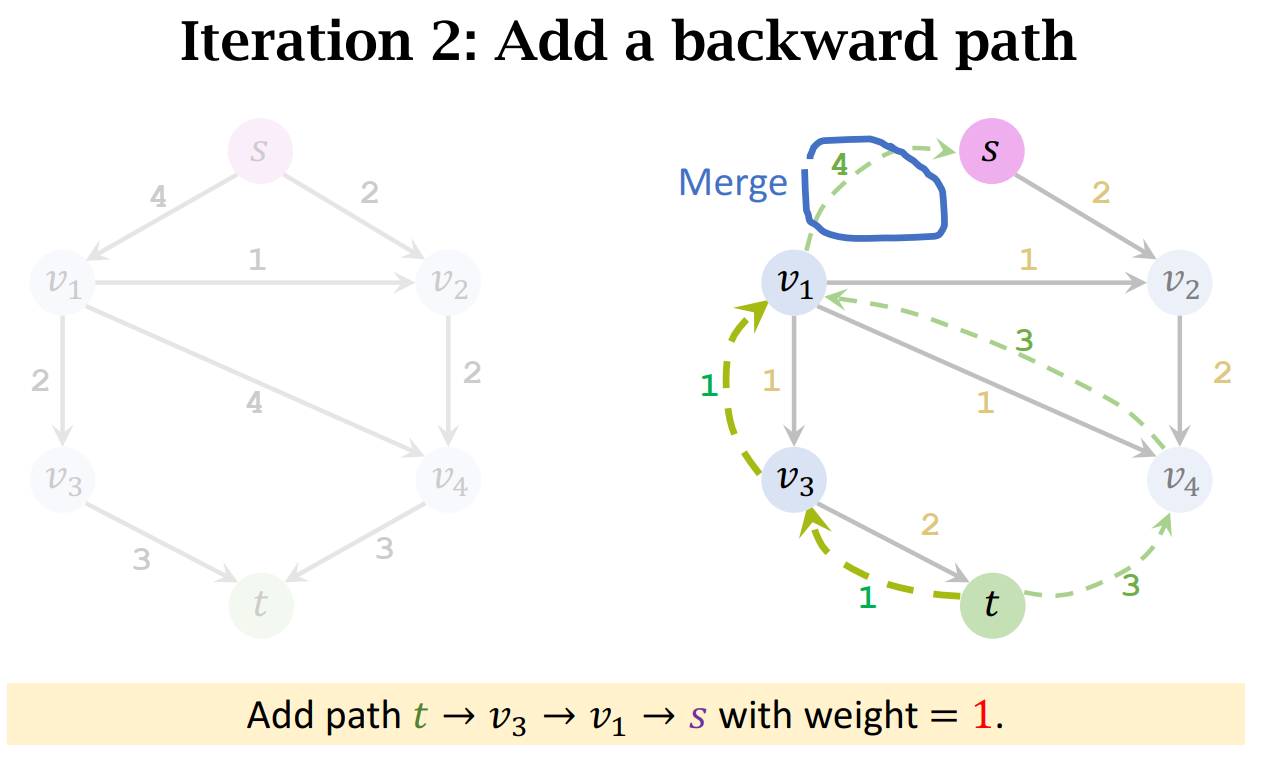
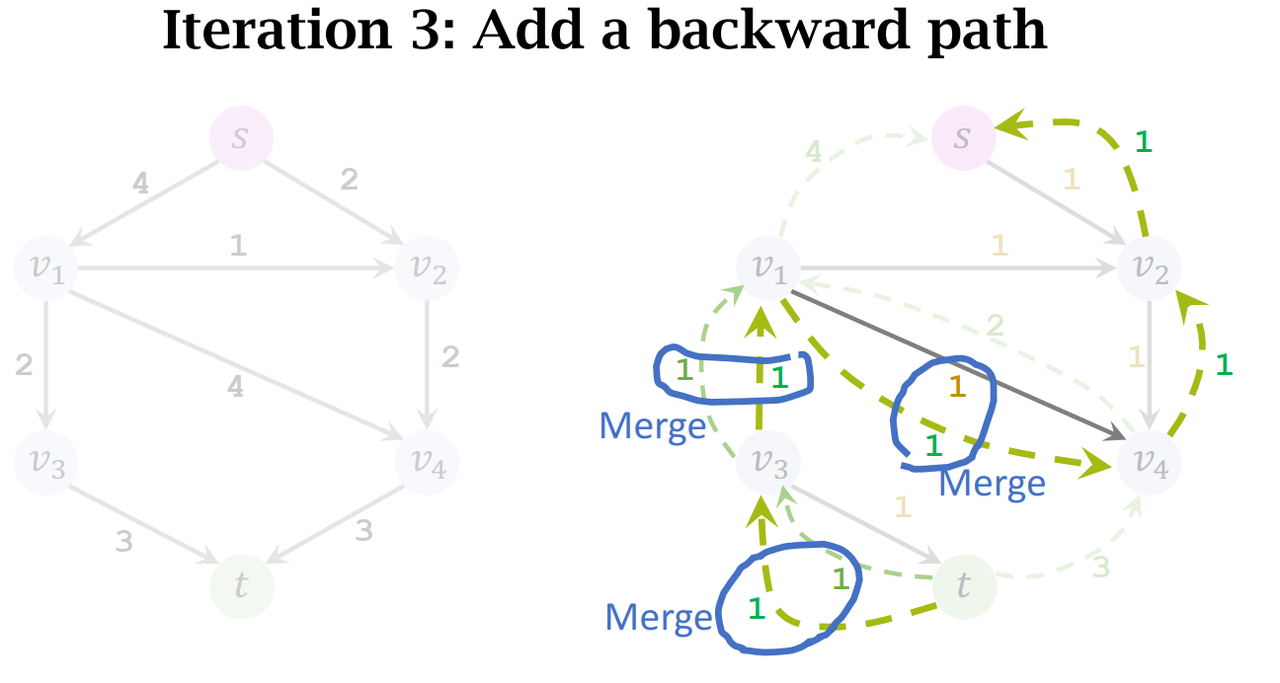
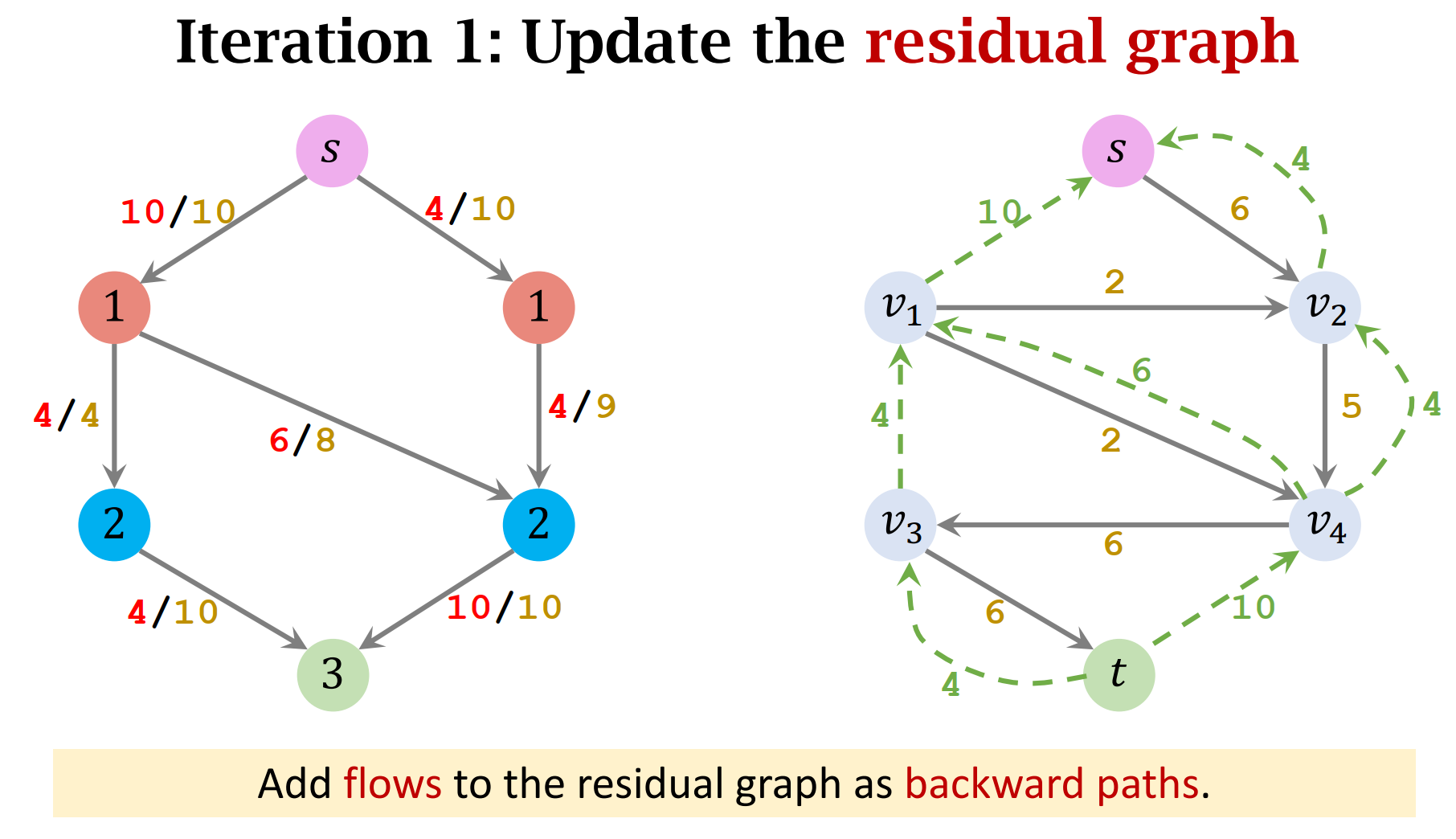
      - Add a backward path. (Along the path, all edges have weights of 𝑥.)
  - Time complexity: 𝑂(𝑓⋅𝑚). (𝑓 is the max flow; 𝑚 is #edges.)
Edmonds-Karp Algorithm
- Procedure
  - Build a residual graph; initialize the residuals to the capacities.
  - While augmenting path can be found:
    - Find the shortest augmenting path (on the residual graph.)
    - Find the bottleneck capacity 𝑥 on the augmenting path.
    - Update the residuals. (residual ← residual − 𝑥.)
    - Add a backward path. (Along the path, all edges have weights of 𝑥.)
- Note: Edmonds-Karp algorithm uses the shortest path from source to sink. (Apply weight 1 to all the edges of the residual graph.)
- Time complexity: $O(m^2 \cdot n)$ . (m is #edges; n is #vertices.)
Dinic’s Algorithm
- Time complexity: $O(m \cdot n^2)$ . (m is #edges; n is #vertices.)
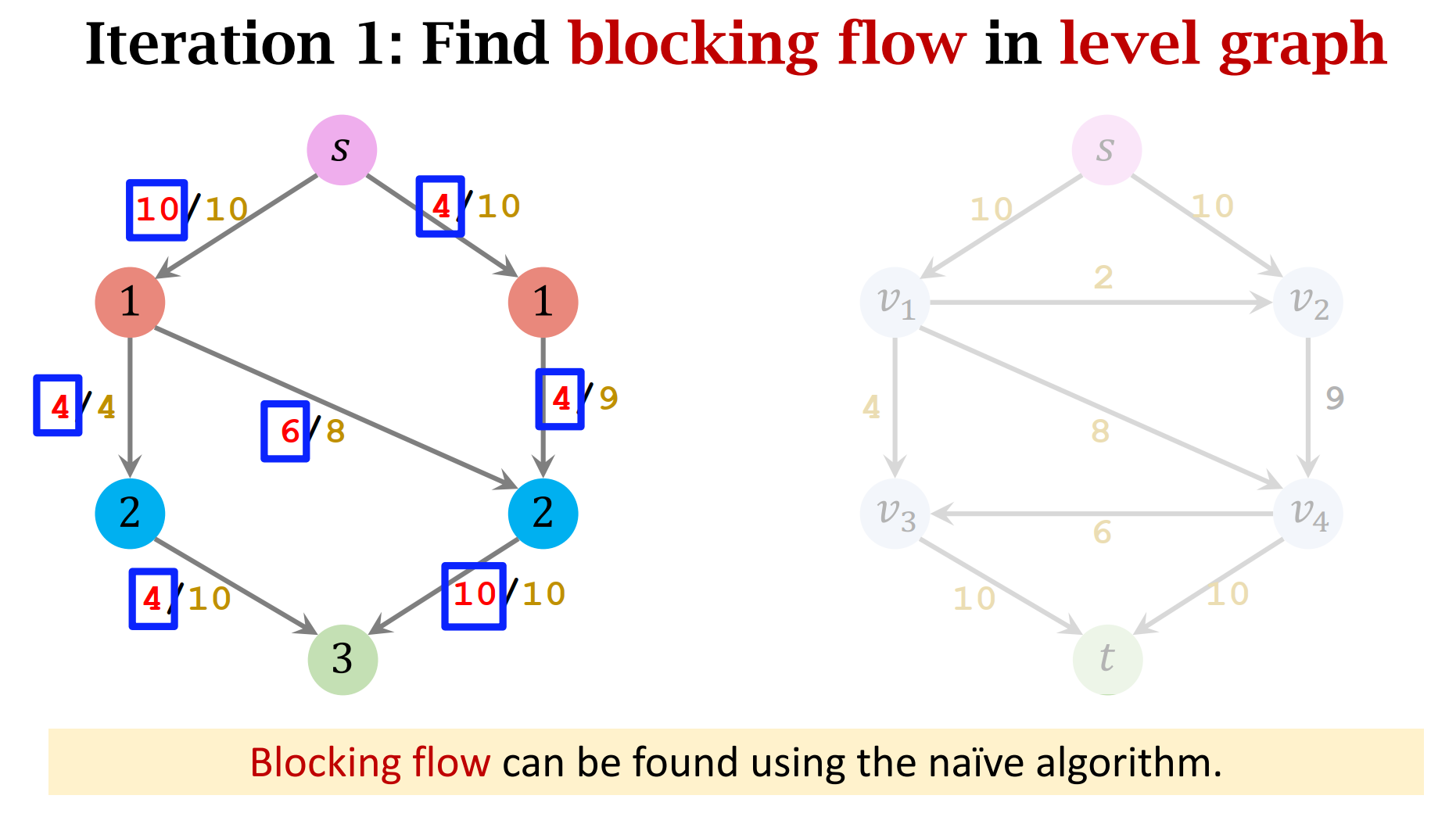
- Key Concept: Blocking Flow
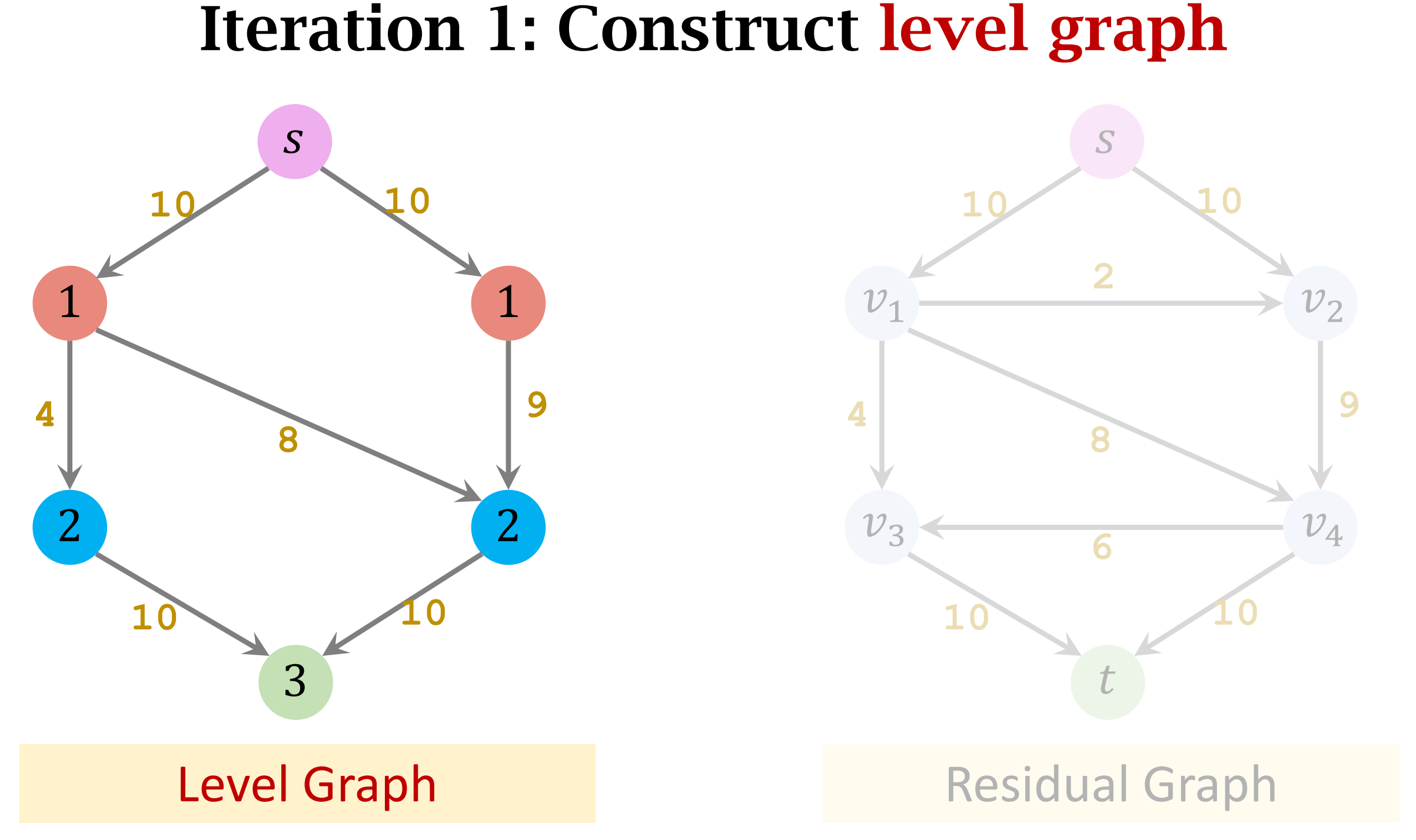
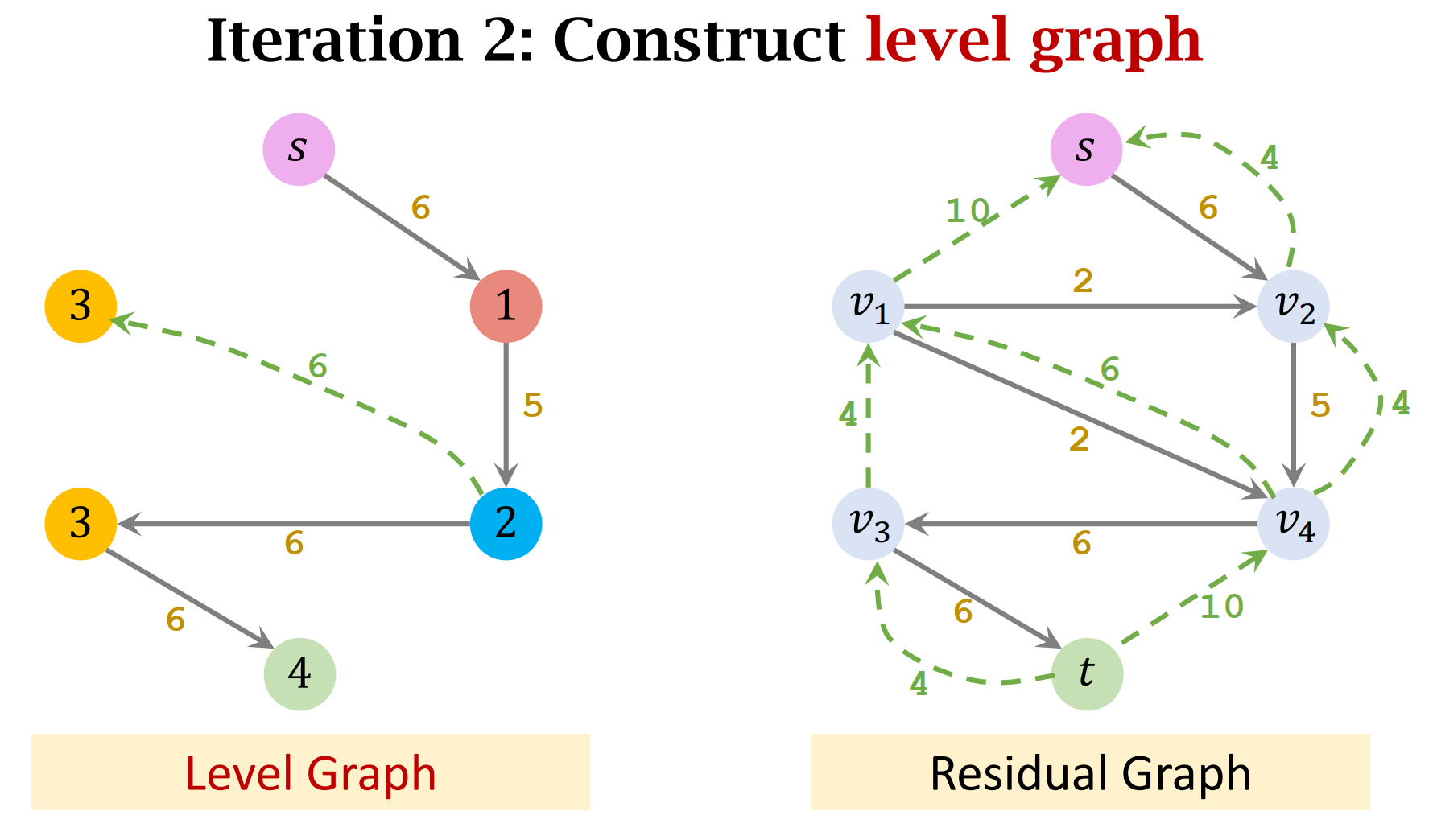
- Key Concept: Level Graph
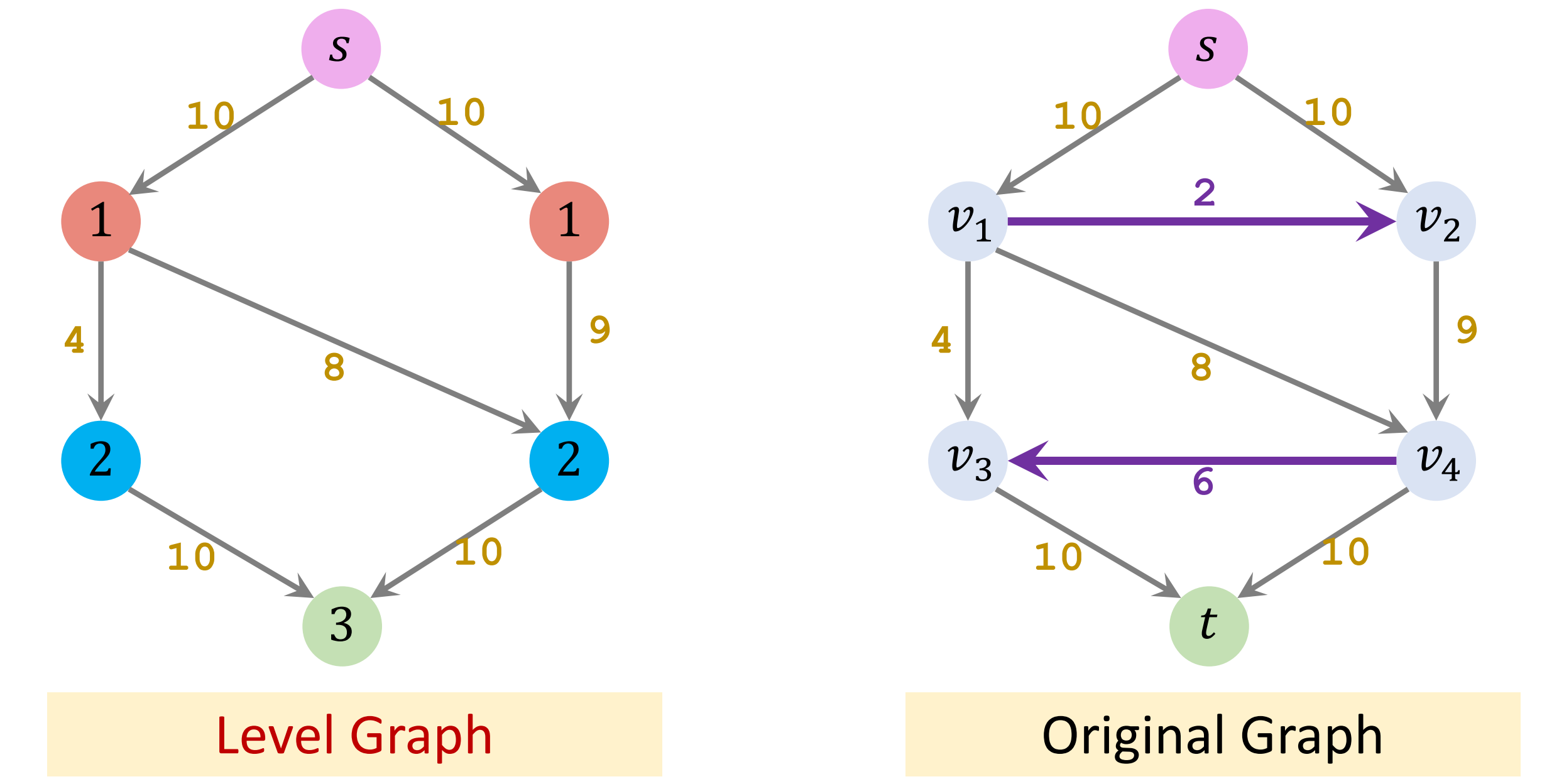
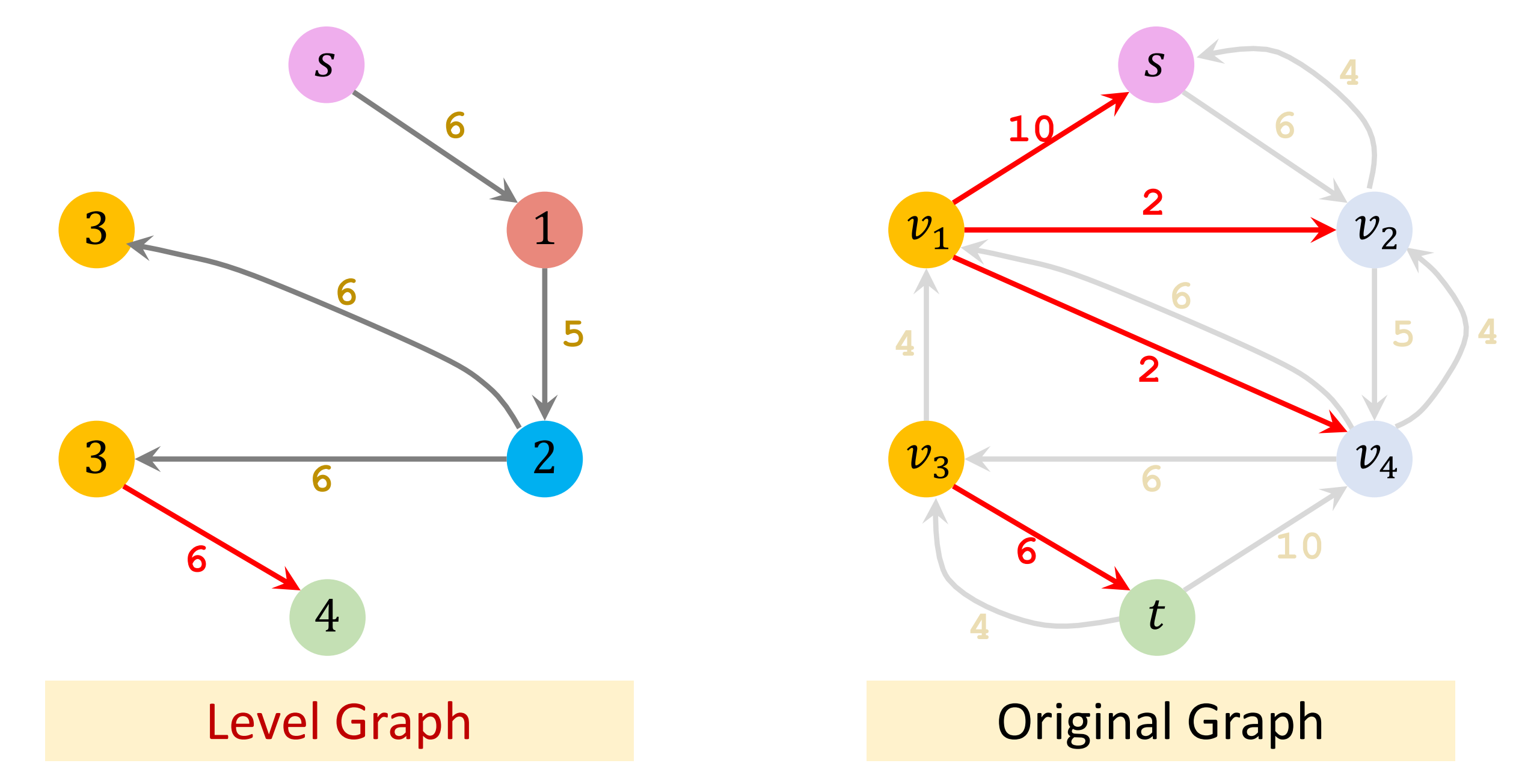
- Procedure
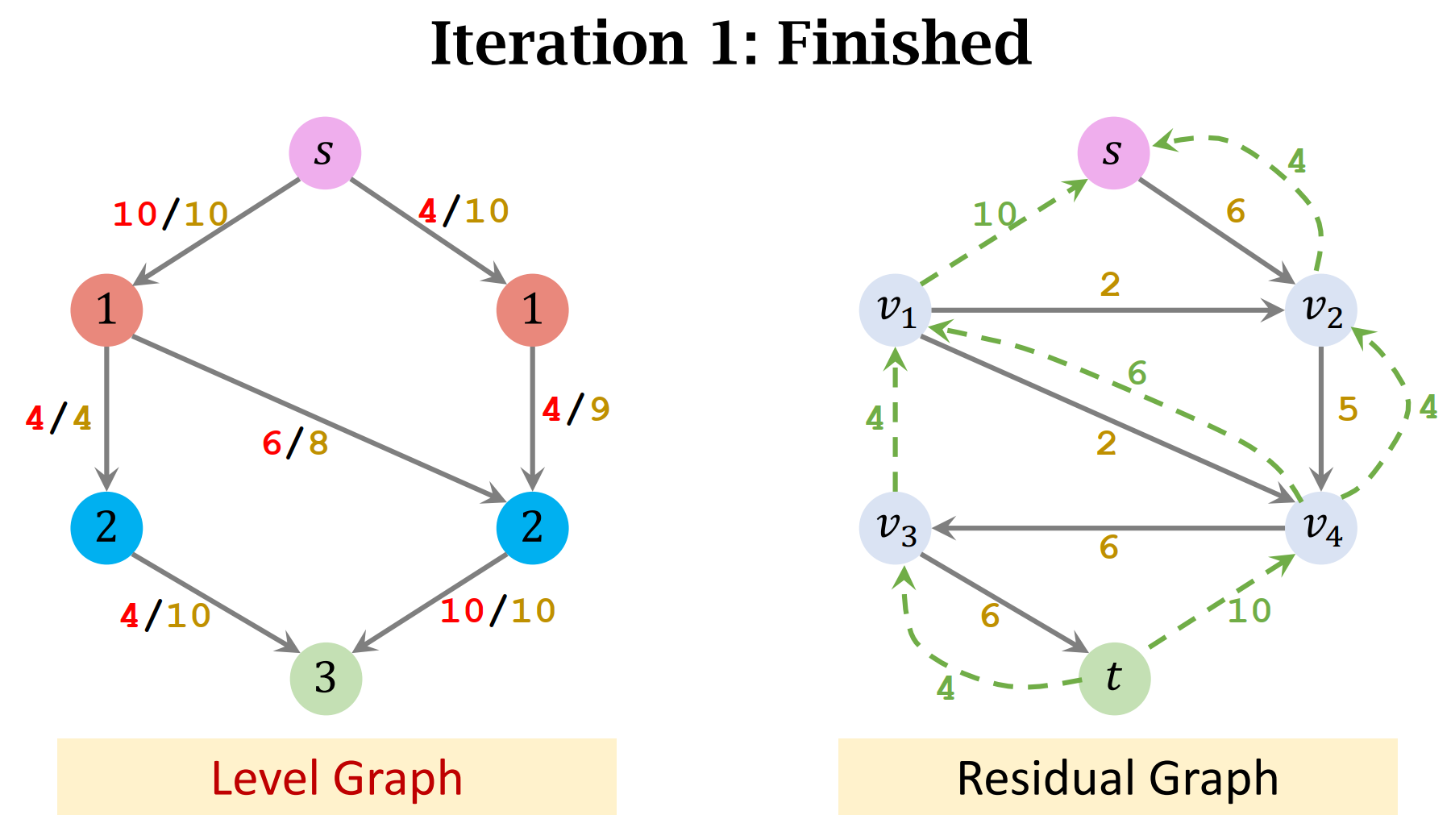
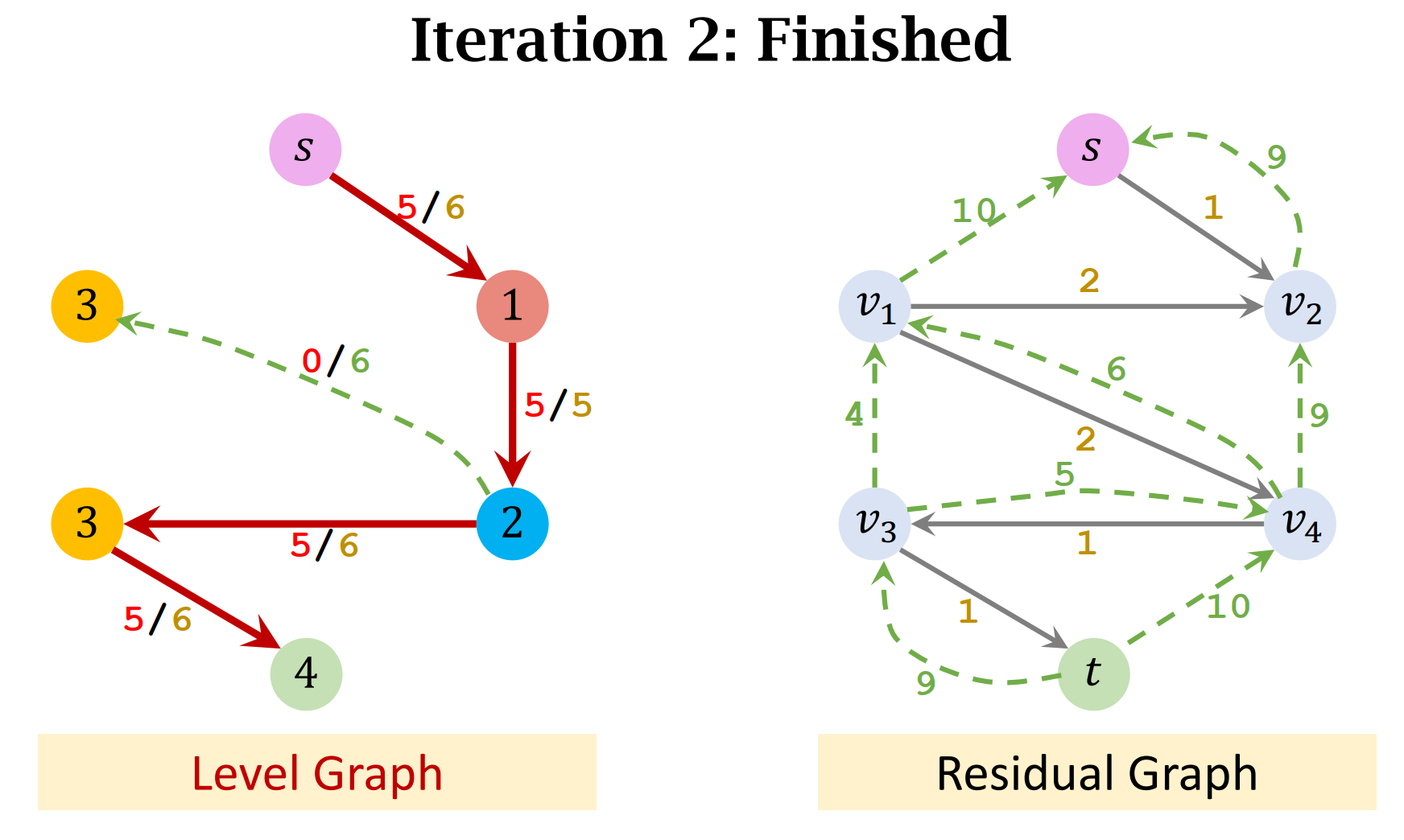
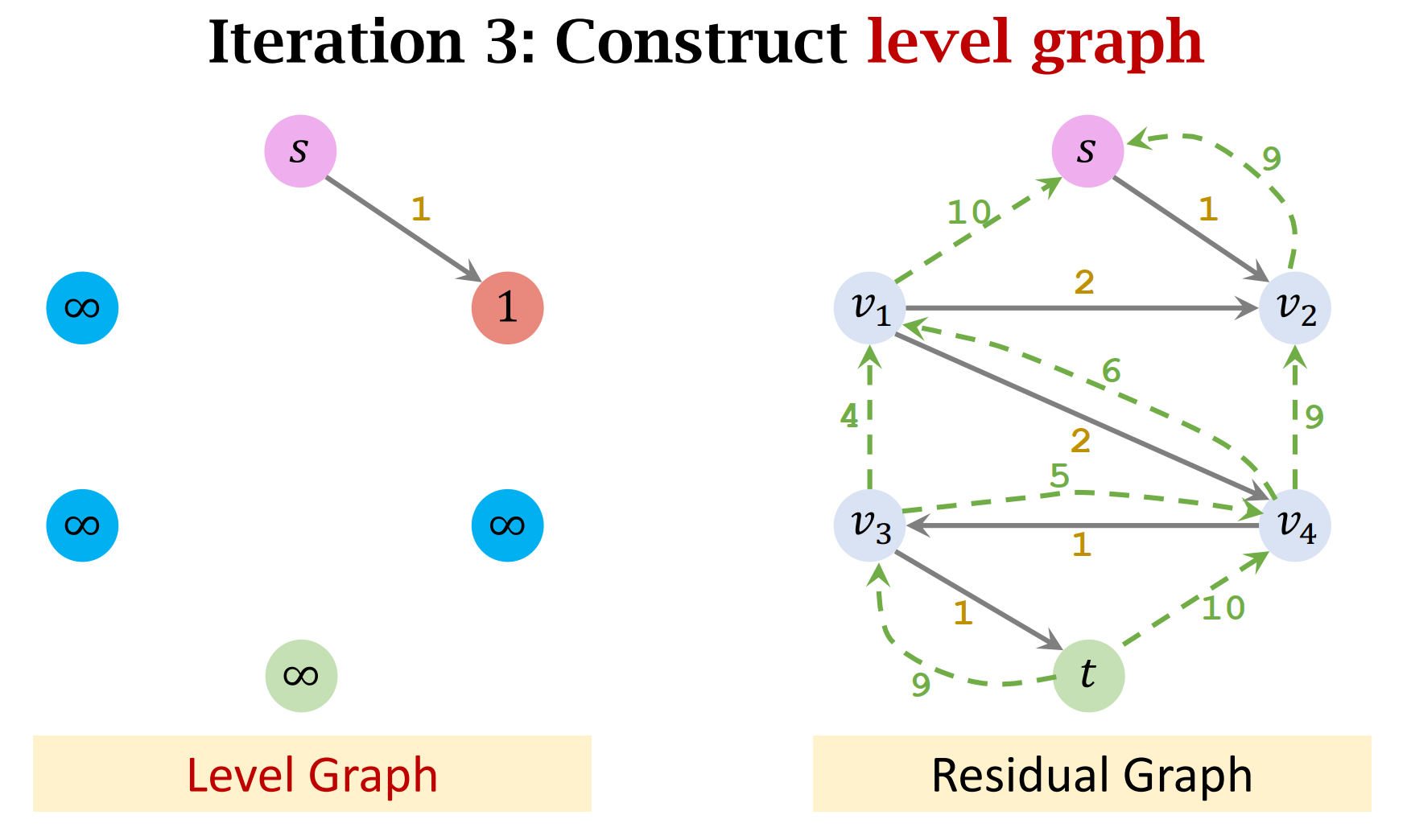
  - On the level graph, no flow can be found!
  - End of Procedure
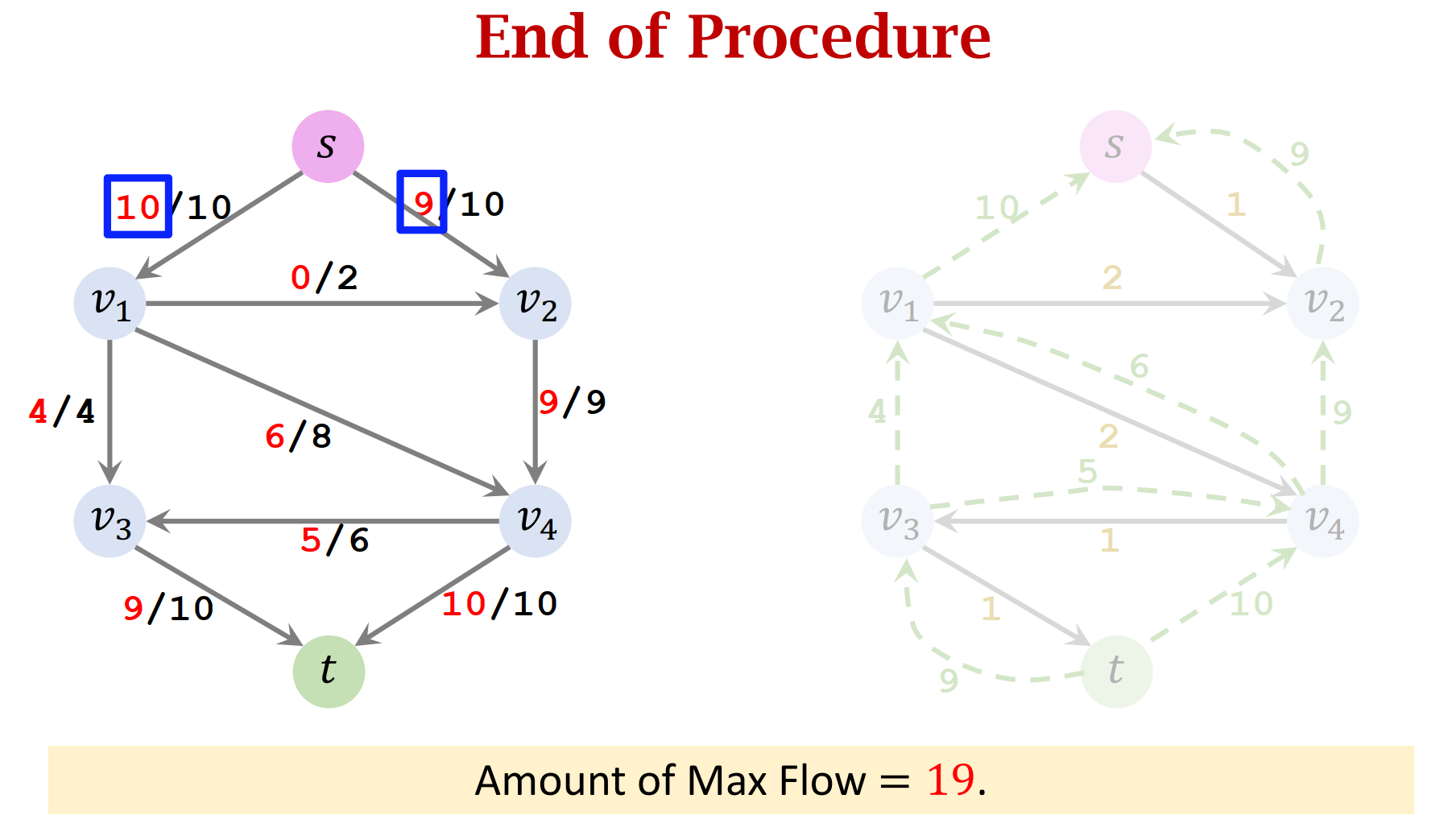
- Summary
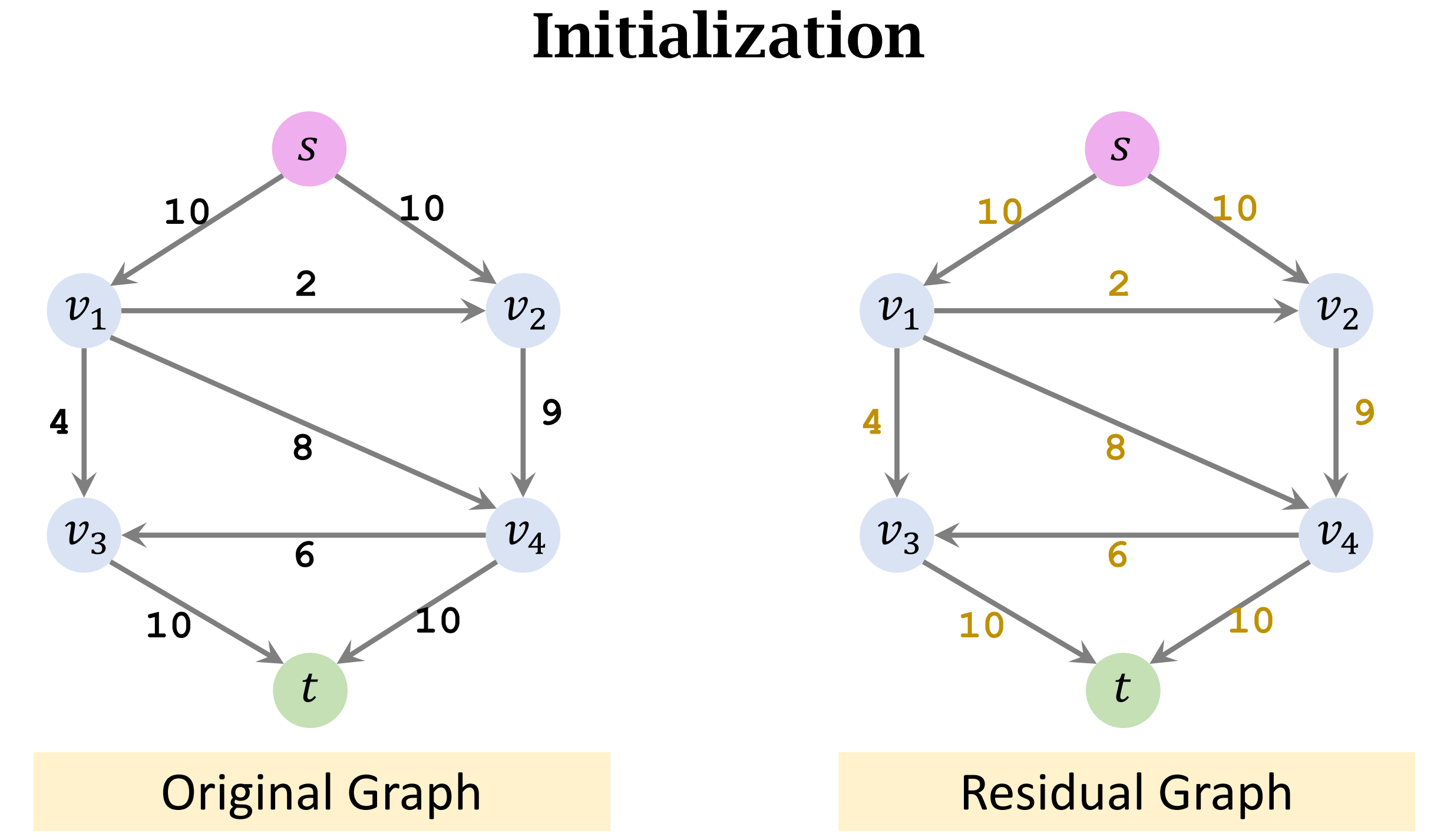
  1. Initially, the residual graph is a copy of the original graph.
  2. Repeat:
  3. Construct the level graph of the residual graph.
  4. Find a blocking flow on the level graph.
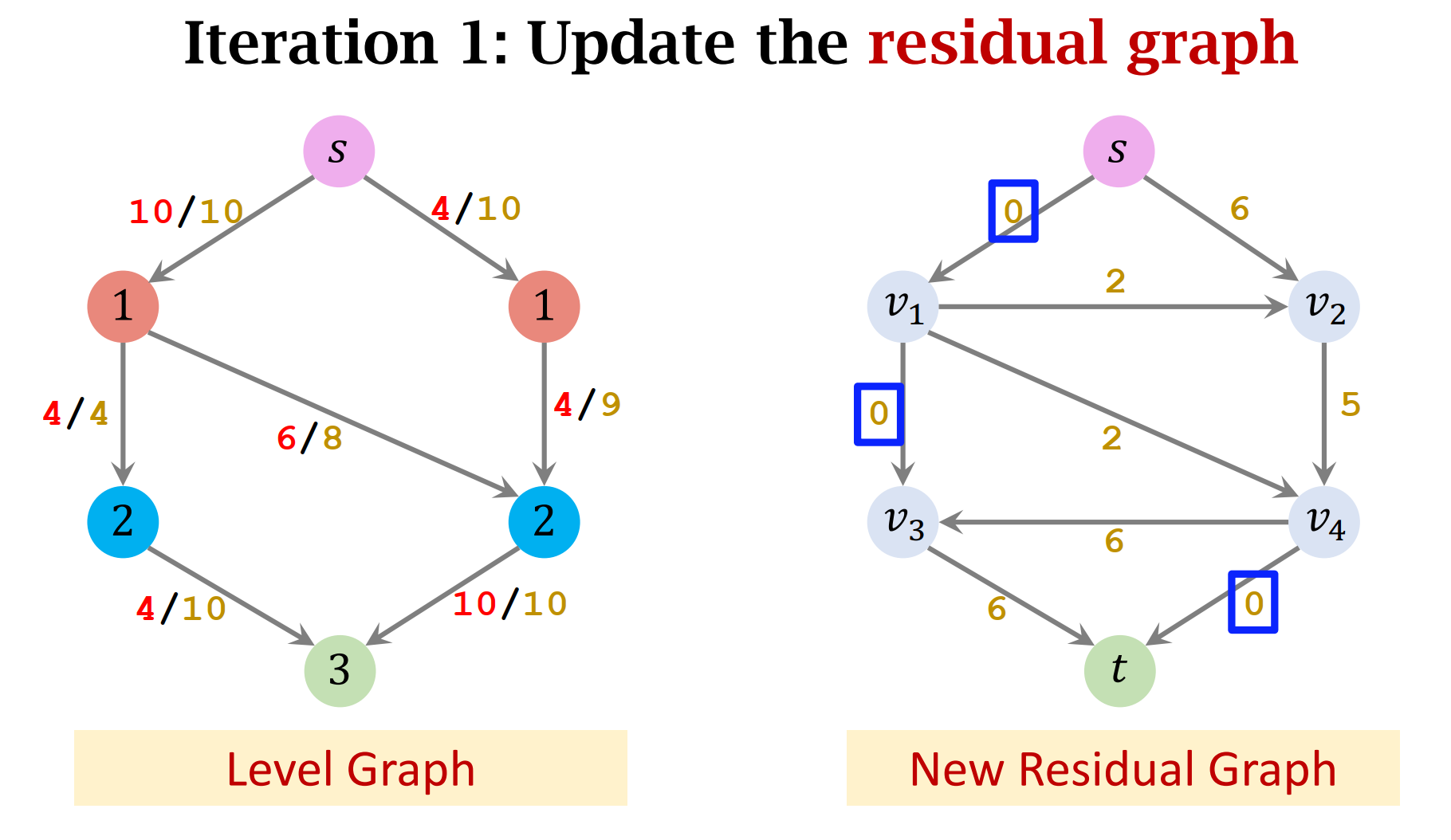
  5. Update the residual graph (update the weights, remove saturated edges, and add backward edges.)
- Time complexity: $O(m \cdot n^2)$ . (m is #edges; n is #vertices.)
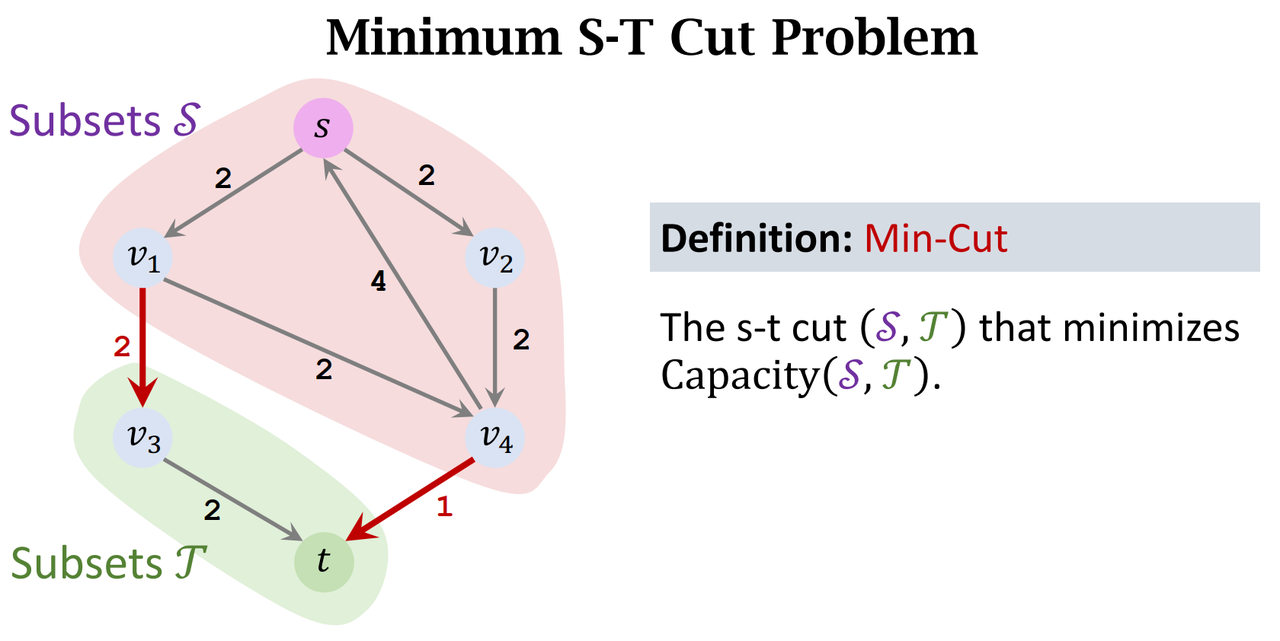
Minimum Cut Problem
- statement
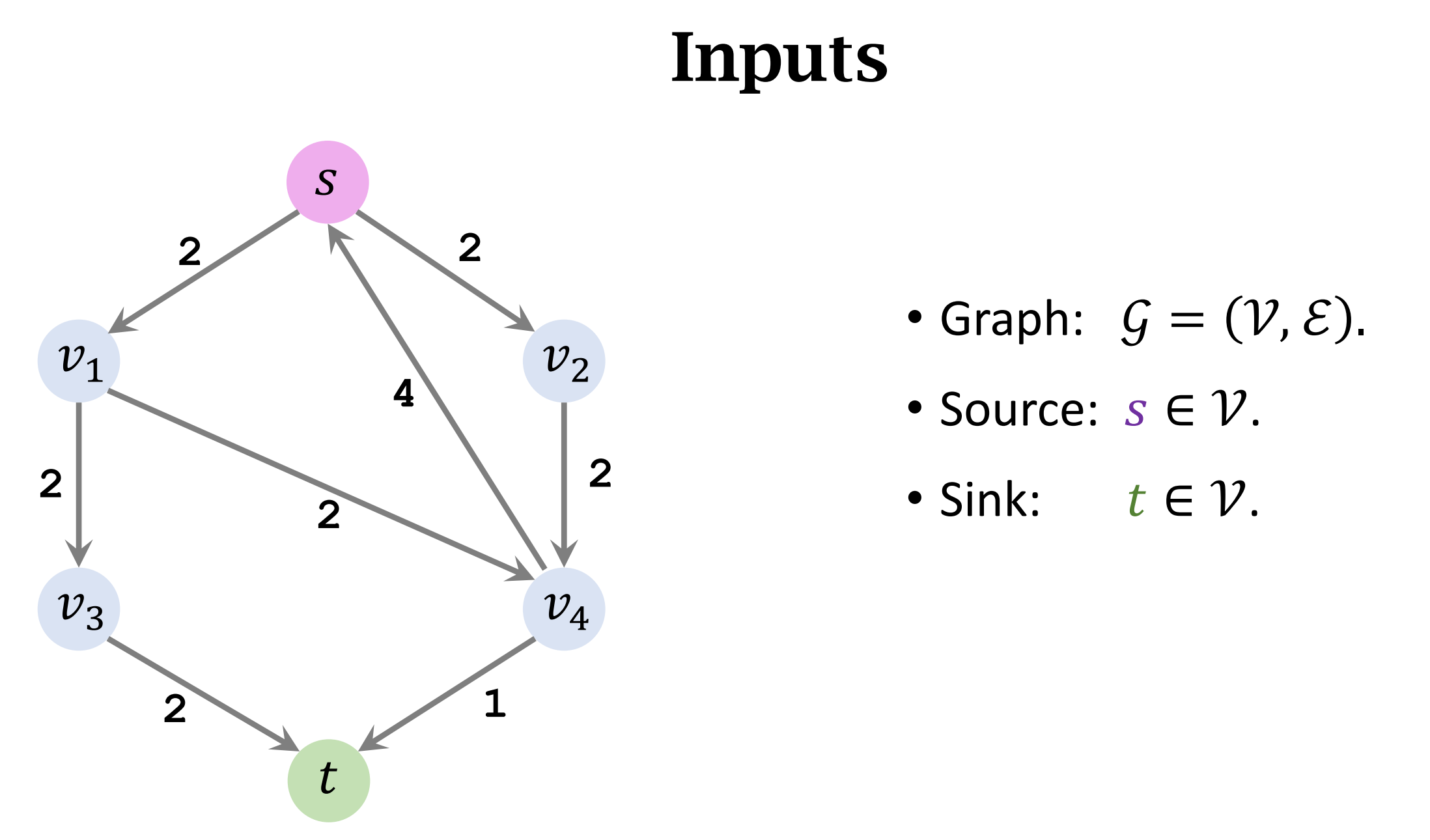
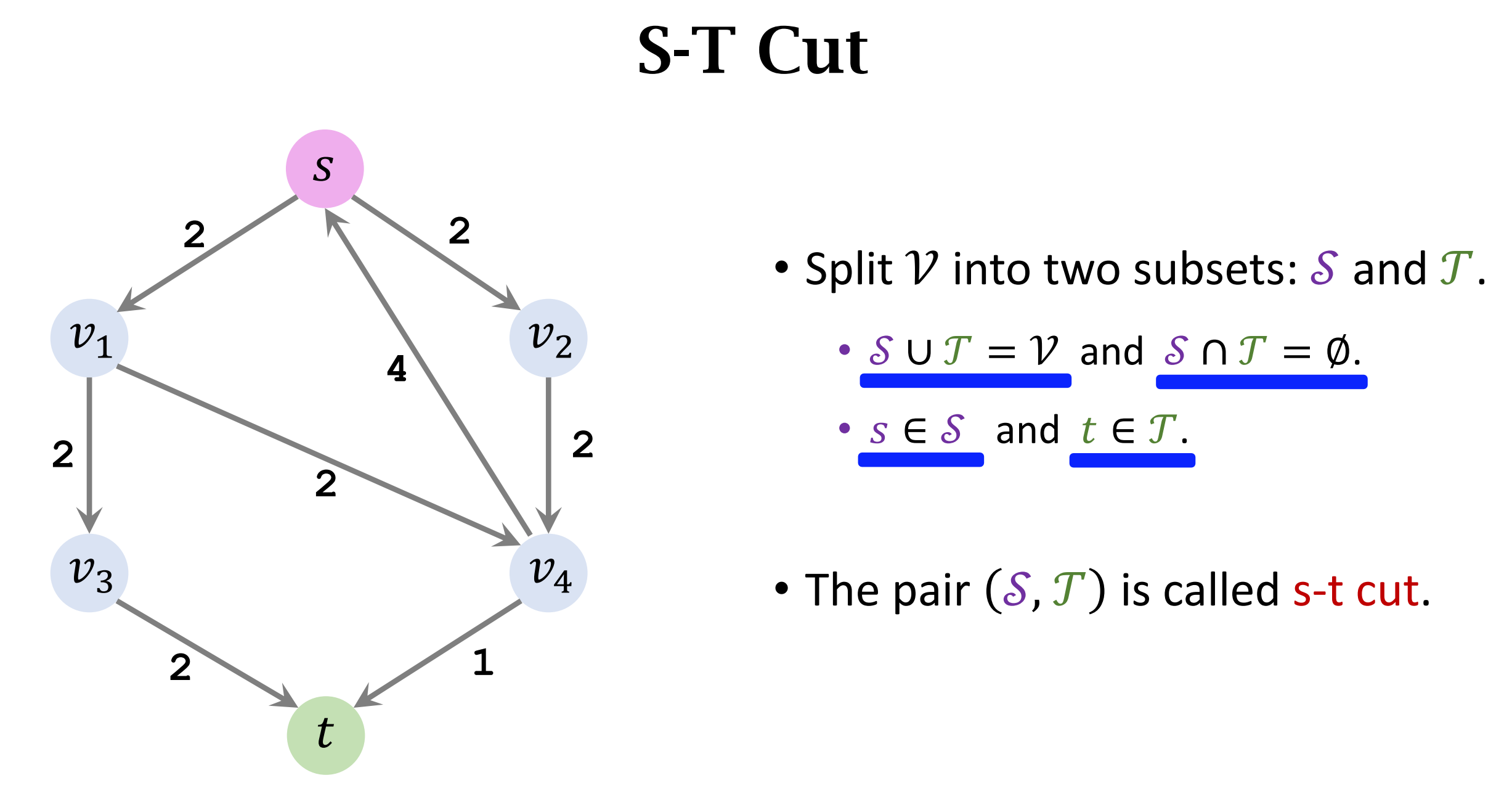
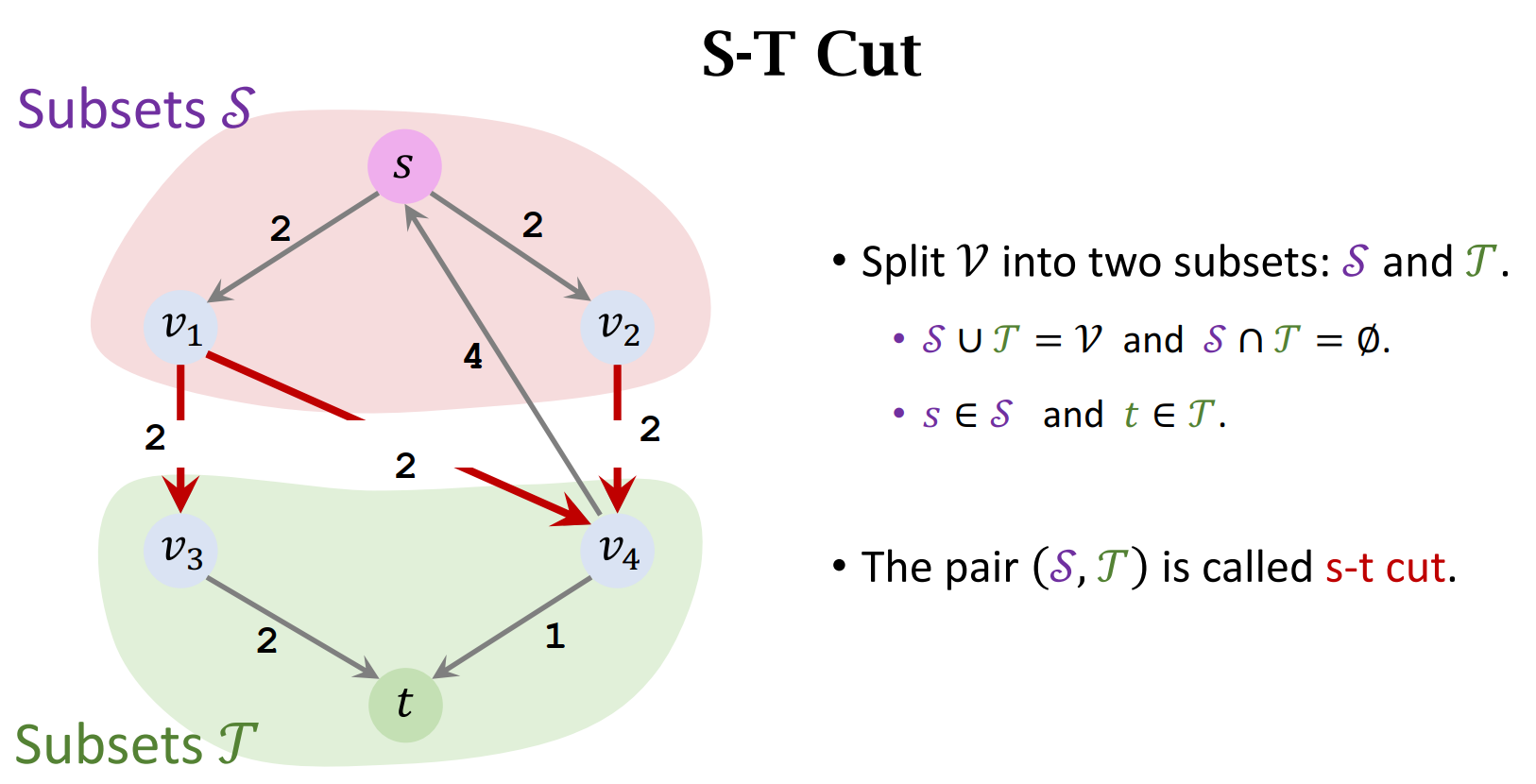
  - Capacity (S, T) = sum of weights of the edges leaving S.
  - In the figure, three edges leave S.
    - Capacity (S,T) = 2 + 2 + 2 = 6

- Max-Flow Min-Cut Theorem
- In a flow network, the maximum amount of flow from s to t is equal to the capacity of the minimum s-t cut.
- In short, amount of max-flow = capacity of min-cut.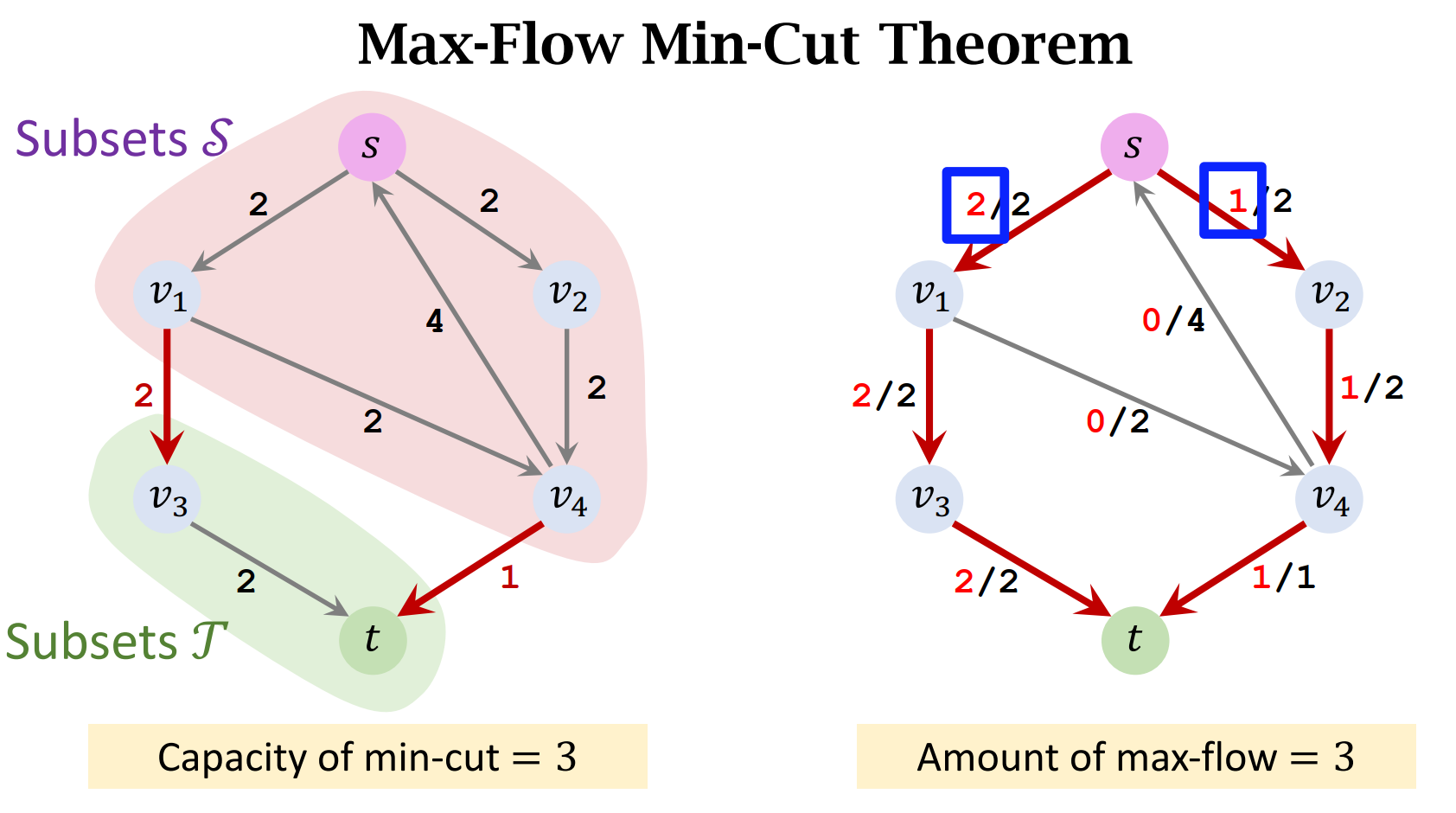

- Algorithm
- Run any max-flow algorithm to obtain the final residual graph.
- E.g., Edmonds–Karp algorithm or Dinic’s algorithm.
- Ignore the backward edges on the final residual graph
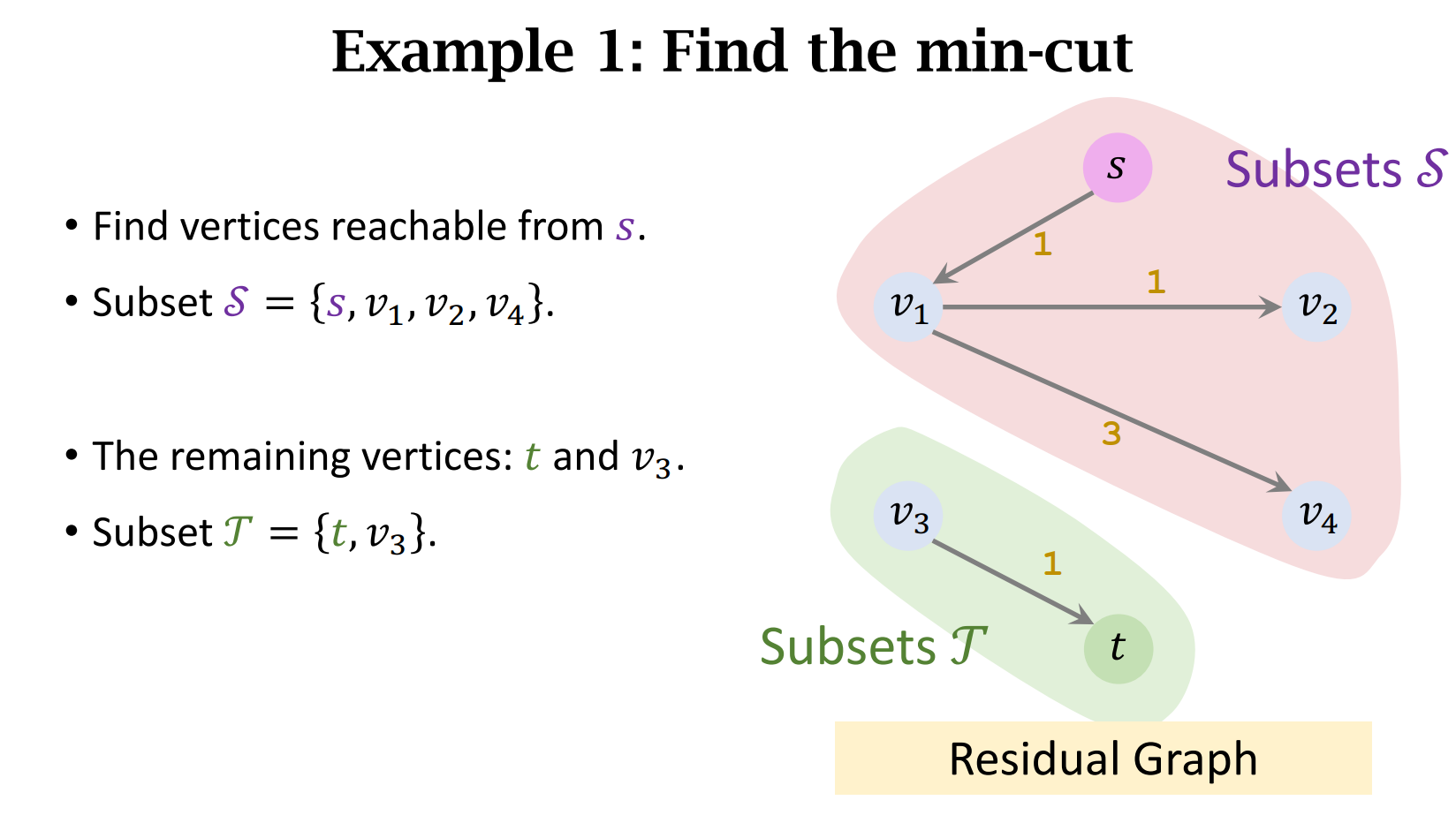
- Find the minimum s-t cut (S,T) :
- On the residual graph, find paths from source 𝑠 to all the other vertices.
- S ← all the vertices that have finite distance. (Reachable from s.)
- T ← all the remaining vertices. (Not reachable from s.)
- Example