MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记
Lecture 5: Commitment 1 (Ying Tong Lai)
- Overview: Modern SNARK
- IOP: Interactive Oracle Proof
- Commitment Scheme
- IOP “compiled by” the commitment scheme to get a non-interactive proof
- An IOP is “information-theoretic” in that it provides soundness and zero-knowledge guarantees even when the prover and verifier are computationally unbounded. To make this possible, the proof system makes the idealised assumption of “oracle access”: in other words, the verifier can only access the prover’s messages through random queries.
- The commitment scheme instantiates this oracle access using cryptographic primitives (e.g. a one-way function): as a consequence, the resulting argument system is only secure with respect to a computationally bounded prover and/or verifier. To realise a succinct argument system, the chosen commitment scheme must provide low communication complexity relative to the computation being proven.
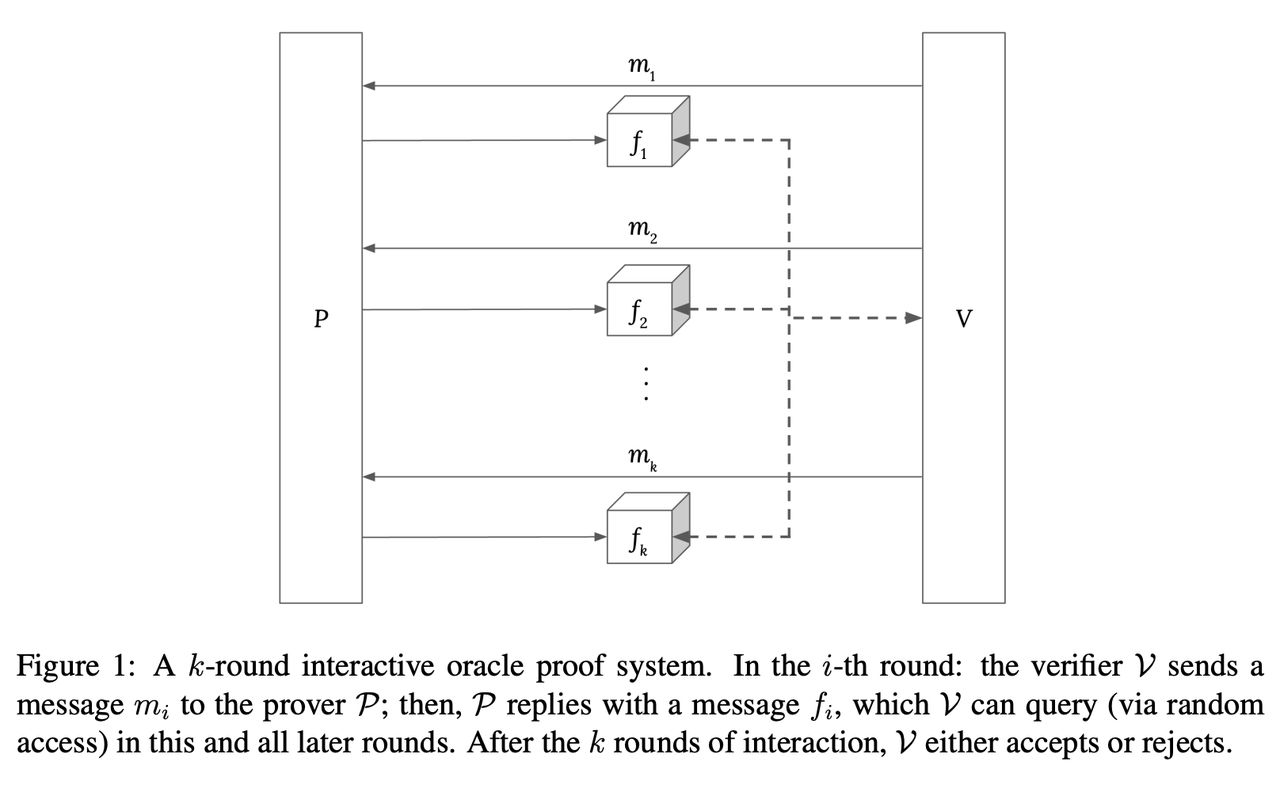
- Commitment Schemes
- Formal definition:

- The Open Algorithm can be divided into two part
- Prove(pp, C, m, r) -> $\pi$
- Verify(pp, C, $\pi$) -> {0,1}
- The Open Algorithm can be divided into two part
- Pederson Commitment

- Formal definition:
- Vector Commitment
- Vector Pedersen commitment.

- Merkle tree: A well-known solution for building vector commitments is a Merkle tree. It is used in distributed systems like Git, Cassandra, and Bitcoin for summarizing sets of data. Merkle trees also have hiding and extractability properties, which make them an ideal candidate for compiling an IOP into a non-interactive proof secure in the random oracle model.
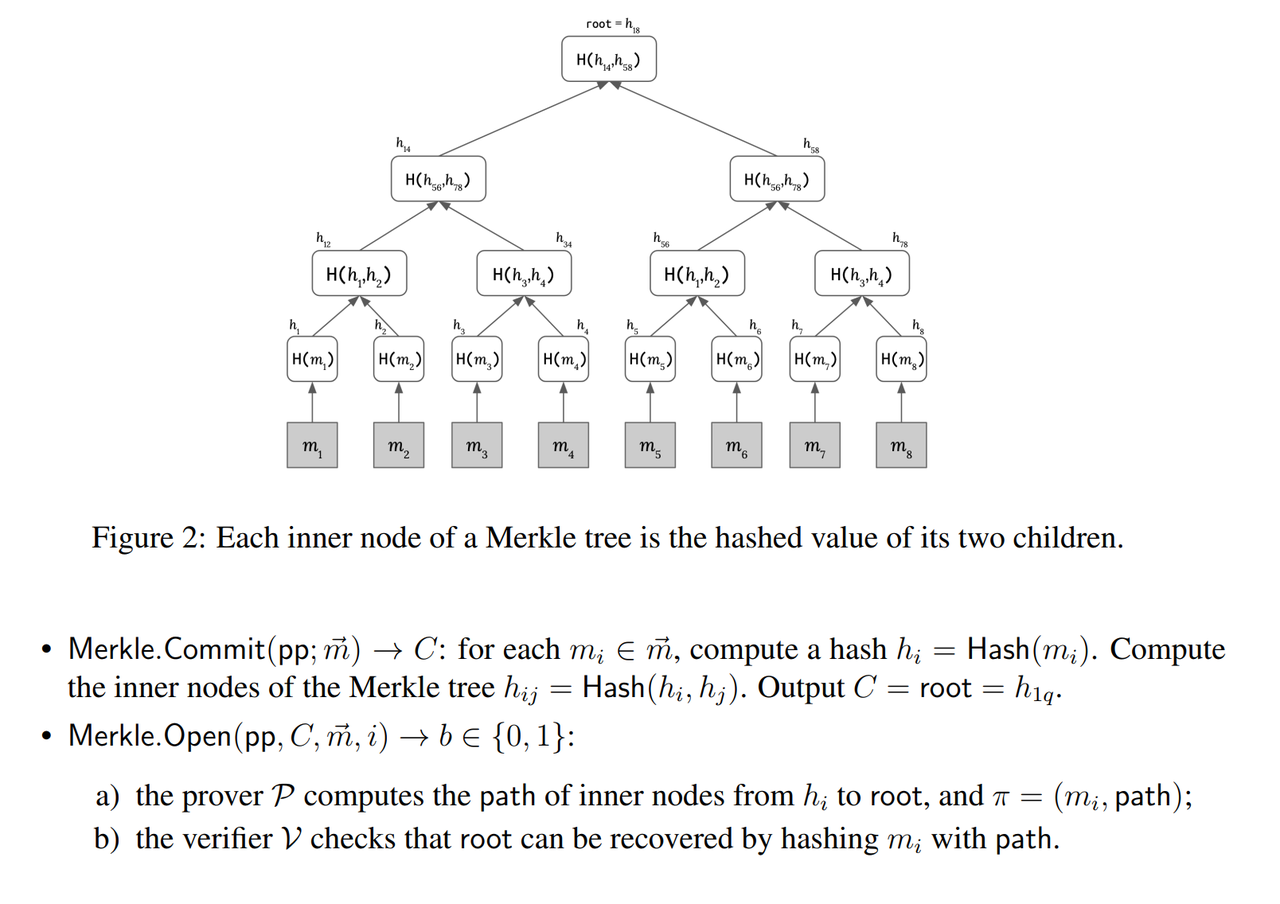
- The Merkle Tree Commitment proved that
- $m_i$ is an element in the vector $m$
- The root $h$ is the commitment of the vector $m$
- The Merkle Tree Commitment proved that
- Vector Pedersen commitment.