Lecture 3: Mathematical Building Blocks (Yufei Zhao)

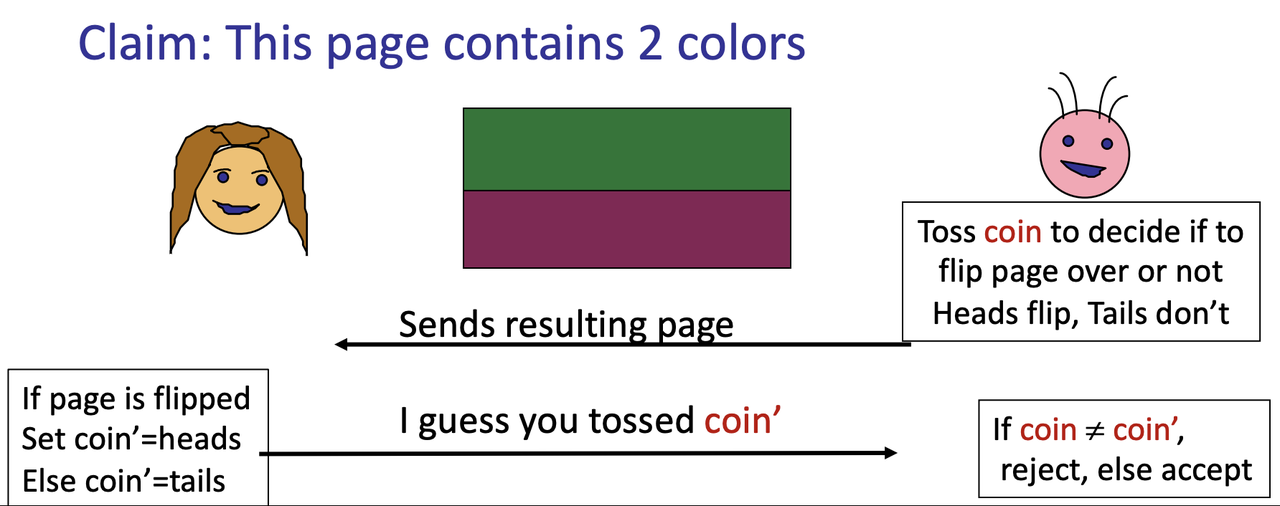
Example: I (Prover) want to convince you (Verifier) that I can distinguish two colors that you see as identical
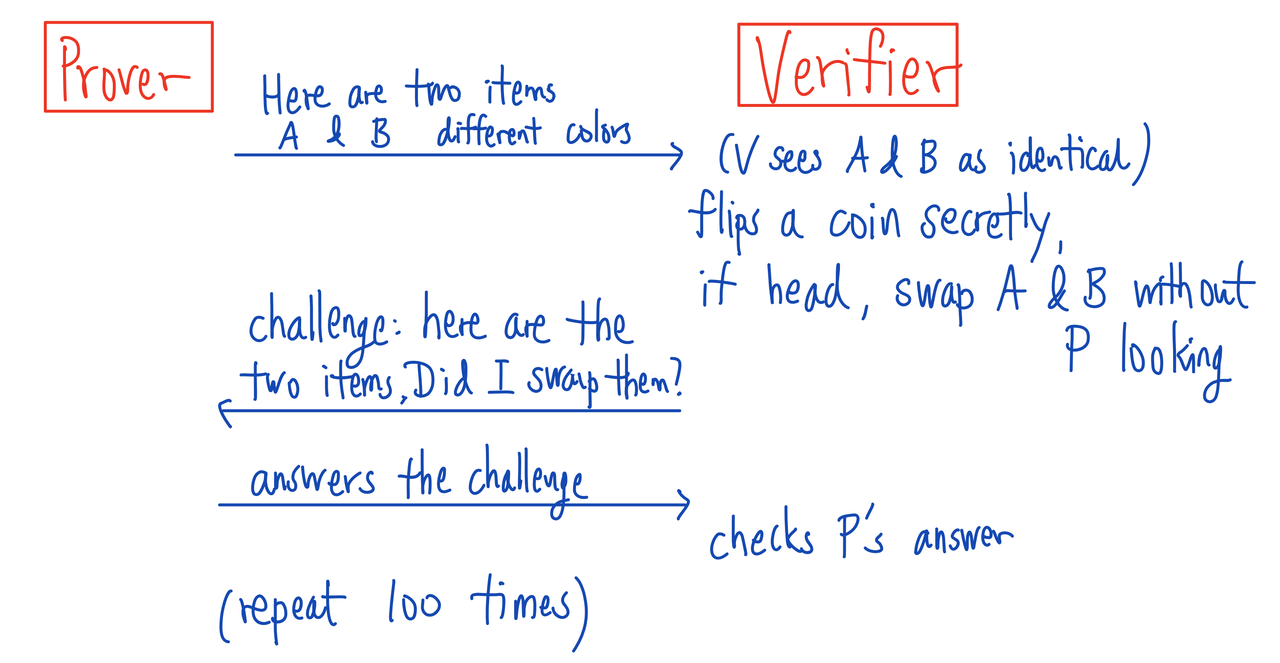
- A Similar Example: How to prove two colors are different to a blind verifier
- What is a proof?
  - A proof is something that could convince someone else
  - Properties: completeness, soundness, zero-knowledge
- What is the prover and the verifier (based on blockchain)
  - Prover: run on the regular computer (much more powerful than the verifier)
  - Verifier: run on the smart contract
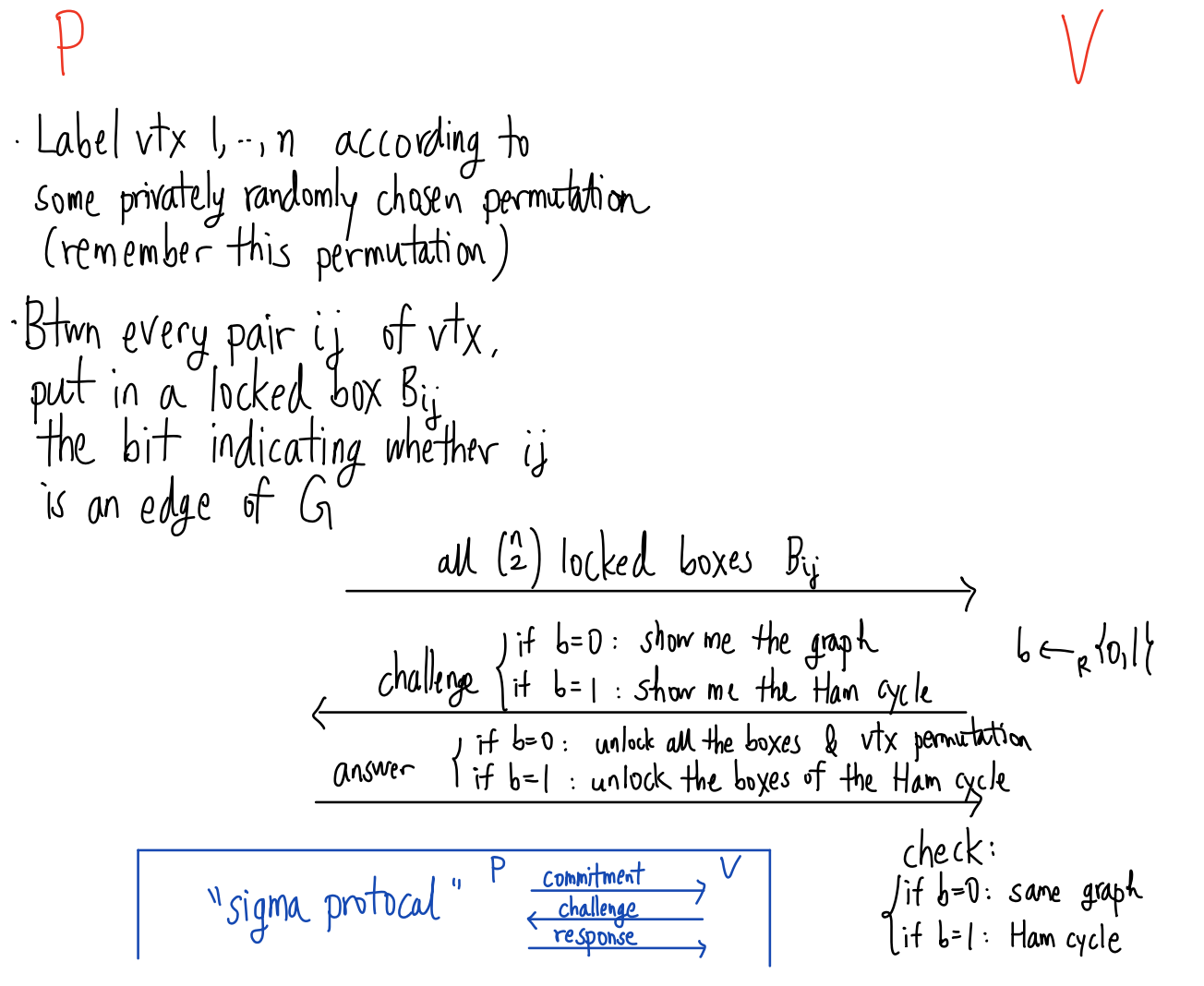
Example: Hamilton cycle [Blum ‘87]
- Hamilton cycle: a cycle can go through every vertex of the graph exactly once and return to the start
- Everybody knows a graph
- P knows a Hamilton cycle in the graph without revealing any additional information
- Protocol
ZKP Properties
- Completeness: If everyone behaves then protocol accepts
- Soundness: If there is no Ham cycle, then no matter what P does, V rejects with the probability of $\geq \frac{1}{2}$
  - There is a stronger requirement called knowledge soundness which says that even if the graph has a Ham Cycle , the prover doesn’t know it, the protocol will still fail. The precise definition involves an extractor with rewinding abilities.
- Zero-knowledge: If V accepts then it learns no addl into from the interaction because V could have simulated the entire dialog by itself.