MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记
Lecture 6: Algorithms for Efficient Cryptographic Operations (Jason Morton)
- Multi-scalar Multiplication(MSM)
- Naive: nP = (((P + P) + P) + P)… = (2(2P))…
- Binary expand
- $n = e_0+e_1\alpha+e_2\alpha^2+\dots+\e_{\lambda-1}^{\lambda-1}
- Accumulator
- Q = P;
- R = 0 if e_0 = 0
- R = P if e_0 = 1
- For i = 1 to t
- Q = 2Q
- If e_i = 1
- R = R+Q
- Return R
- Overhead: \log_2 n doubling + \log_2 n add
- Pippenger [Reference:drouyang.eth, https://hackmd.io/@drouyang/SyYwhWIso]
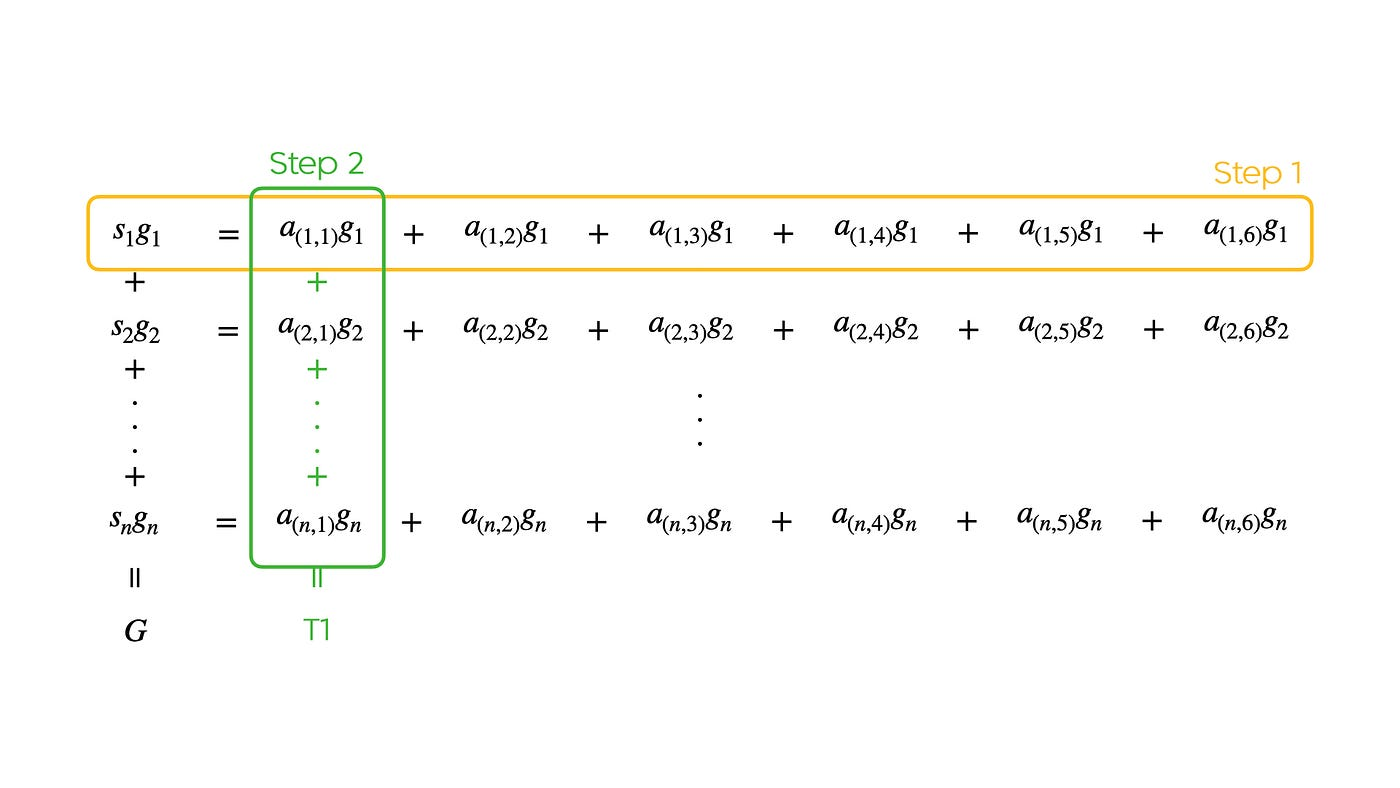
- $P=\sum_{i=0}^n k_i P_i$
- Step 1: partition scalars into windows
- Let’s first partition each scalar into $m$ windows each has $w$ bits, then
- $k_i = k_{i,0} + k_{i,1} 2^{w} + … + k_{i,(m-1)} 2^{(m-1)w}$
- You can think of each scalar $k_i$ as a bignum and representing it as a multi-precision integer with limb size $w$. Then we have,
- $\sum_i k_i P_i = \sum_i \sum_{j=0}^{m-1} k_{i,j} 2^{jw} P_i$
- By reordering the sums, we get
- $\sum_i k_i P_i= \sum_j 2^{jw} \left( \sum_i k_{i,j} P_i \right) = \sum_j 2^{jw} W_j$
- It means we can calculte the MSM for each window $W_j$ first, then aggregate the results
- Then, let’s examine $W_j = \sum_{i=0}^n k_{i,j} P_i$
- Let’s first partition each scalar into $m$ windows each has $w$ bits, then
- Step 2: for each window, add points by bucket
- Because each window has $w$ bits, $k_{i,j}$ has a value range of $[0, 2^w-1]$.Therefore, we can put $n$ points into $2^w$ buckets according to the value of $k_{i,j}$. We can first calculate $W_j$ by,
- for bucket $t$, $t \in {0, 2^w-1}$, calculate the sum of points in this bucket and get $B_t$.
- $W_j = \sum_{t=0}^{2^w-1} t B_t$
- Because each window has $w$ bits, $k_{i,j}$ has a value range of $[0, 2^w-1]$.Therefore, we can put $n$ points into $2^w$ buckets according to the value of $k_{i,j}$. We can first calculate $W_j$ by,
- Step 3: reduce window results
- $P=\sum_{i=0}^n k_i P_i = \sum_j 2^{jw} W_j$