MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记
Lecture 3: Mathematical Building Blocks (Yufei Zhao)
- Fiat Shamir heuristic
- Turn an interactive proof to a non-interactive proof
- P can simulate V
- whenever V picks a random value
- P can simulate V’s randomness by running a cryptographic hash function on the transcript so that P can’t cheat by choosing “favorable random challenges”
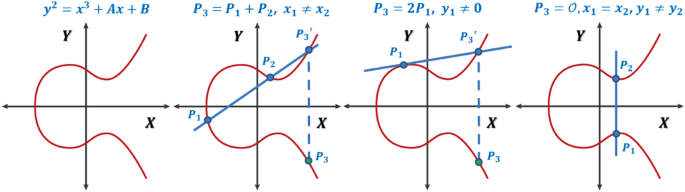
- Elliptic Curve
- $y^2 = x^3 + Ax + B$
- All points in a elliptic curve make a group
- g in the generator of the group G

- Difficult problem:
- Discrete Log Problem on Elliptic Curve
- Secret random x generated form Zq
- Share with the public xG
- It is hard to recover x from xG
- Diffie-Hellman Key Exchange (Public key cryptography)
- Alice takes a random a mod q
- Bob takes a random b mod q
- Alice says to the public: aG
- Bob says to the public: bG
- So, Alice and Bob share a secret: abG
- Discrete Log Problem on Elliptic Curve
- Pairing based cryptography
- Given cyclic groups $G_0, G_1, G_T$ all same prime order q
- a pairing is a nondegenerate bilinear map
- $e: G_0 \times G_1 \rightarrow G_T$
- Properties
- Bilinear
- e(x+x’, y) = e(x,y) + e(x’,y)
- e(x,y+y’) = e(x,y) + e(x,y’)
- e(ax,y) = ae(x,y) + e(x,ay)
- Nondegenerated
- With generator $g_0 \in G_0$ and $g_1 \in G_1$
- $g_T = e(g_0, g_1) \in G_T$
- Bilinear
- An application BLS signature scheme (Boneh-Lynn-Shacham)
- Protocol
- Keygen: $sk = s$, $pk = sg$
- Sign(sk,m): $\sigma = sH(m)$
- Verify(pk,m): check $e(pk, H(m)) = e(g,\sigma)$
- It can be extended to allow signature aggregation
- The verifier can collect all the signatures and aggregate them into a single short signature.
- The verifier can just verify the short signature then he knows that everyone signed their messages correctly.
- Protocol