Sigma Protocol
Introduction
Sigma protocols are a specific type of interactive zero-knowledge proof (ZKP) that are known for their efficiency and simplicity.
They involve three distinct phases between a prover and a verifier:
- Prover: $P(x,y)$
- Verifier: $V(y)$
- Commitment: The prover sends an initial commitment $t$ to the verifier, often involving a secret value.
- Challenge: The verifier responds with a random challenge $c$.
- Response: The prover calculates a response $z$ based on the challenge and their secret knowledge and sends it to the verifier.
- Evaluation: Upon receiving prover’s response $z$, the verifier outputs either accept or reject, which must be computed strictly as a function of the statement $y$ and the conversation $(t,c,z)$. In particular, the verifier does not make any random choices other than the selection of the challenge: all other computations are completely deterministic.
Example: Okamoto’s protocol
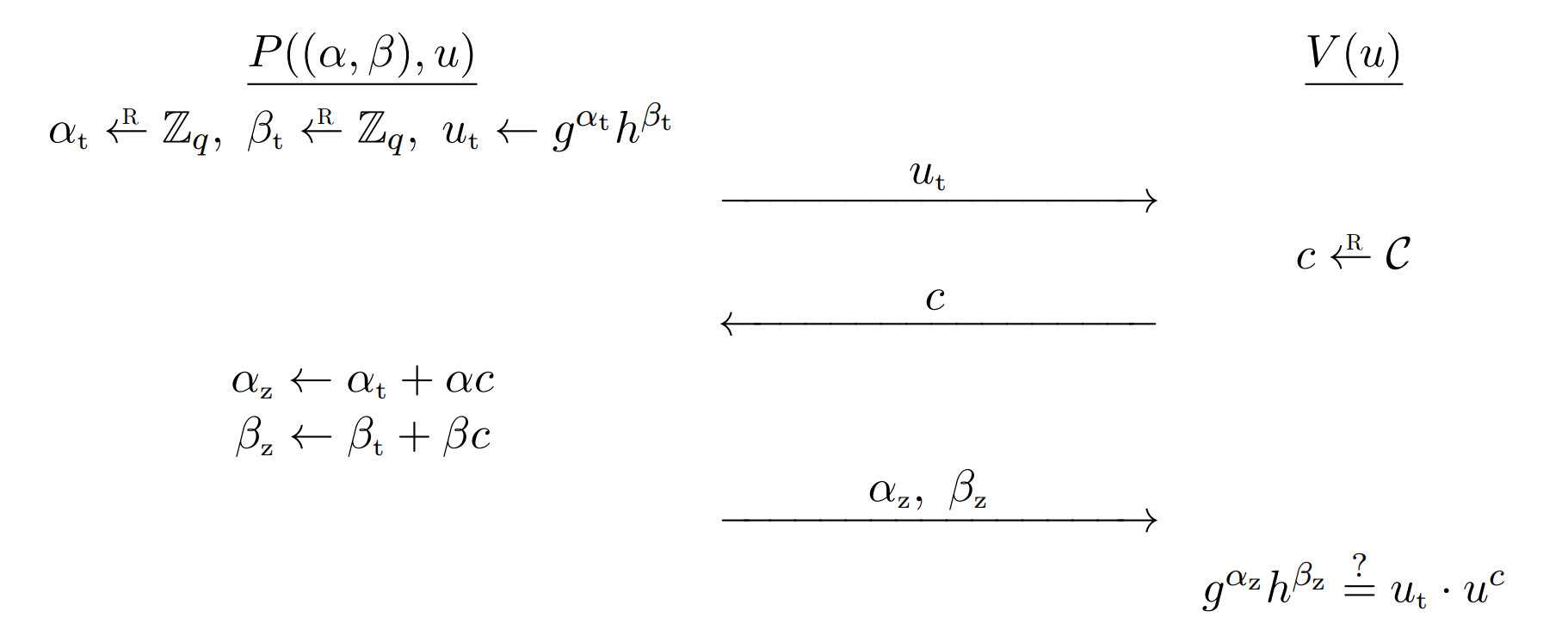
Okamoto’s protocol allows a prover to convince a skeptical verifier that he “knows” a representation of a given $u \in \mathbb{G}$, without revealing anything about that representation to the verifier.
A witness for the statement $u \in \mathbb{G}$ is $(\alpha; \beta) \in \mathbb{Z}_q^2$such that $g^{\alpha}h^{\beta} = u$, i.e., a representation of $u$. Thus, in this example, every statement has many witnesses.
- Prover: $P((\alpha, \beta), u)$
- Verifier: $V(u)$
- The prover computes $\alpha_t \leftarrow \mathbb{G}$, $\beta_t \leftarrow \mathbb{G}$, $u_t \leftarrow g^{\alpha_t}h^{\beta_t}$ and sends the commitment $u_t$ to the verifier.
- The verifier computes a random $c$ and sends the challenge $c$ to the prover.
- The prover computes $\alpha_z \leftarrow \alpha_t + \alpha c \in \mathbb{Z}_q$, $\beta_z \leftarrow \beta_t + \beta c \in \mathbb{Z}_q$ and sends the response $(\alpha_z, \beta_z)$ to the verifier.
- The verifier checks if $g^{\alpha_z}h^{\beta_z} = u_t \cdot u^c$. if so, the verifier outputs “accept”; otherwise, the verifier outputs “reject”.