The Chaum-Pedersen Protocol
Introduction
The Chaum-Pedersen protocol allows a prover to convince a skeptical verifier that a given triple is
a DH-triple, without revealing anything else to the verifier.
Let $\mathbb{G}$ be a cyclic group of prime order $q$ generated by $g \in \mathbb{G}$. For $\alpha, \beta, \gamma \in \mathbb{Z}_q$, we say that $(g^{\alpha}, g^{\beta}, g^{\gamma})$ is a DH-triple if $\alpha\beta = \gamma$. Equivalently,$(u, v, w)$ is a DH-triple if and only if there exists $\beta \in \mathbb{Z}_q$ such that $v = g^{\beta}$ and $w = u^{\beta}$
Explain: Why the two definitions are equivalent?
- For the first definition, $e(g^{\alpha}, g^{\beta}) = e(g^{\gamma}, g)$.
- For the second definition, we set $u = g^{\alpha}$. Left side $= e(u, g^{\beta}) = e(g^{\alpha}, g^{\beta})$. Right side $= e(u^{\beta},g) = e(g^{\alpha \beta}, g) = e(g^{\gamma},g)$. Left side $=$ Right side.
Protocol Details
- Prover: $(\beta, (u, v, w))$
- Verifier: $(u, v, w)$
- The prover computes $\beta_t \leftarrow \mathbb{Z}_q$, $v_t \leftarrow g^{\beta_t}$, $w_t \leftarrow u^{\beta_t}$ and sends the commitment $v_t$ and $w_t$ to the verifier.
- The verifier computes a random $c$ and sends the challenge $c$ to the prover.
- The prover computes $\beta_z \leftarrow \beta_t + \beta c$ sends the response $\beta_z$ to the verifier.
- The verifier checks if $g^{\beta_z} = v_t \cdot v^c$ and $u^{\beta_z}= w_t \cdot w^c$. if so, the verifier outputs “accept”; otherwise, the verifier outputs “reject”.
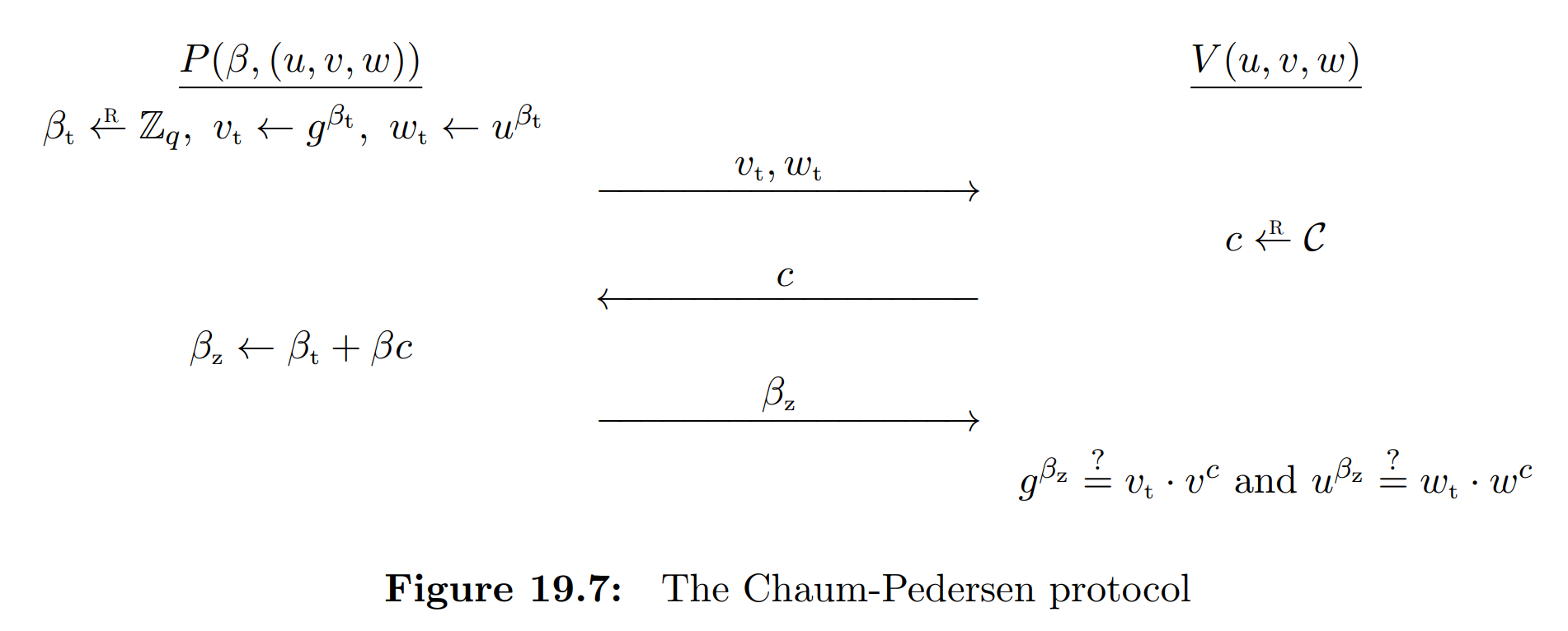
Why is it correct?
Explanation: The correctness of the Chaum-Pedersen Protocol is established through two key checks. Firstly, the verification “$g^{\beta_z} = v_t \cdot v^c$” ensures that the correlation between $v$ and $\beta$ mirrors that of $v^t$ and $\beta^t$. Similarly, the second verification “$u^{\beta_z} = w_t \cdot w^c$” confirms that the relationship between $w$ and $\beta$ aligns with that of $w^t$ and $\beta^t$. Since the prover is assumed to be honest, the veracity of $v_t \leftarrow g^{\beta_t}$ and $w_t \leftarrow u^{\beta_t}$ holds. Consequently, the relationships among $(u, v, w)$ are analogous, implying that $(u, v, w)$ forms a DH-triple.