A Sigma Protocol For Arbitrary Linear Relations
Definition
Observant readers may have discerned a notable resemblance among the Schnorr, Okamoto, and Chaum-Pedersen protocols. In truth, these protocols share a commonality—they all represent special cases of a generic Sigma protocol designed for proving linear relationships among group elements. This recognition underscores the conceptual unity underlying these cryptographic protocols, as they leverage a foundational structure to establish the validity of linear relations within the context of group-based cryptographic systems.
As usual, let $\mathbb{G}$ be a cyclic group of prime order $q$ generated by $g \in \mathbb{G}$. We shall consider boolean formulas $\phi$ of the following type:
$$
\phi(x_1, \dots, x_n) = \bigg{\Pi_{j=1}^n {g_1}{j}^{x_j} = $u_1$ \and \dots \and \Pi{j=1}^n {g_m}_{j}^{x_j} = $u_m$ \bigg}
$$
In such a formula $\phi$, the $g_{ij}$’s and $u_i$’s are elements of the group $\mathbb{G}$. Some of these group elements could be system parameters or even constants, while others are specific to the formula. The $x_i$’s are the formal variables of the formula. When we assign values in $\mathbb{Z}_q$ to the variables $x_1, \dots, x_n$, the formula evaluates to true if all the equalities above holds.
The Detailed Protocol
- Prover: $P()$
- Verifier: $V()$
- The prover computes $\alpha_t \leftarrow \mathbb{G}$, $\beta_t \leftarrow \mathbb{G}$, $u_t \leftarrow g^{\alpha_t}h^{\beta_t}$ and sends the commitment $u_t$ to the verifier.
- The verifier computes a random $c$ and sends the challenge $c$ to the prover.
- The prover computes $\alpha_z \leftarrow \alpha_t + \alpha c \in \mathbb{Z}_q$, $\beta_z \leftarrow \beta_t + \beta c \in \mathbb{Z}_q$ and sends the response $(\alpha_z, \beta_z)$ to the verifier.
- The verifier checks if $g^{\alpha_z}h^{\beta_z} = u_t \cdot u^c$. if so, the verifier outputs “accept”; otherwise, the verifier outputs “reject”.
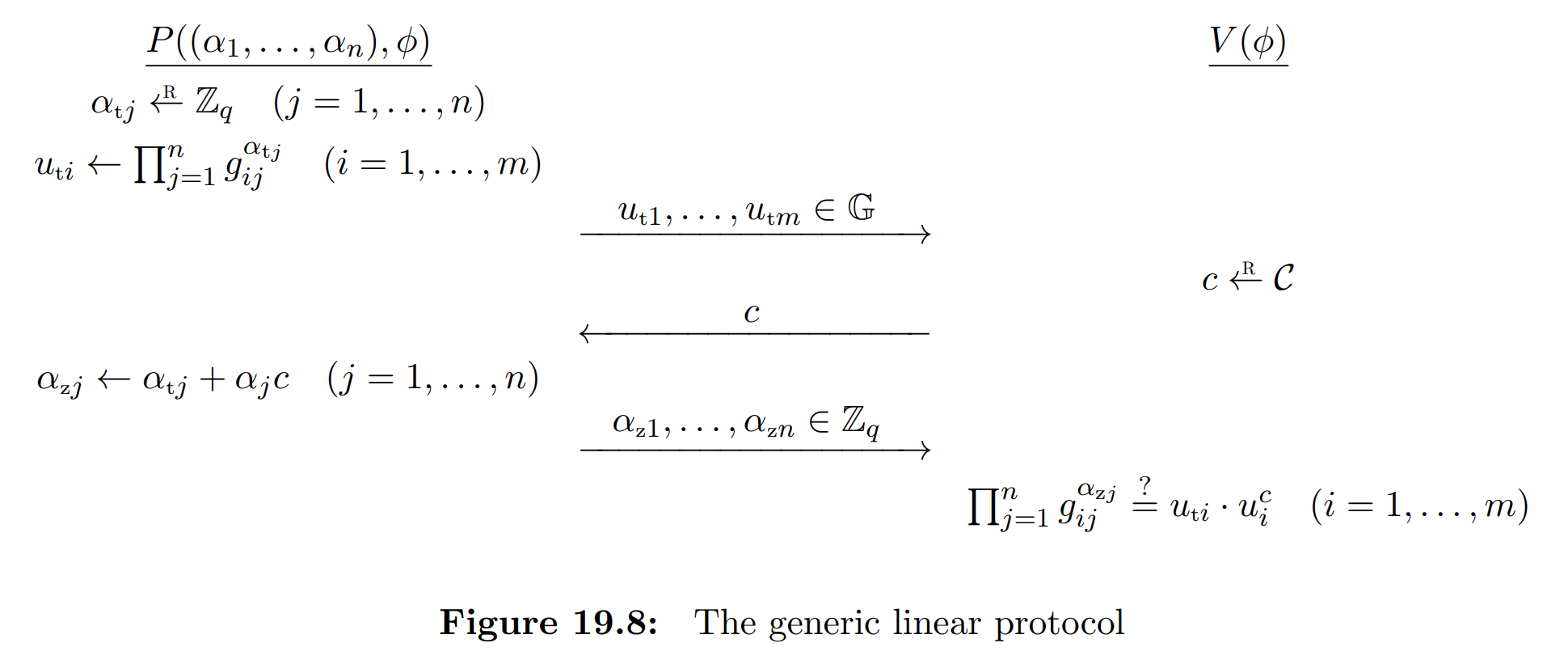
Special Cases
All the Sigma protocols presented so far are special cases of the generic linear protocol:
- Schnorr’s protocol is a special case with $\phi_1(x) = {u=g^x}$.
- Okamoto’s protocol is a special case with $\phi_2(x,y) = {u=g^xh^y}$.
- The Chaum-Pedersen protocol is a special case with $\phi_3(x) = {v=g^x \and w=u^x}$.