Freivalds’ Algorithm
Freivalds, Rusins. “Probabilistic Machines Can Use Less Running Time.” IFIP congress. Vol. 839. 1977.
Problem Statement
Suppose we are given as input two $n \times n$ matrices $A$ and $B$ over $\mathbb{F}_p$, where $p > n^2$ is a prime number. The fastest known algorithm for accomplishing this task in time roughly $\mathcal{O}(n^{2.37286})$.
Suppose someone hands us a matrix $C$. Our goal is to check whether or not the product matrix $A \cdot B = C$ in $\mathcal{O}(n^{2})$ time.
Algorithm
First, choose a random $r \in \mathbb{F}_p$, and let $x = (1,r,r^2,…,r^{n−1})$. Then compute $y =Cx$ and $z = A \cdot Bx$, outputting $1$ if $y = z$ and $0$ otherwise.
Time Cost
- vector $x = (1,r,r^2,…,r^{n−1})$ can be done with $\mathcal{O}(n)$ total multiplication operations.
- Multiply an $n \times n$ matrix by an n-dimensional vector can be done in $\mathcal{O}(n^{2})$ time.
2.1. $y = Cx$ : $\mathcal{O}(n^{2})$ time
2.2. $w = Bx$ : $\mathcal{O}(n^{2})$ time
2.3. $z = Aw$ : $\mathcal{O}(n^{2})$ time
Explaination
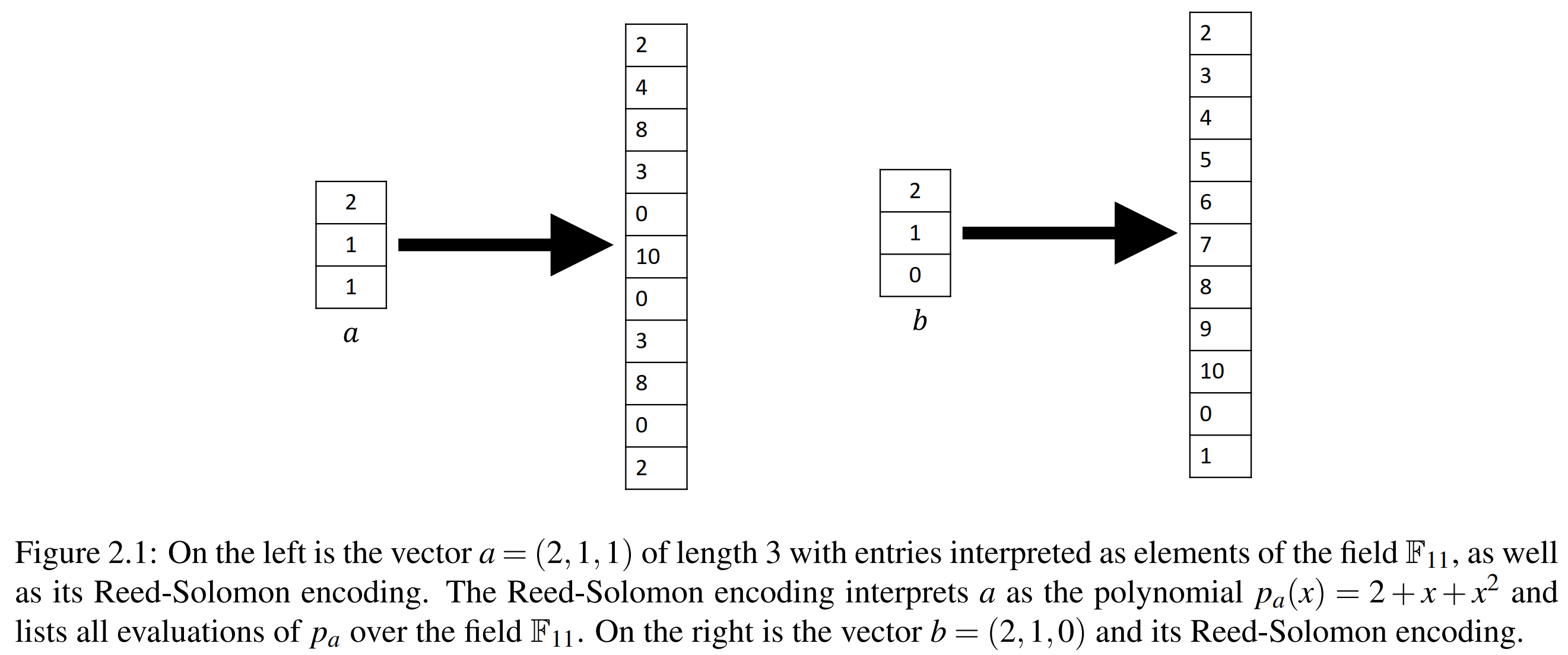
Recall the Reed-Solomon Fingerprinting: Encode vector $a$ and $b$ with Reed-Solomon Encoding: $p_a(x) = \sum_{i=1}^na_ir^{i-1}$,$p_b(x) = \sum_{i=1}^nb_ir^{i-1}$. If $a_i = b_i$ for all $i = 1,…,n$, then $p_a(r)=p_b(r)$ for every possible choice of $r$. Otherwise, if there is even one $i$ such that $a_i \neq b_i$, $p_a(r)=p_b(r)$ with probability at least $1 − (n − 1)/p$. (It can be proved by Schwartz-Zippel Lemma.)
The encoding is distance-amplifying: if $a$ and $b$ differ on even a single coordinate, then their encodings will differ on a $1−(n−1)/p$ fraction of coordinates. Due to the distanceamplifying nature of the code, checking equality of two vectors a and b was reduced to checking equality of a single (randomly chosen) entry of the encodings.